Вращение плоскости поляризации

Естественное вращение. Некоторые вещества, называемые оптически активными, обладают способностью вызывать вращение плоскости поляризации проходящего через них линейно поляризованного света. К числу таких веществ принадлежат кристаллические тела (например, кварц, киноварь), чистые жидкости (скипидар, никотин) и растворы оптически активных веществ в неактивных растворителях (водные растворы сахара, винной кислоты др.). Кристаллические вещества сильнее всего вращают плоскость поляризации в случае, когда свет распространяется вдоль оптиче-

ской оси кристалла. Угол поворота j пропорционален пути d, пройденному лучом в кристалле:

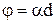(13.2)

Коэффициент a называют удельной постоянной вращения. Эта постоянная зависит от длины волны (дисперсия вращательной способности). В растворах угол поворота плоскости поляризации пропорционален пути света в растворе l и концентрации активного вещества с:

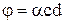(13.3)

Здесь a— величина, называемая удельной постоянной вращения. В зависимости от направления вращения плоскости поляризации оптически активные вещества подразделяются на п р а в о- и левовращающие. Направление вращения (относительно луча) не зависит от направления луча. Поэтому, если луч, прошедший через оптически активный кристалл вдоль оптической оси, отразить зеркалом и заставить пройти через кристалл еще раз в обратном направлении, то восстанавливается первоначальное положение плоскости поляризации. Все оптически активные вещества существуют в двух разновидностях — правовращающей и левовращающей. Существуют право и левовращающий кварц, право- и левовращающий сахар и т. д. Молекулы или кристаллы одной разновидности являются зеркальным отражением молекул или кристаллов другой разновидности (рис13.5).

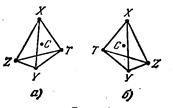
рис.13.5

Буквами С, X, Y, Z и Т обозначены отличающиеся друг от друга атомы или группировки атомов (радикалы). Молекула б является зеркальным отражением молекулы а. Если смотреть на тетраэдр, изображенный на рис13.5, вдоль направления СХ, то при обходе по часовой стрелке будет иметь место чередование ZYTZ для молекулы а и ZTYZ для молекулы б. То же самое наблюдается для любого из направлений CY, CZ и СТ. Чередование радикалов X, Y, Z, Чередование радикалов X, Y, Z, Т в молекуле б противоположно их чередованию в молекуле а. Поэтому, если, например, вещество, образованное молекулами а, правовращающее, то вещество, образованное молекулами б, будет левовращающим. Молекулы аминокислот, входящие в состав живых систем на Земле, оптически активны и все лево- вращающие. Поскольку строение молекул, особенно органических веществ, очень сложно, возникают возможности образования многих различных пар оптических изомеров.

Если между двумя скрещенными поляризаторами поместить оптически активное вещество (кристалл кварца, прозрачную кювету с раствором сахара и т. п.), то поле зрения просветляется. Чтобы снова получить темноту, нужно повернуть один из поляризаторов на угол j, определяемый выражением 13.2 или 13.3 В случае раствора, зная удельную постоянную вращения [a] данного вещества и длину I, можно, измерив, угол поворота j, определить по формуле 13.3 концентрацию раствора с. Метод имеет многочисленные приложения. В частности, им пользуются для нахождения концентрации сахара в производственных растворах и биологических объектах (кровь, моча).

Конечно, такие измерения должны проводиться в стандартных условиях опыта (l= const; t = const) в спектральной области, далекой от собственных полос поглощения исследуемого вещества, так как в противном случае наблюдаются некоторые аномалии. Угол поворота плоскости поляризации j можно измерить с большой точностью (погрешность измерений ~0,01°). Для достижения такой точности используют дополнительные устройства (полутеневые анализаторы), в которых измерение угла вращения проводят уравниванием освещенности двух половин поля зрения. Подобный способ значительно освещенности двух половин поля зрения. Подобный способ значительно точнее обычного определения, при котором нужно заметить исчезновение света, прошедшего через скрещенные поляризаторы.

Теория Френеля

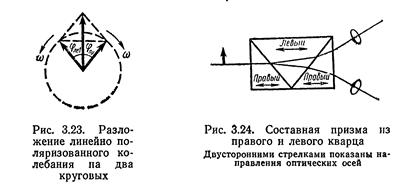
рис.13.6

а)

б)

рис.13.7

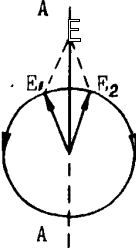
Интерпретация вращения плоскости поляризации была дана впервые Френелем, показавшим, что оно в какой-то степени аналогично двойному лучепреломлению. При изложении сущности формальной теории Френеля прежде всего установим, что любое линейно поляризованное колебание можно разложить на два круговых колебания с правым и левым вращением. Это ясно из геометрического построения, приведенного на рис. 13.6. Действительно, сумма двух векторов напряженности электрического поля E₁ и E₂ («левого» и «правого») равна удвоенной проекции любого из них на диаметр, т. е. вектору, направление которого постоянно, а модуль изменяется по периодическому закону с частотой w. Это и есть линейно поляризованное колебание. Френель предположил, что в оптически активном веществе скорость распространения волны с правым вращением отлична от скорости распространения волны с левым вращением, т. е. 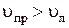. В силу этого все оптически активные вещества можно подразделить на «правые» ( 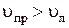) и «левые» ( 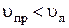). Для экспериментального доказательства справедливости этого предположения Френелем была построена специальная составная призма из «правого» и «левого» кварца (рис. 13.6б). Легко сообразить, что если 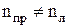, то при падении на такую призму линейно поляризованного света сначала пучок света раздваивается, а в последующем две поляризованные по кругу волны будут расходиться все больше и больше.

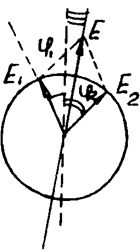
Рассмотрим, что произойдет с линейно поляризованной волной, распространяющейся в оптически активной среде. Разложим исходную волну Е на две, поляризованные по правому и левому кругу, скорости, распространения которых в данном веществе не равны. Очевидно, что время, необходимое каждой волне для прохождения одного и того же отрезка в исследуемой активной среде, окажется различным: 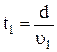и 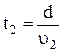. Следовательно, векторы Е₁ и Е₂ повернутся на различные углы j₁ и j₂. На рис. 13.7б, иллюстрирующем эти рассуждения, j₁ выбран больше, чем j₂. Для того чтобы результирующее колебание осталось линейно поляризованным, неизбежно должна повернуться плоскость симметрии.

Для определения направления колебаний в результирующей линейно поляризованной волне нужно сложить две поляризованные по кругу волны после прохождения ими равного пути в оптически активной среде, т. е. найти плоскость симметрии, которая (рис. 3.25) должна разделить пополам разность углов j₁ и j₂. Очевидно, что плоскость колебаний вектора Е в результирующей плоско поляризованной волне повернется по отношению к направлению, колебаний в исходной волне на угол j. Учитывая, что результирующий вектор Е на выходе из активного вещества должен составлять равные углы с векторами Е₁ и Е₂ можно записать 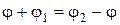. Откуда следует, что 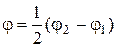. Так как

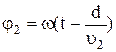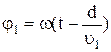, а , то

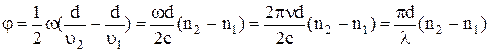
Сравнивая с 13.2 получаем удельная постоянная вращения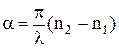

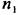, является показателем преломления волны с левой круговой поляризацией, а 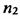— с правой. Отсюда заключаем, что для правовращающих

веществ 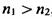, а для левовращающих 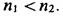Произведем теперь оценку величины 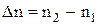, которую можно зафиксировать в опытах по вращению плоскости поляризации. Если точность измерения j « 0,01°( 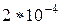рад), то при d « 10 см и l « 5 • 10^{-5 см можно измерить} Dn ~ 10^-9, т. е. обнаружить ничтожную разницу в показателях преломления 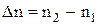. Итак, можно считать, что в рамках феноменологической электромагнитной теории света вращение плоскости поляризации получило объяснение. Однако эта теория не способна объяснить, почему скорость волны в правовращающем веществе отлична от ее скорости в левовращающем. Если попытаться ответить на этот вопрос с позиций молекулярной теории, то надо предположить, что вращение плоскости поляризации связано с асимметрией строения оптически активного вещества. В случае кристаллов главной причиной различия скоростей следует считать асимметрию внешней формы (отсутствие центра симметрии). Для аморфных однородных тел нужно связать исследуемое явление со строением сложных молекул активной среды.

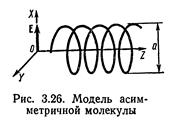Этот вопрос был подробно рассмотрен М. Борном 1915 г.), который показал, что описанный выше эффект можно объяснить, если учесть взаимодействие электромагнитного поля с веществом в пределах одной молекулы. При построении теории принималось во внимание, что все оптически активные вещества существуют в двух модификациях, характеризующихся правым и левым вращением плоскости поляризации, и рассматривались сложные асимметричные молекулы с пространственной структурой, не имеющие ни центра симметрии, ни плоскости симметрии. Наиболее простая модель этой молекулы — отрезок спирали. спирали. Пусть на такую молекулу, диаметр витка которой равен а, падает линейно поляризованная волна Е = Е_х (рис. 3.26). Она вызовет движение зарядов, направленное вдоль оси X. Но если заряды будут двигаться вдоль спирали, то неизбежно возникнет их движение и вдоль оси Y. Следовательно, можно говорить об Y -компоненте волны в веществе, наличие которой должно привести к отклонению плоскости колебаний от направления Е = Е_х. Расчет неизбежно должен быть связан с изменением фазы волны в пределах одной молекулы (вместо 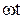нужно взять 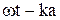), а его результат покажет, будет ли такое изменение существенно. На первый взгляд этот эффект кажется пренебрежимо малым, так как для оптической области отношение размера молекулы к длине волны порядка 10^-3, но возможность выявления в эксперименте чрезвычайно малых Dn не позволяет заранее отвергнуть подобное предположение.

Дисперсия света

ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН

С ВЕЩЕСТВОМ

Дисперсией света называются явления, обусловленные зависимостью показателя преломления вещества от длины световой волны. Эту зависимость можно охарактеризовать функцией

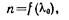
где 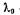— длина световой волны в вакууме. Дисперсией вещества называется производная n по l .Для всех прозрачных бесцветных веществ функция 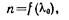имеет в видимой части спектра характер, показанный на рис. 142.1.

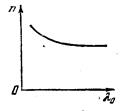
С уменьшением длины волны показатель преломления увеличивается со все возрастающей скоростью, так что дисперсия вещества dn/dl₀ отрицательна и растет по модулю с уменьшением l₀. Если вещество поглощает часть лучей, то ______-. в области поглощения и вблизи нее ход дис-

,%а Персии обнаруживает аномалию (см. рис.

Рис 142 ( 144.2). На некотором участке дисперсия веще-

ства dn/dko оказывается положительной. Та-

кой ход зависимости п от Ко называется аномальной дис-

персией.

Среды, обладающие дисперсией, называются дисперги-

рующими. В диспергирующих средах скорость световых волн

зависит от длины l₀ или частоты а.

Групповая скорость

Строго монохроматическая волна вида

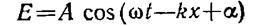(13.6)

представляет собой бесконечную во времени и в пространстве последовательность «горбов» и «впадин», перемещающихся вдоль оси Х с фазовой скоростью, которая описывает перемещение фазы в пространстве в единицу времени, т.е. 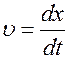,где x- расстояние между точками с одинаковыми фазами. Тогда

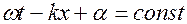(13.7)

Продифференцируем (13.7)

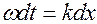, отсюда фазовая скорость зависит от частоты колебаний вектора напряженности электрического поля и волнового числа k

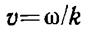(13/8)

С помощью гармонической волны нельзя передать никакого сигнала, так как каждый последующий «горб» ничем не отличается от предыдущего. Для передачи сигнала нужно на волне сделать «отметку», скажем, оборвав ее на некоторое время А/.

Однако в этом случае волна уже не будет описываться уравнением Dt.

Проще всего передать сигнал с помощью светового импульса (рис. 143.1).

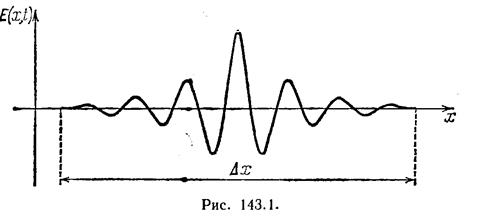
Согласно теореме Фурье подобный импульс можно представить, как наложение волн вида (13.6)), с частотами, заключенными в некотором интервале Dw. Суперпозиция волн, мало отличающихся друг от друга по частоте, называется волновым пакетом или группой волн. Аналитическое выражение для группы волн имеет вид

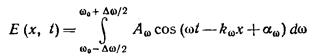(13.9)

(индекс w при A, k и a указывает на то, что эти величины для разных частот различны). При фиксированном t график функции 13.9 имеет вид, оказанный на рис. 143.1. С изменением t график смещается вдоль оси х. В пределах пакета плоские волны в большей или меньшей степени усиливают друг друга, вне пакета они практически полностью гасят друг друга. Соответствующий расчет дает, что чем меньше ширина пакета Dх, тем больший интервал частот Dw. или соответственно больший интервал волновых чисел Dk требуется для того, чтобы описать пакет с помощью выражения 13.9. Имеет место соотношение

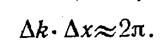
Подчеркнем, что для того, чтобы суперпозицию волн, описываемую выражением 13.9 можно было считать группой волн, необходимо соблюдение условия Dw.<w..

В недиспергирующей среде все плоские волны, образующие пакет, распространяются с одинаковой фазовой скоростью u. Очевидно, что в этом случае скорость движения пакета совпадает с u и форма пакета со временем не изменяется. Можно показать, что в диспергирующей среде пакет с течением времени расплывается — ширина его увеличивается. Если дисперсия невелика, расплывание пакета происходит не слишком быстро. В этом случае пакету можно приписать скорость u, под которой понимается скорость, с которой перемещается центр пакета, т. е. точка с максимальным значением Е. Эту скорость называют групповой скоростью. В диспергирующей среде групповая скорость и отличается от фазовой скорости u (имеется в виду фазовая скорость гармонической составляющей с максимальной амплитудой, иными словами — фазовая скорость для доминирующей частоты). Ниже мы покажем, что в случае, когда dn/dl<0 групповая скорость оказывается меньше фазовой (u <u); в случае, когда dn/dlo>0, групповая скорость больше фазовой ((u >u)).

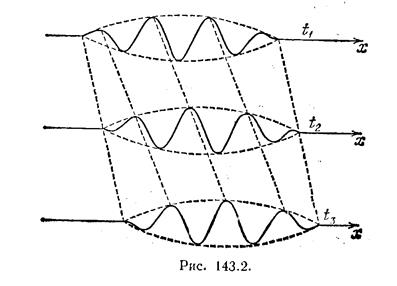
На рис. 143.2 показаны «фотографии» волнового пакета для трех последовательных моментов времени t₁, t₂ и t₃. Рисунок выполнен для случая, когда u<u. Из рисунка видно, что наряду с перемещением пакета происходит движение «горбов» и «впадин» «внутри» пакета, причем у левой границы пакета все время зарождаются новые «горбы», которые, пробежав вдоль пакета, исчезают у его правой границы. В результате, в то время как пакет в целом перемещается со скоростью u отдельные «горбы» и «впадины» перемещаются со скоростью u.

В случае, когда u>u направления перемещения пакета и движения «горбов» внутри него оказываются противоположными. Поясним сказанное на примере суперпозиции двух плоских волн с одинаковой амплитудой и разными длинами волн l.

На рис. 143.3 дана «моментальная фотография» волн. Одна из них изображена сплошной линией, другая — пунктирной. Интенсивность максимальна в точке А, где фазы обеих волн в данный момент совпадают. В точках B и С обе волны находятся в противофазе, вследствие чего интенсивность результирующей волны равна нулю. Допустим, что обе волны распространяются слева направо, причем скорость «сплошной» волны меньше, чем «пунктирной» (в этом случае 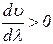, следовательно,

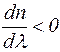Тогда место, в котором волны усиливают друг друга, будет со временем перемещаться влево относительно волн. В результате групповая скорость окажется меньше фазовой. Если скорость «сплошной» волны больше, чем «пунктирной» (т. е. dn/ 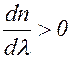место, в котором происходит усиление волн, будет перемещаться вправо, так что групповая скорость окажется больше фазовой.

Напишем уравнения волн, положив для упрощения формул начальные фазы равными нулю:

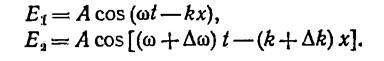
Здесь 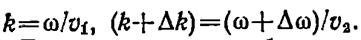,Пусть 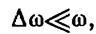соответственно 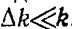Тогда, сложив колебания и произведя преобразования по формуле для суммы косинусов, получим

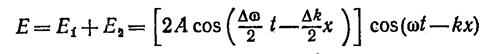(13.10)

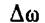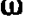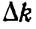(во втором множителе мы пренебрегли по сравнению с и по сравнению с k).

Множитель, стоящий в квадратных скобках, изменяется с х и t гораздо медленнее, чем второй множитель. Поэтому выражение (13.10) можно рассматривать как уравнение плоской волны, амплитуда которой изменяется по закону

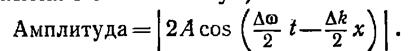
В данном случае имеется ряд одинаковых максимумов амплитуды, определяемых условием

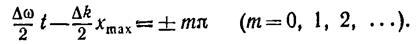(13.11)

Каждый из этих максимумов можно рассматривать как центр соответствующей группы волн.

Разрешив (13.11) относительно х_max получим

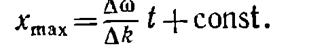
Отсюда следует, что максимумы перемещаются со скоростью

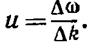
Полученное выражение представляет собой групповую скорость для случая, когда группа образована двумя составляющими.

Групповой пакет неизбежно деформируется. Если эта деформация осуществляется медленно, то полученные закономерности приближенно выполняются. Более точная формулировка условий существования недеформируемой группы волн предполагает наличие узкого спектра синусоидальных волн, образующих группу, и определенных свойств среды, в которой происходит ее распространение [отсутствие резких изменений n(l) вблизи l₀]. При нарушении этих условий импульс быстро деформируется («расползается») и описание движения его как целого становится неточным.

Итак, групповая скорость 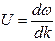, тогда как фазовая скорость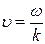

Найдем связь между фазовой и групповой скоростями,

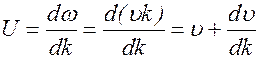
Это выражение легко преобразовать, учитывая, что

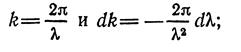
тогда окончательно получается выражение, называемое формулой

Рэлея:

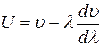
Проведем подробный анализ найденного соотношения между фазовой и групповой |скоростями.

1. Если 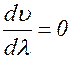т. n = const, то дисперсия отсутствует и 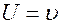иными словами, фазовая и групповая скорости совпадают. Это справедливо не только для вакуума, но и для некоторых материальных сред. В частности, для световых волн в воздухе и воде можно не учитывать дисперсии, так как она пренебрежимо мала

2. Если 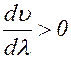., то 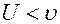. Этот случай, как правило, реализуется при прохождении света через различные стекла и другие прозрачные среды. Заметим, что если 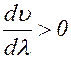, то 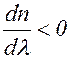, то так как

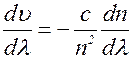
Следовательно, показатель преломления n уменьшается с увеличением длины волны. Эту часто встречающуюся зависимость n от l называют нормальной дисперсией.

3. Если 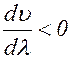, то U> u. В этом случае 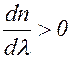, т. е. показатель преломления возрастает с увеличением длины волны. В дальнейшем будет показано, что такая зависимость n от l может иметь место в тех областях спектра, где наблюдается интенсивное поглощение света. Она называется аномальной дисперсией.

Заключение

Необходимо помнить, что вид поляризации зависит от разности фаз, колебаний взаимодействующих световых векторов. По Френелю линейно поляризованный свет можно представить как совокупность двух волн, имеющих правую и левую круговую поляризацию. Скорость распространения этих волн в средах, имеющих ассиметричные молекулы, различна, поэтому между этими волнами возникнет разность фаз. Чтобы результирующая волна по-прежнему оставалась линейно поляризованной, необходимо чтобы результирующий вектор напряженности электрического поля испытал поворот относительно своего первоначального положения. Поворот плоскости поляризации в оптических средах дает возможность исследовать структурную формулу вещества, измерять концентрацию оптически активных веществ в растворе. С помощью поляризованного света изучают структуру и свойства различных веществ, причем в ряде случаев эти методы оказываются значительно чувствительнее методов рентгеноструктурного анализа. С помощью поляризованного света исследуют межмолекулярные взаимодействия, в частности перенос энергии возбуждения между молекулами в растворах и кристаллах. Биохимики определяют детали структуры белков, аминокислот и отдельных элементов клетки.