Угловая ширина главных максимумов

Определим угловую ширину центрального максимума. С обеих сторон он ограничен добавочными минимумами. Таким образом, при переходе из главного максимума в соседний минимум разность хода Δ=dsinθ должна измениться на λ/N. Из этого условия можно оценить угловую полуширину δθ главных максимумов: 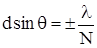Отсюда полуширина центрального максимума определиться углом дифракции, при котором наблюдается добавочный минимум

Ширина центрального максимума

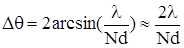(10.14)

Заметим, что Nd- длина дифракционной решетки, т.е. угловая ширина центрального дифракционного максимума определяется длиной дифракционной решетки.

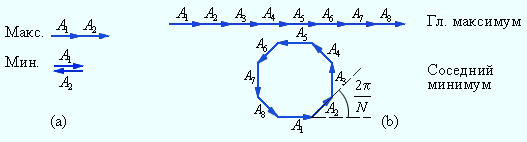
Рисунок 10.7. Сложение колебаний в максимуме и минимуме интерференционной картины: a – интерференция двух волн, b – интерференция N волн (N = 8).

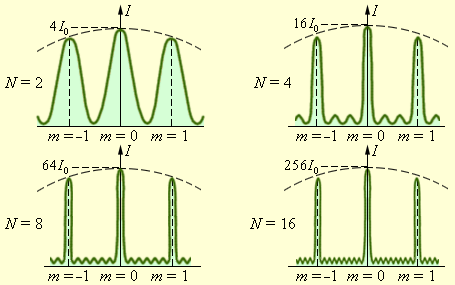
Можно сделать важный вывод: главные максимумы при дифракции света на решетке чрезвычайно узки. Рис. 10.8 дает представление о том, как меняется острота главных максимумов при увеличении числа щелей решетки.

Рисунок 10.8. Распределение интенсивности при дифракции монохроматического света на решетках с различным числом щелей. I0 – интенсивность колебаний при дифракции света на одной щели.

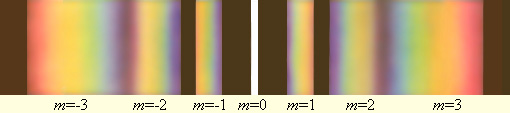
Как следует из формул, описывающих спектр дифракционной решетки, положение главных максимумов (кроме нулевого) зависит от длины волны λ. Поэтому решетка способна разлагать излучение в спектр, то есть она является спектральным прибором. Если на решетку падает немонохроматическое излучение, то в каждом порядке дифракции (т. е. при каждом значении m) возникает спектр исследуемого излучения, причем фиолетовая часть спектра располагается ближе к максимуму нулевого порядка. На рис.10.9 изображены спектры различных порядков для белого света. Максимум нулевого порядка остается неокрашенным.

Рисунок.10.9. Разложение белого света в спектр с помощью дифракционной решетки.