Решение гидродинамической части задачи (решение Блазиуса)
Точное решение уравнения движения в приближении пограничного слоя получено Блазиусом при использовании автомодельных переменных.
Уравнение движения
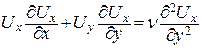 . .
| (9.13) |
Запишем в переменных Блазиуса:
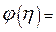 ; ; 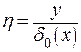 . .
| (9.14) |
Запишем
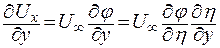 . .
| (9.15) |
Так как
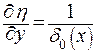 , ,
| (9.16) |
то
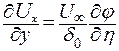 . .
| (9.17) |
Запишем
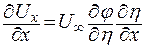 . .
| (9.18) |
Так как
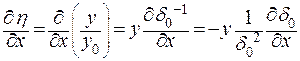 , ,
| (9.19) |
тогда:
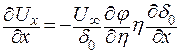 . .
| (9.20) |
Найдем 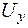 из уравнения неразрывности:
из уравнения неразрывности:
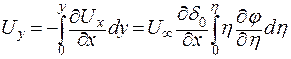 . .
| (9.21) |
Возьмем вышеуказанный интеграл по частям:
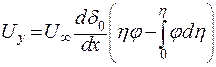 . .
| (9.22) |
После подстановки 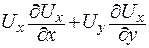 в исходное уравнение получим
в исходное уравнение получим
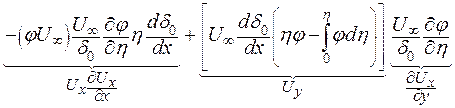
| (9.23) |
После сокращения получим:
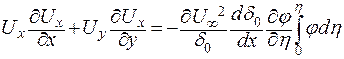 . .
| (9.24) |
Правая часть исходного уравнения движения запишется как
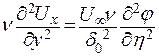 . .
| (9.25) |
Таким образом уравнение движения в переменных Блазиуса:
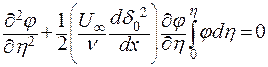 . .
| (9.26) |
Введем условие для выбора 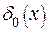 .
.
Будем считать, что 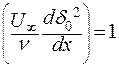 , откуда
, откуда 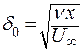 .
.
Значит, переменная Блазиуса может быть записана как
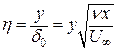 . .
| (9.27) |
Окончательное уравнение движения:
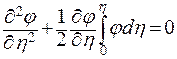 . .
| (9.28) |
Решается при граничных условиях
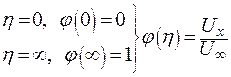
|
Перейдем от интегро-дифференциального уравнения к дифференциаль- ному уравнению более высокого порядка вводя функцию 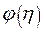 как:
как:
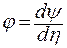 или или 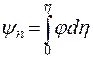
| (9.29) |
и положим 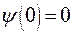 , тогда получаем дифференциальное уравнение Блазиуса третьего порядка
, тогда получаем дифференциальное уравнение Блазиуса третьего порядка
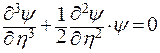
| (9.30) | |
с граничными условиями 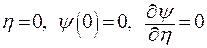 ; ;
| ||
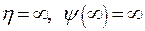 . .
| ||
Уравнение нелинейное, поэтому нет решений в классе обыкновенных функций. Блазиус решал уравнение в форме рядов и получил:
| 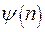
| 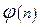
| 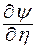
|
| 0,33206 | |||
| 0,16557 | 0,32979 | 0,32301 | |
| 0,65003 | 0,62977 | 0,26675 | |
| 1,39682 | 0,84605 | 0,16136 | |
| 2,30576 | 0,95552 | 0,06424 | |
| 3,28329 | 0,99155 | 0,01591 | |
| 
|
Заметим, что при 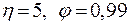 , то есть
, то есть 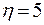 является границей пограничного слоя. Отсюда:
является границей пограничного слоя. Отсюда:
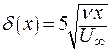 . .
| (9.31) |
Касательное напряжение вязкого трения равно:
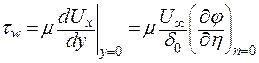 . .
| (9.32) |
Т.к. 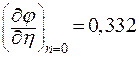 , то:
, то:
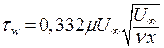 . .
| (9.33) |
Касательное напряжение часто записывают через коэффициент трения Cf:
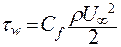 . .
| (9.34) |
Сопоставляя эти два соотношения, получим закон Блазиуса:
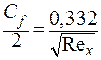 . .
| (9.35) |
Значения теплового и гидродинамического слоев связаны соотношением:
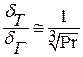 . .
| (9.36) |
Ранее мы получили 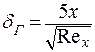 , тогда:
, тогда:
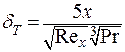 . .
| (9.37) |
Для капельных жидкостей 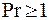 , следовательно
, следовательно 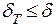 , то есть выполняется условие, принятое при интегрировании. Для жидких металлов
, то есть выполняется условие, принятое при интегрировании. Для жидких металлов 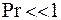 тогда
тогда 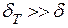 и полученные результаты неприемлемы. Для газов
и полученные результаты неприемлемы. Для газов 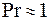 (хотя
(хотя 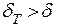 ) опыт показывает, что результат приемлем.
) опыт показывает, что результат приемлем.
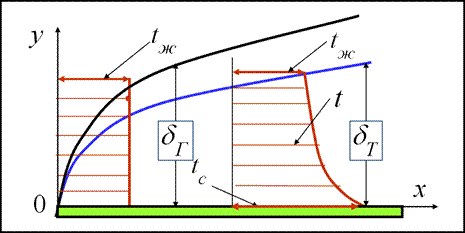
Получим соотношение для теплоотдачи вида 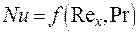 . Из решения тепловой задачи обтекания пластины было получено соотношение для расчета коэффициента теплоотдачи:
. Из решения тепловой задачи обтекания пластины было получено соотношение для расчета коэффициента теплоотдачи:
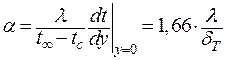 . .
| (9.38) |
Вводя 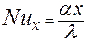 и подставляя расчетное значение α и δТ, окончательно получим
и подставляя расчетное значение α и δТ, окончательно получим
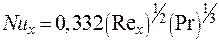 . .
| (9.39) |
Дата добавления: 2017-10-04; просмотров: 3044;











