Закон сохранения массы для движущейся жидкости

Объем жидкости или газа, проходящий в единицу времени через живое сечение потока (трубки тока), называется объемным расходом жидкости или газа.

Для элементарной струйки элементарный объемный расход:

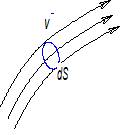
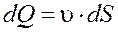. (19)

Для трубки тока конечного поперечного сечения скорости в разных точках сечения могут быть различными.

В этом случае объемный расход через трубку тока определяется интегралом:

.

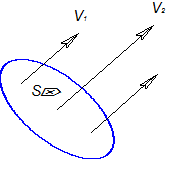
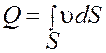Средняя скорость жидкости или газа в живом сечении потока определяется по формуле:

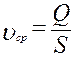. (20)

Или:

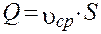. (21)

Массовый расход жидкости или газа через поперечное сечение потока равен:

. (22)

Если плотность постоянна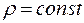

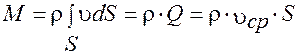. (23)

Размерности: ; ; .

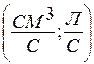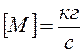Закон сохранения массы для потока жидкости или газа выражается в том, что поток массы, т.е. масса жидкости или газа, проходящая в единицу времени через сечение потока, является величиной постоянной вдоль потока, т.е.

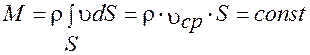. (24)

Для двух сечений 1 – 1 и 2 – 2 выражение (24) записывается в виде:

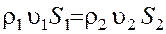, (25)

где 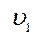, 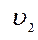– средние скорости в соответствующих сечениях.

Выражение (25) называется уравнением неразрывности или уравнением расхода для одномерного движения жидкостей и газов.

Для несжимаемой жидкости и закон сохранения массы для одномерного потока (24) записывается в виде:

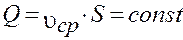. (26)

т.е. при одномерном течении несжимаемой жидкости постоянным вдоль потока будет не только массовый, но и объемный расход.

Для двух сечений 1–1 и 2 – 2 выражение (26) записывается в виде:

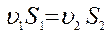. (27)

Выражение (27) называется уравнением неразрывности или уравнением расхода для одномерного движения несжимаемой жидкости.

Из уравнения (10) можно получить следующую связь между скоростью жидкости и площадью поперечного сечения потока:

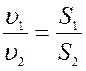. (28)