Корпускулярно-волновая природа электрона

В 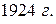французский физик Луи де Бройль предположил, что двойственной природой (корпускулярно-волновой) обладают не только фотоны-частицы света, но и электроны. Он исходил из следующего.

Так как оба уравнения

,

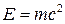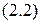
– уравнение Эйнштейна, связывающее массу и энергию фотона,

,

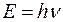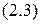
– уравнение Планка, связывающее энергию фотона и частоту излучения, относятся к одному и тому же объекту, то их можно приравнять. Тогда

.

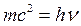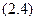
Напомним, что в физике произведение массы 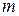на скорость движения частицы 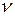называют количеством движения или импульсом 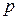. Следовательно, для фотона 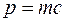и уравнение 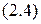перепишем в виде

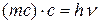
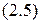
или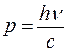

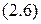
Поскольку для любого волнового процесса частота 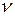, длина волны 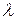и скорость распространения волны u связаны соотношением

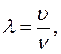
откуда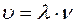

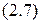
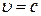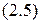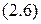В частном случае для фотона . Тогда из и получим

,

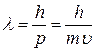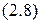
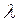– длина волны электрона или длина волны де Бройля.

Например, для тела массой 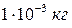, имеющего скорость 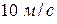, длина волны де Бройля 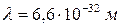, т.е. зафиксировать такую волну даже с помощью самых совершенных приборов невозможно. Другое дело электрон, имеющий массу покоя 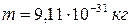и скорость движения по орбите 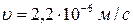, для него или 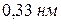. А это уже порядок размеров атомов.

Открытие волновых свойств микрочастиц означало, что законы движения в микромире принципиально отличаются от привычных законов классической механики. Корпускулярно-волновая природа электрона, которая следует из уравнения Луи де Бройля 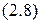, связывающего массу частицы (корпускулярное свойство) с длиной волны (волновое свойство), свидетельствует о том, что на ряду со свойствами частицы (масса покоя, траектория и направление движения и др.) микрочастицы обладают и свойствами электромагнитного поля. Иначе говоря, с каждым движущимся электроном связан волновой процесс. В связи с этим частица с различной вероятностью, но одновременно может быть обнаружена в любой точке пространства, где происходит движение рассматриваемой волны. Рисунок 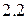демонстрирует вышеизложенное.

Если движущийся электрон в гипотетическом эксперименте удалось бы сфотографировать при его движении вокруг ядра через малые промежутки времени, то полученная картина напоминала бы облако, плотность которого неодинакова в объеме (рис. 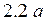). Очевидно, облако окажется наиболее плотным там, где выше вероятность нахождения электрона. Изменение электронной плотности с расстоянием 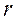обычно изображается в виде кривой радиального распределения вероятности (рис. 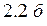). Эта кривая показывает, что нахождение электрона наиболее вероятно в оболочке радиуса .

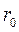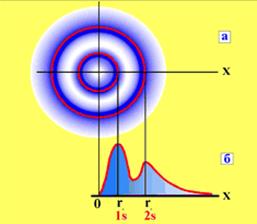
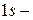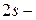Рисунок 2.2. Распределение электронной плотности на и орбиталях: а) электронное облако атома с неравномерной плотностью; б) радиальное распределение вероятности для 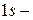орбитали атома водорода.

Новое представление об электроне заставило физиков отказаться от принятой модели атома, в которой электрон движется по определённым траекториям или орбитам. Поскольку электрон, обладая свойствами электромагнитной волны, движется по всему атомному объему, образуя электронное облако, плотность которого в той или иной части занимаемого пространства не одинакова, то оно получило название атомной орбитали (общепринятое сокращение 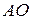). Таким образом, атомная орбиталь – это пространство вблизи ядра атома, в котором вероятность пребывания электрона наибольшая. Поверхность, ограничивающая вероятности нахождения электрона или электронной плотности, называют граничной. Атомная орбиталь и плотность электронного облака имеют одинаковую граничную поверхность (форму) и одинаковую пространственную ориентацию.

Двойственную природу электрона и других элементарных частиц удалось объяснить немецкому физику В. Гейзенбергу с помощью принципа неопределённости: невозможно в любой данный момент времени определить сколь угодно точно и положение частицы в пространстве, и её скорость (импульс).Это обусловлено тем, что измерения проводятся каким-либо прибором, который фиксирует взаимодействие электрона с носителем этой информации, например, фотоном или другой частицей. Следовательно, неминуемо происходит взаимодействие этих частиц, хотя бы посредством их электромагнитных полей, а это приводит к тому, что существенно изменяется или положение электрона, или его скорость и её направление.

Количественно это соотношение может быть записано в виде:

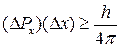
Здесь 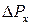– неопределённость в величине импульса, направленного вдоль оси ; 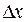– неопределённость в положении частицы вдоль этой же координаты. Отсюда вытекает, что чем точнее определено положение частицы в пространстве 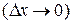, тем больше неопределённость его импульса, т.е. скорости. Кроме того, энергия микрочастицы ни при каких условиях не может быть равна нулю, так как при 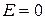её координаты и импульс были бы точно известны, это противоречит принципу неопределённости. Таким образом, движение микрочастиц в системе не может прекратиться даже при абсолютном нуле температур.

Новый раздел физики и химии, который изучает явления, происходящие в микромире, получил название квантовой или волновой механики. Основой её служит уравнение Э. Шредингера, учитывающее не только все взаимодействия электронно-ядерных систем, но и волновые свойства электронов. Однако точное решение удалось получить только для атома водорода или водородоподобных ионов, для многоэлектронных систем необходимо использовать различные приближения. Таким образом, для полной характеристики электрона в атоме оказалось достаточным иметь четыре параметра – квантовые числа, три из которых характеризуют пространственное распределение электрона в атомной орбитали, и вытекают из решения уравнения Шредингера.

Квантовые числа

1. Главное квантовое число 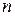характеризует:

- число энергетических уровней в атоме;

- энергию электрона на данном энергетическом уровне;

- размер атома.

В общем случае 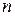принимает значения от 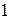до 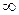. В невозбуждённых атомах, т.е. таких, состояние которых соответствует их расположению в периодической системе элементов Д. И. Менделеева, 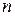изменяется от 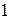до 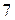в соответствии с числом периодов в периодической системе. Чем меньше 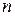, тем больше энергия взаимодействия электрона с ядром. Например, при 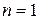атом водорода находится в основном состоянии, при 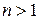– в возбуждённом.

В многоэлектронных атомах электроны с одинаковыми значениями 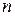образуют слой или уровень обозначаемый буквам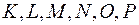и и 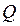. Буква 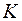соответствует первому уровню, 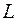– второму и т.д.

2. Орбитальное или побочное квантовое число 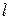характеризует:

– Энергию электрона на энергетическом подуровне.

На уровне может находиться много электронов (максимально 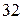), но не все они обладают одинаковой энергией. В результате взаимного отталкивания электронов происходит расщепление энергетического уровня на подуровни (рисунок ).

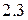Рисунок 2.3 Расщепление энергетического уровня на подуровни

Те электроны, которые принадлежат одному и тому же подуровню, т.е. электроны с одинаковыми значениями 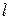, обладают одинаковой энергией. Такое состояние называют вырожденным по энергии.

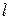принимает значения от 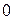до 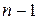, но это правило справедливо для невозбуждённых атомов для 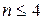. Кроме числовых значений, 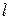имеет и буквенные обозначения:

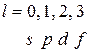
Так, при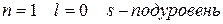

,

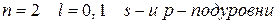
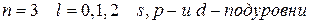
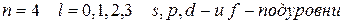т.е. число энергетических подуровней в пределах данного энергетического уровня;

- Форму атомных орбиталей (рисунок ).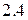

3. Магнитное квантовое число 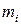определяет:

- ориентацию атомных орбиталей в пространстве;

- число атомных орбиталей на энергетическом подуровне.

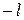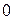принимает целые значения от через до 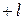, т.е. 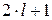значений. Например, рассмотрим подуровень, для него 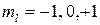– всего 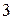значения. Следовательно, число 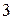означает, что на данном энергетическом подуровне находится три атомных орбитали, различным образом ориентированных в пространстве (рисунок ).

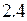Вышеизложенное можно представить в виде таблицы .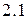

Таблица 2.1 - Число орбиталей на энергетических подуровнях

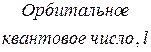
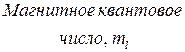
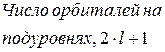
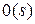
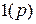
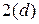
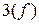
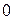
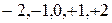
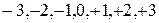
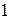
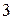
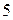
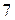
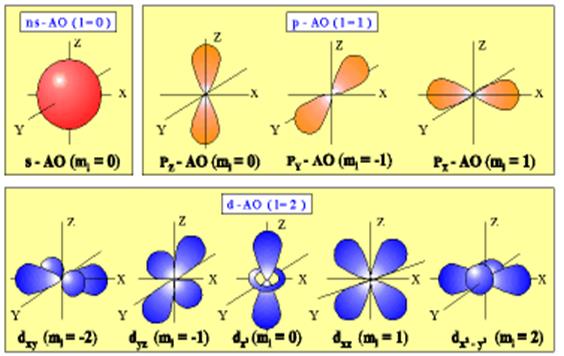
Рисунок 2.4. Конфигурации атомных орбиталей и ориентация их в пространстве

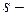орбитали сферически симметричны для любого n и отличаются друг от друга только размерами сферы.

орбитали существуют при 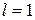, поэтому возможны три варианта ориентации в пространств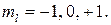е: Все орбитали обладают узловой плоскостью, делящей орбиталь на две области, поэтому граничные поверхности имеют форму гантелей, ориентированных в пространстве под углом 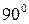друг относительно друга. Осями симметрии для них являются координатные оси, которые обозначаются .

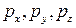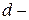орбитали определяются квантовым числом , при котором то есть характеризуются пятью вариантами ориентации в пространстве. 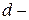орбитали, ориентированные по осям координат, обозначаются 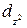и 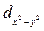, а ориентированные по биссектрисам координатных углов -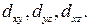

Семь 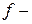орбиталей, соответствующих 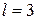, имеют ещё более сложную конфигурацию и на рисунке 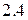не показаны.

4. Спиновое квантовое число 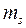(от английского 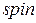– вращение) упрощено можно представить как описывающее вращение электрона вокруг собственной оси по часовой стрелке и против, поэтому оно имеет только два значения 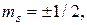представляющие собой две проекции углового момента электрона на выделенную ось.

Для изображения атомной орбитали и электронов часто используют «квадратики» и «стрелки», направленные вверх или вниз. Два электрона с одинаковыми значениями квантовых чисел 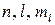, но с противоположно направленными спинами, называются спаренными или неподелённой электронной парой и обозначаются , неспаренные электроны – или .

Итак, четыре квантовые числа описывают состояние электрона в атоме и характеризуют энергию электрона, его спин, форму электронного облака и его ориентацию в пространстве. При переходе атома из одного состояния в другое происходит перестройка электронного облака, то есть изменяются значения квантовых чисел, что сопровождается поглощением или испусканием атомом квантов энергии.