Равновесие в тройных системах. 3-х угольная диаграмма Гиббса

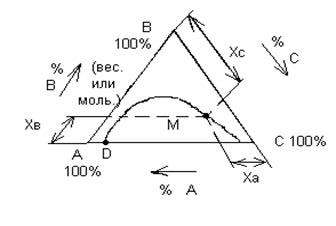
Общий состав 3-х компонентной смеси на диаграмме Гиббса изобразится точкой М с координатами Х_А, Х_В, Х_С, вершины треугольника соответствуют чистым компонентам.

Рассмотрим равновесные соотношения в системе ж. – ж.

Пусть система состоит из 3-х компонентов А, В, С при t = const. Причём В растворим в А и С во всех соотношениях, а А и С ограниченно растворимы друг в друге. Область взаимной растворимости

компонентов ограничивается так называемой бинодальной кривой ДКР (строится по экспериментальным справочным данным).

Эта кривая выражает равновесное распределение компонента В в А и С. Точки под кривой находятся в области расслоения жидкостей А и С; над – в области полной растворимости. Для 3-х компонентной смеси (точка М) можно определить составы расслаивающихся жидкостей, соответствующих равновесному насыщению. Они лежат на пересечении хорды равновесия RE с бинодальной кривой. RE – хорда равновесия, одна из бесконечно возможных. Для построения хорды используют опытные данные из справочной литературы. Все смеси вдоль RE образуют два жидких слоя. Используя правило рычага, можно определить количества смесей. Правило рычага: состав смеси (точка М), получаемый при смешении 2-х других смесей (R и E), лежит на прямой, соединяющей составы этих смесей, в точке, делящей эту прямую на отрезки, обратно пропорциональные количествам смесей. То есть, если известны количество и состав исходной смеси (точка М) по известным составам экстракта Е и рафината R можно определить количества экстракта и рафината. Обозначим G_E - количество экстракта, G_R – количество рафината. G_M – количество исходной смеси.

GM = GR +GE

Уравнение мат. баланса: ; по правилу рычага: .Коэффициент распределения: - К – коэффициентом распределения одного из компонентов системы (например, В) называется отношение К = концентрация В в фазе Е / концентрация В в фазе R; (концентрации мольные или весовые); К может быть >, <, = 1.

К не имеет постоянного значения, поскольку зависит от состава фаз.