Тема 4. Момент инерции твердого тела. Теорема Штейнера
Моментом инерции материальной точкимассой m относительно некоторой оси вращения называется физическая величина I, равная произведению массы этой материальной точки на квадрат расстояния 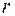 от этой точки до данной оси вращения:
от этой точки до данной оси вращения:
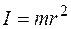 .
.
Для того, чтобы найти момент инерции твердого тела относительно некоторой оси вращения, необходимо разбить это тело на элементарные объемы так, чтобы каждый элементарный объем можно было рассматривать как материальную точку массой 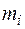 , находящуюся на определённом расстоянии
, находящуюся на определённом расстоянии 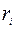 от данной оси вращения. Тогда момент инерции твердого тела I равен суммемоментов инерции всех n материальных точек массами
от данной оси вращения. Тогда момент инерции твердого тела I равен суммемоментов инерции всех n материальных точек массами 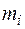 , на которые разбито это тело, или сумме произведений масс материальных точек
, на которые разбито это тело, или сумме произведений масс материальных точек 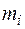 на квадраты расстояний
на квадраты расстояний 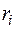 от этих материальных точек до рассматриваемой оси:
от этих материальных точек до рассматриваемой оси:
 .
.
В качестве примера найдем момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно оси, перпендикулярной основанию цилиндра и проходящей через его центр масс (рис. 4).
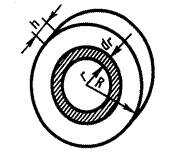 Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним (r+dr). Так как dr<<r , то считаем, что расстояние всех точек полого цилиндра от оси равно r. Поэтому момент инерции каждого полого цилиндра можно Рис. 4
Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним (r+dr). Так как dr<<r , то считаем, что расстояние всех точек полого цилиндра от оси равно r. Поэтому момент инерции каждого полого цилиндра можно Рис. 4
определить следующим образом:
dI=r2dm ,
где dm – масса элементарного полого цилиндра, равная rdV
(r — плотность материала, dV – объем полого цилиндра, равный 2prhdr).
Тогда момент инерциии элементарного полого цилиндра dI=2prhr3dr.
Следовательно, момент инерции сплошного цилиндра
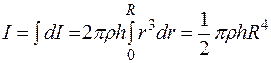 .
.
Так как pR2h — объем сплошного цилиндра, а prhR2 — его масса, то момент инерции сплошного цилиндра: 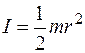 .
.
Теорема Штейнера. Если известен момент инерции тела 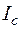 относительно оси ОО′, проходящей через центр масс тела, то момент инерции этого же тела относительно другой оси
относительно оси ОО′, проходящей через центр масс тела, то момент инерции этого же тела относительно другой оси 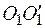 , параллельной оси ОО′, равен сумме момента инерции
, параллельной оси ОО′, равен сумме момента инерции 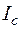 и произведения массы т данного тела на квадрат расстояния а между этими осями ОО′ и
и произведения массы т данного тела на квадрат расстояния а между этими осями ОО′ и 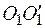 , то есть:
, то есть:
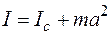 .
.
Дата добавления: 2017-10-04; просмотров: 1425;











