Расчётные соотношения для неуправляемых выпрямителей

Неуправляемый выпрямитель характеризуется рядом показателей к которым относятся, выходное напряжение – U ₀, коэффициент пульсаций – К_П, частота первой гармоники пульсаций – f_п, коэффициент выпрямления и др. Найдём эти показатели для разных схем выпрямления.

Простейший выпрямитель (рис. 3.15, пульсность р=1). Форма выходного напряжения приведена на рис. 3.24а.

Мгновенное напряжение U_d на интервале 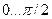подчиняется закону косинуса (повторяет напряжение U₂)

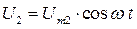(3.9)

Среднее значение выходного напряжения равно

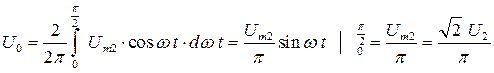. (3.10)

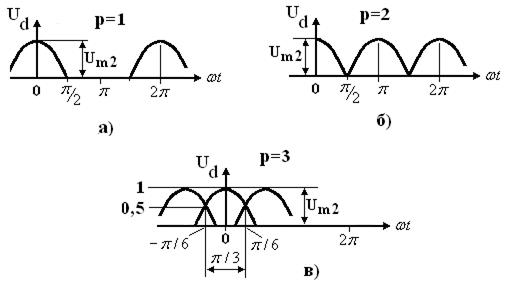
Рисунок 3.24 – Выходное напряжение при разной пульсности

Отношение

(3.11)

называют коэффициентом выпрямления. Он показывает степень использования трансформатора. Для нашего случая

(3.12)

т.е. довольно низкая величина.

Найдём теперь коэффициент пульсаций по первой гармонике.

Если грубо принять напряжение U_d гармоническим и считать, что его амплитуда 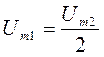, то 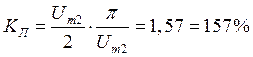. Поэтому, такие схемы без сглаживающих фильтров не используют.

Обратное напряжение на вентиле равно U_обр = U_m2.

Для двухфазной однотактной схемы (рис. 3.17 пульсность р=2).

Среднее значение (постоянная составляющая) выходного напряжения (рис.3.24 б) равно

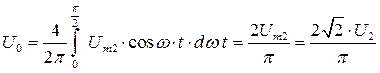(3.13)

Коэффициент выпрямления равен

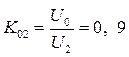(3.14)

Если грубо принять напряжение U_d гармоническим и считать, ч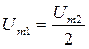то , то . Если же периодическую кривую напряжения Ud разложить в ряд Фурье и выделить первую гармонику, то получим К_П = 0,667. Это соответствует аналитическому выражению

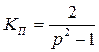, (3.15)

которое справедливо при . Частота первой гармоники пульсаций кратна частоте сети

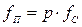
Приведённые соотношения действительны и для мостовой схемы (рис.3.18), поскольку их пульсности одинаковы (р=2). Различными в этих схемах будут обратные напряжения на вентилях, которые соответственно равны:

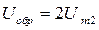для р = 2*1 = 2 (3.16)

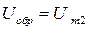для р = 1*2 = 2 (мостовая схема).

Для трёхфазной однотактной схемы (рис. 3.19 пульсность р=3). Форма выходного напряжения приведена на рис. 3.24 в.

Среднее значение выходного напряжения (рис.3.24в) равно

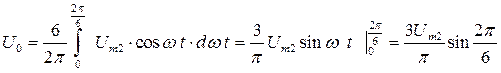(3.17)

Получилась универсальная формула, справедливая при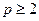

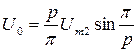(3.18)

Если р =2, то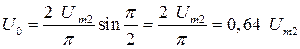

Если р =3, то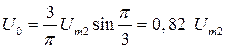

Коэффициент выпрямления равен

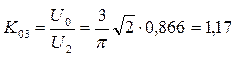(3.19)

Что существенно выше, чем в предыдущих схемах.

Если считать, что пульсации гармонические и их двойная амплитуда

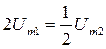, откуда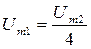

тогда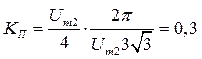

При точном разложении напряжения U_d на гармоники, согласно выражению (3.15) получаем К_П = 0,25.

Обратное напряжение на вентиле равно линейному:

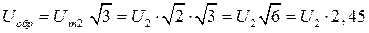(3.20)

Для трёхфазной двухтактной схемы (рис. 3.21 пульсность р=6) получаем:

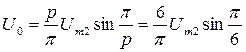(3.21)

В схеме выпрямления вторичные обмотки включены звездой, поэтому U_m2 следует умножить на .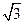

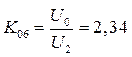(3.22)

К_П = 0,057

При включении вторичных обмоток треугольником множитель 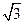не нужен и 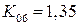. Видно, что с ростом пульсности, растёт коэффициент использования трансформатора и уменьшается коэффициент пульсаций. Поэтому схема Ларионова получила широкое распространение в преобразовательной технике.

В 12- пульсной схеме выпрямления, которая приведена на рис. 3.23 коэффициент пульсаций составляет всего 1,4% и поэтому она может применяться без сглаживающего фильтра.