Расчет на внецентренное сжатие

Внецентренное сжатие является наиболее распространенным видом напряженного состояния каменных конструкций. Эксперименты на внецентренно сжатых образцах кладки показали:

1. Фактическое разрушающее усилие в 1,5-2 раза больше полученного теоретического по формулам сопромата как для упругого материала. Отчасти такое расхождение можно объяснить криволинейностью эпюры напряжений в отличие от прямолинейной эпюры напряжений, принимаемой как для упругого материала с постоянным модулем упругости.

2. В момент разрушения деформации кладки при внецентренном сжатии значительно больше, чем при центральном сжатии. Это
отчасти объясняется тем, что менее напряженная часть сечения в
какой-то мере помогает работе более напряжённой части и происходит перераспределение напряжений благодаря пластическим деформациям кладки.

3. При значительных эксцентриситетах ( 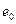) приложения нагрузки N (рис.25) в растянутой зоне возникнут трещины, что приведет к изменению работы сечения. Если трещина глубиной С, то нетрудно видеть, что величина эксцентриситета е₀ уменьшится и станет равной:

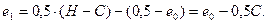(11)

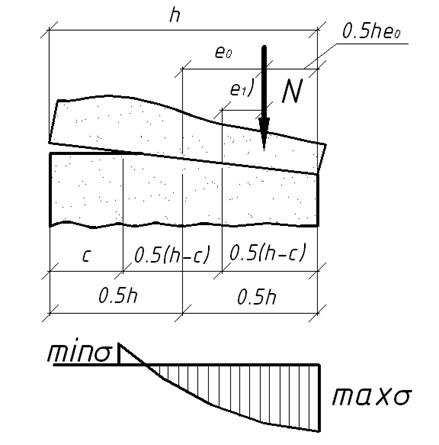
Рис. 25. Приложение силы N при внецентренном сжатии

Если в этом выражении принять 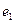=0, то получим, что 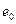= 0,5С, то есть при раскрытии трещины до величины С = 2• 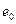действующая нагрузка N будет центральной по отношению к оставшемуся сечению.

При раскрытии трещины происходящее уменьшение момента сказывается больше, чем уменьшение сечения по мере образования трещин. Этим обстоятельством и объясняется некоторое возрастание несущей способности элемента до определенного предела после раскрытия трещины, так как создается более равномерное распределение напряжений по сечению за счет уменьшения эксцентриситета приложения нагрузки к оставшемуся сечению. Такое явление свойственно только внецентренному сжатию, так как при поперечном изгибе первая трещина уменьшает сечение, но не уменьшает момент, и поэтому сечение разрушается.

4. Специальные эксперименты позволили определить зависимость между эксцентриситетами (е₀) приложения силы, расстоянием от более сжатой грани сечения до центра тяжести сечения (у) и величиной раскрытия швов кладки. На основании этих опытов нормами принят предельный эксцентриситет (е_0,пр=0,7•У), при достижении которого требуется производить расчет по раскрытию трещин. На основании экспериментальных исследований приняты следующие допущения при расчете кладки на внецентренное сжатие:

- расчет исходит из условия равновесия между внешней расчетной силой (N) и прямоугольной эпюрой сжимающих напряжений взамен действительной криволинейной эпюры, как показано на рис. 26;

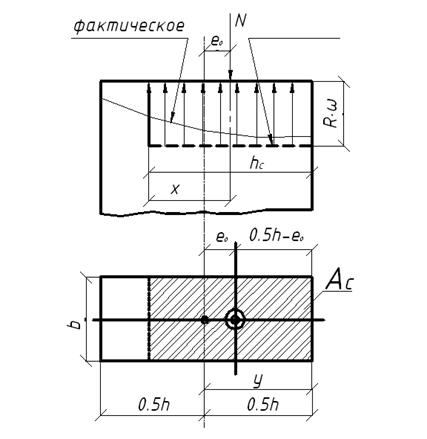
Рис. 26. Равновесие между внешней расчетной силой (N) и прямоугольной эпюрой сжимающих напряжений взамен действительной криволинейной эпюры

- размер эпюры сжимающих напряжений d принимается таким, чтобы центр тяжести сжатой зоны А_с совпадал с точкой приложения внешней сжимающей силы N.

В этом случае, когда центр тяжести сжатой зоны сечения совпадает с осью приложения внешней нагруз­ки, расчет внецентренно сжатого сечения сведется к расчету на центральное сжатие части этого сечения А_с по формуле:

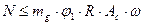(12)

где 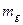и R - те же значения, что и в выражении (2); 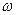- коэффициент полноты эпюры, определяемый по экспериментальным формулам; 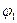- коэффициент продольного изгиба, определяемый по экспериментальной формуле; А_с - площадь сжатой части сечения при прямоугольной эпюре напряжений; положение границы сжатой площади А_с определяется из условия равенства нулю статического момента этой площади относительно ее центра тяжести.

Например, для прямоугольного сечения в обозначениях, принятых на рис. 26, можно определить границу X площади А_с из условия:

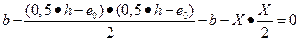, откуда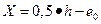

и, следовательно, для прямоугольного сечения получим:

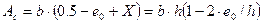(13)