Напряжения и деформации при растяжении-сжатии

Растяжение или сжатие прямого бруса – это вид нагружения, при котором в поперечном сечении бруса возникает только продольная сила. Если продольная сила направлена от сечения, то брус – растянут. В противном случае он будет сжат. Растяжение считается положительной деформацией, а сжатие – отрицательной. Если на различные участки бруса действуют разные по величине и направлению силы, то они будут находиться в различном напряженном состоянии. Напряжения в участках бруса оценивают по эпюрам напряжений.

Эпюра продольной силы в прямом брусе – это график распределения продольной силы вдоль его оси (рис. 4).

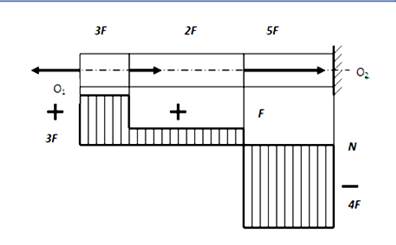
Рис. 4 Эпюра продольных сил в прямом брусе

Ось эпюры параллельна продольной оси бруса. Если на разных участках бруса действуют различные силы, то в пределах каждого участка их величина остается неизменной, а при переходе к следующему участку изменяется: противоположно направленные силы вычитаются, однонаправленные – складываются. Правильность построения эпюры проверяется по наличию скачка сил в месте приложения внешней силы. На эпюре проставляют значения реакции N = F_i – F_i+1 . При построении эпюры сил в закрепленном стержне используют принцип смягчения граничных условий: в точках тела, удаленных от мест приложения нагрузки, модуль внутренних сил мало зависит от способа закрепления.

При построении эпюр напряжений стержень разбивают на участки, в пределах которых силы неизменны по величине, а в пределах каждого участка учитывают изменение площади поперечного сечения. Таким образом, эпюра напряжений в общем не соответствует эпюре приложенных сил (рис. 5).

При этом используют гипотезу плоских сечений: поперечное сечение бруса, плоское и перпендикулярное оси, после деформации остается плоским и перпендикулярным оси.

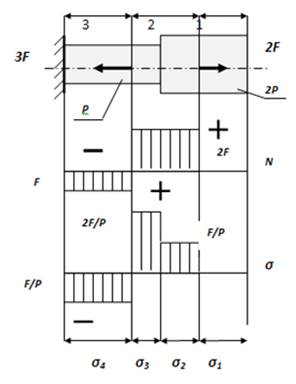
Рис. 5 Эпюры сил и напряжений в прямом ступенчатом брусе

При растяжении и сжатии в сечении действуют только нормальные напряжения, величина которых прямо пропорциональна действующей силе N и обратно пропорциональна площади поперечного сечения Р.

По величине напряжений, действующих в теле, осуществляют расчет на прочность, под которой понимают способность тела сопротивляться разрушению по действием внешних сил.

Используется два метода расчета на прочность: проектный и поверочный. В первом случае определяют:

- предельные размеры детали по площади поперечного сечения Р = N /σ;

- выбирают материал детали по пределу прочности σ = N / Р.

При поверочном расчете проверяют выполнение условия: σ = N / Р < [σ], где [σ] – предел прочности – максимальные напряжения, которые данный материал выдерживает без разрушения.

Закон Гука

До тех пор, пока напряжения в теле не превышают предела пропорциональности, между напряжением и деформацией имеет место линейная зависимость, представляющая собой закон Гука:

σ = Еε, (1)

где Е – модуль продольной упругости (модуль Юнга);

ε – относительная деформация.

Поскольку σ =N / F, а ε = Δl / l, то из выражения (1) следует, что:

Δl = N l / E F (2)

Произведение E F представляет собой жесткость поперечного сечения при растяжении.

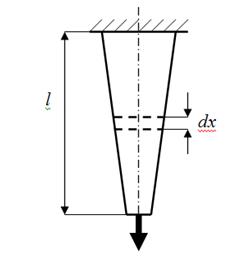
В общем случае стержня переменного сечения (рис. 6) выражение (2) может быть представлено в интегральной форме:

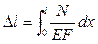P

Рис. 6 Растяжение стержня переменного сечения

Закон Пуассона

Опытным путем установлено, что при простом растяжении-сжатии отношение величины поперечной деформации продольной есть величина постоянная для данного материала. Это отношение, взятое по модулю, представляет собой коэффициент Пуассона:

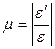где ε’ и ε – поперечная и продольная деформации (соответственно).

Коэффициент Пуассона изменяется в пределах от 0 для пробки до 0,5 для каучука и наряду с модулем Юнга является одной из важнейших механических характеристик материалов.