Дифференциальные зависимости между M,Q и q.

Рассмотрим балку с внешней распределенной нагрузкой интенсивностью 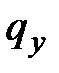, направленной вниз вдоль положительной оси y (рис.7.6 а). Такую нагрузку будем считать положительной. Выделим из нее в произвольном месте элемент длиной 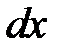(рис 7.6 б). Действие левой отброшенной части на элемент заменим поперечной силой 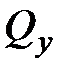и изгибающим моментом 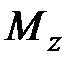, а действие правой отброшенной части -

силой 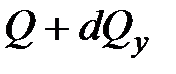и моментом .

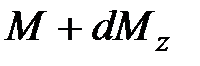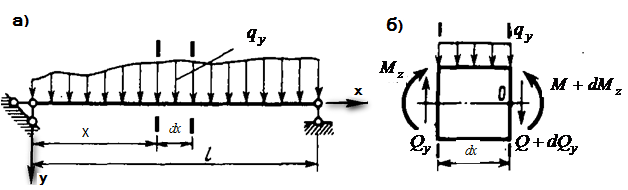
Рис 7.6 К выводу дифференциальных зависимостей

Здесь 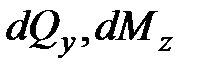- приращение поперечной силы и изгибающего момента на элементе 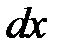. На малом элементе 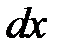интенсивность нагрузки 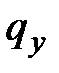можно считать постоянной. Составим уравнения равновесия:

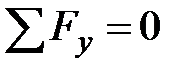
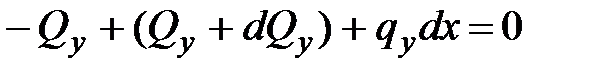
(7.1)

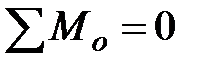
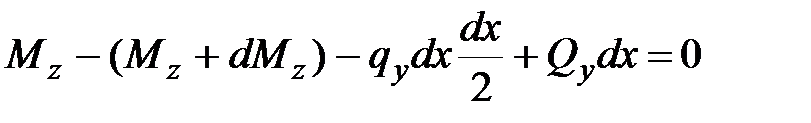
(7.2)

Из уравнения (7.1) получим

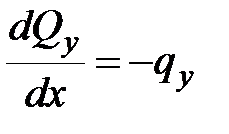
(7.3)

Первая производная от поперечной силы по продольной координате xравна интенсивности распределенной нагрузки, взятой с обратным знаком.

Из уравнения (7.2), пренебрегая слагаемым 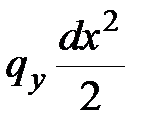как величиной второго порядка малости, получим

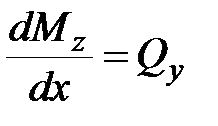
(7.4)

Первая производная от изгибающего момента по продольной координате xравна поперечной силе.

Зависимость (7.3) с учетом (7.4) можно записать в виде

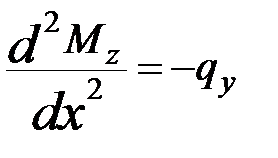
(7.5)

Вторая производная от изгибающего момента по продольной координате xравна интенсивности распределенной нагрузки, взятой с обратным знаком .В дальнейшем индексы у 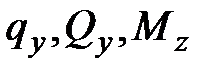будем опускать.