Высокочастотная электропроводность металлов.

Если в металле существует переменное электрическое поле 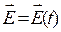, возникновением при этом магнитного поля пренебрегаем, то уравнение движения электрона проводимости «в среднем» приобретает вид

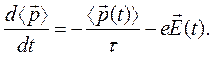(1)

Произвольное поле 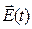можно представить себе как суперпозицию отдельных гармонических колебаний вида 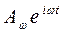, поэтому представляет интерес исследовать решения уравнения (1) при условии

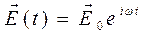, (2)

где 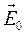- постоянный вектор. Если рассматривать процесс установившихся колебаний

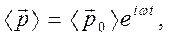(3)

то, подставляя выражение (3) в уравнение (1) с учетом соотношения (2), убеждаемся, что необходимо выполнить условие

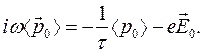(4)

Решением уравнения (4) является выражение

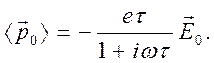(5)

Выражение (5) позволяет записать дифференциальную форму закона Ома в виде

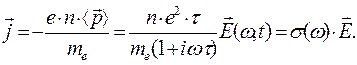(6)

Из уравнения (6) формально следует

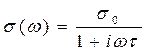, (7)

где 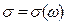- комплексная величина, зависящая не только от свойств вещества (параметры), но и от параметра внешнего воздействия.

Перепишем соотношение (7) в эквивалентной форме:

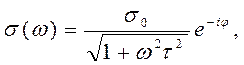(8)

где 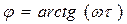. В этом случае соотношение (6) приобретает вид:

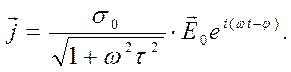(9)

Вспоминая предположение (2), замечаем, что ток отстает по фазе от фазы колебаний напряженности поля на угол 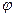, а модуль величины 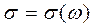оказывается зависящим от частоты 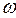колебаний вектора 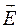. Очевидные следствия из соотношения (8): при 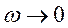величина 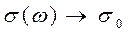, т.е. к своему статическому значению; при 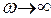величина 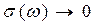, быстропеременное поле 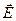«не успевает» разогнать электроны, обладающие свойством инерции.