Электропроводность металлов.
Теория Друде на уровне элементарных молекулярно-кинетических представлений обосновывает закон Ома. Рассмотрим закон Ома для однородного участка цепи в дифференциальной форме:
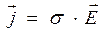 , (1)
, (1)
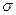 - электропроводность,
- электропроводность, 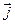 - плотность тока,
- плотность тока, 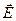 - напряженность электрического поля. Вспомним, что величина
- напряженность электрического поля. Вспомним, что величина 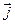 - плотность потока электрического заряда
- плотность потока электрического заряда
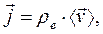
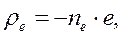 (2)
(2)
где 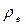 - объёмная плотность электрического заряда,
- объёмная плотность электрического заряда, 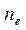 - объёмная концентрация носителей заряда,
- объёмная концентрация носителей заряда, 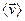 - вектор средней скорости направленного движения носителей заряда, в рассматриваемом случае – электронов. В отсутствие напряженности электрического поля
- вектор средней скорости направленного движения носителей заряда, в рассматриваемом случае – электронов. В отсутствие напряженности электрического поля 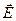 величина
величина 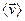 обращается в нуль (хотя хаотическое тепловое движение электронов продолжает иметь место). Для случая
обращается в нуль (хотя хаотическое тепловое движение электронов продолжает иметь место). Для случая 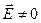 величина
величина 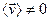 и направлена противоположно полю. Эту скорость можно рассчитать следующим образом. Пусть t – время, прошедшее с момента последнего соударения электрона с рассеивающим центром. Мгновенная скорость
и направлена противоположно полю. Эту скорость можно рассчитать следующим образом. Пусть t – время, прошедшее с момента последнего соударения электрона с рассеивающим центром. Мгновенная скорость 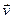 электрона в момент времени t равна:
электрона в момент времени t равна:
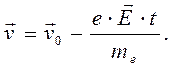 (3)
(3)
Из-за «хаотичности» начальной скорости 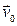 ее вклад в среднюю скорость частицы равен нулю. Линейный характер зависимости скорости от времени (3) приводит к тому, что за описываемый промежуток времени средняя скорость движения оказывается равной скорости для момента времени
ее вклад в среднюю скорость частицы равен нулю. Линейный характер зависимости скорости от времени (3) приводит к тому, что за описываемый промежуток времени средняя скорость движения оказывается равной скорости для момента времени 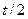 . При осреднении мгновенной скорости направленного движения электронов полагают, что характерное время движения между соударениями (с постоянной скоростью)
. При осреднении мгновенной скорости направленного движения электронов полагают, что характерное время движения между соударениями (с постоянной скоростью)
cовпадает со временем релаксации 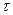 :
:
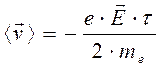 . (4)
. (4)
Учитывая зависимости (1), (2) и (4), получим выражение для проводимости 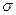 :
:
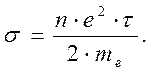 (5)
(5)
Заметим, что по Ланжевену из соотношения (4) следует выражение для «подвижности» электронов проводимости в металле:
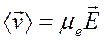
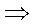
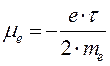 . (6)
. (6)
Если по экспериментальным данным для удельного электрического сопротивления среды 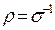 оценить величину
оценить величину 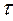 для металлов, она оказывается величиной порядка 10-14 – 10-15 с. Оценить длину свободного пробега можно соотношением
для металлов, она оказывается величиной порядка 10-14 – 10-15 с. Оценить длину свободного пробега можно соотношением
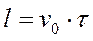 , (7)
, (7)
а значение 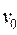 можно получить из классического закона распределения энергии молекул по степеням свободы
можно получить из классического закона распределения энергии молекул по степеням свободы
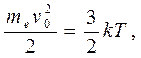 (8)
(8)
где k – постоянная Больцмана, Т – абсолютная температура металла. Из зависимости (8) при комнатной температуре получаем 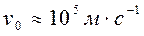 , а
, а 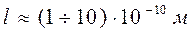 .
.
Значение величины l удивительно совпало с возможными значениями межатомных расстояний в твёрдом теле... Вроде бы теория Друде «правильно» описала механизм рассеяния электронов... На самом деле картина рассеяния имеет более сложную природу. И эксперимент не свидетельствует в пользу теории Друде: при достаточно низких температурах на тщательно приготовленных образцах можно получить 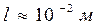 , т.е. 108 (сто миллионов!) межатомных расстояний.
, т.е. 108 (сто миллионов!) межатомных расстояний.
Итак, если бы мы знали величину параметра 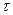 , то зависимость (5) решала бы проблему расчета величины
, то зависимость (5) решала бы проблему расчета величины 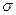 . Вместе с тем, результаты теории Друде, не содержащие время релаксации
. Вместе с тем, результаты теории Друде, не содержащие время релаксации 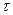 , оказываются количественно верными.
, оказываются количественно верными.
Теория Друде объясняет физическую природу закона Джоуля-Ленца следующим образом. При каждом «соударении» с рассеивающим центром электрон полностью передает этому центру энергию
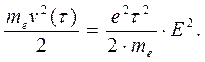 (9)
(9)
За единицу времени происходит 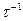 таких соударений. А если учесть, что в единице объема содержится n электронов, то получим, в единице объема кристаллической решетки металла за единицу времени выделяется энергия, равная
таких соударений. А если учесть, что в единице объема содержится n электронов, то получим, в единице объема кристаллической решетки металла за единицу времени выделяется энергия, равная
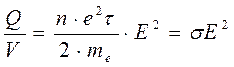 . (10)
. (10)
Заметим, что величина объёмной плотности тока определялась величиной средней скорости направленного движения электронов между соударениями, величина удельного тепловыделения – максимальной скоростью направленного движения электронов между соударениями.
Соотношение (10) обосновывает дифференциальную форму закона Джоуля-Ленца в рамках молекулярно-кинетических представлений.
Теория Друде впервые объяснила природу эмпирического закона Видемана и Франца, установленного ещё в 1853 г., в котором утверждалось, что отношение коэффициента теплопроводности к коэффициенту электропроводности (т.е. электрической проводимости) для большинства металлов является величиной, прямо пропорциональной абсолютной температуре, причем коэффициент пропорциональности приблизительно одинаков. Из элементарной молекулярно-кинетической теории газов известно выражение для коэффициента теплопроводности
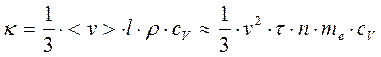 , (11)
, (11)
где 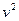 - средний квадрат скорости электрона,
- средний квадрат скорости электрона, 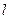 - длина свободного пробега,
- длина свободного пробега, 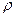 - объёмная плотность,
- объёмная плотность, 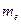 - масса электрона,
- масса электрона, 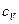 - теплоёмкость при постоянном объёме в расчёте на единицу массы. Разделим приведенное выражение на коэффициент электропроводности среды (5):
- теплоёмкость при постоянном объёме в расчёте на единицу массы. Разделим приведенное выражение на коэффициент электропроводности среды (5):
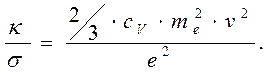 (12)
(12)
Заметим, что полученное соотношение не зависит от времени релаксации 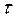 и в силу этого может оказаться достаточно эффективным. В рамках классических представлений
и в силу этого может оказаться достаточно эффективным. В рамках классических представлений 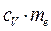 - это теплоёмкость электронного газа при постоянном объёме в пересчёте на один электрон,
- это теплоёмкость электронного газа при постоянном объёме в пересчёте на один электрон, 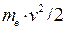 - средняя энергия теплового движения электрона. Это даёт возможность записать следующие соотношения:
- средняя энергия теплового движения электрона. Это даёт возможность записать следующие соотношения:
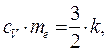
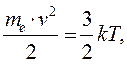
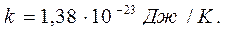 (13)
(13)
В окончательной форме получаем соотношение:
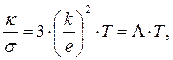 (14)
(14)
где 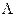 - число Лоренца. По приведенной формуле число Лоренца получается примерно в два раза меньше, чем следует из совокупности экспериментальных данных. Сам Друде при расчете величины электропроводности среды ошибся в два раза, поэтому рассчитанное им значение числа Лоренца «совпало» с экспериментом на удивление точно. Триумф теории Друде способствовал всестороннему её анализу и расширению сферы её применения. В самом начале XX века А. Зоммерфельдом (1868-1951) была предпринята попытка разработать электронную теорию металлов с последовательным использованием максвелловского распределения электронов по скоростям. Вскоре выяснилось, что электронная теплоемкость металлов приблизительно в сто раз меньше, чем принятая в теории Друде, а средний квадрат скорости электронов приблизительно в сто раз больше. Этим объясняется удивительное совпадение отдельных результатов теории Друде с результатами экспериментальных исследований. Но в целом классическая статистическая теория оказалась неприменимой к описанию электронного газа в металлах. Электроны в металлах обладают специфическими квантовыми свойствами и подчиняются квантовой статистике Ферми-Дирака.
- число Лоренца. По приведенной формуле число Лоренца получается примерно в два раза меньше, чем следует из совокупности экспериментальных данных. Сам Друде при расчете величины электропроводности среды ошибся в два раза, поэтому рассчитанное им значение числа Лоренца «совпало» с экспериментом на удивление точно. Триумф теории Друде способствовал всестороннему её анализу и расширению сферы её применения. В самом начале XX века А. Зоммерфельдом (1868-1951) была предпринята попытка разработать электронную теорию металлов с последовательным использованием максвелловского распределения электронов по скоростям. Вскоре выяснилось, что электронная теплоемкость металлов приблизительно в сто раз меньше, чем принятая в теории Друде, а средний квадрат скорости электронов приблизительно в сто раз больше. Этим объясняется удивительное совпадение отдельных результатов теории Друде с результатами экспериментальных исследований. Но в целом классическая статистическая теория оказалась неприменимой к описанию электронного газа в металлах. Электроны в металлах обладают специфическими квантовыми свойствами и подчиняются квантовой статистике Ферми-Дирака.
8.4.2. Эффект Холла.
Для наших целей наибольший интерес представляют два случая: расчет электропроводности при наличии пространственно-однородного постоянного магнитного поля (эффект Холла) и при наличии пространственного однородного, но переменного во времени электрического поля.
Перед началом рассмотрения этих случаев обсудим уравнение второго закона Ньютона для среднего значения импульса электрона
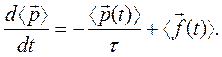 (1)
(1)
Смысл уравнения (1) состоит в следующем. Величина 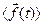 - осредненная внешняя сила, действующая на электрон. Величина
- осредненная внешняя сила, действующая на электрон. Величина 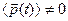 является количественной мерой отклонения системы от состояния равновесия. В равновесных условиях величина
является количественной мерой отклонения системы от состояния равновесия. В равновесных условиях величина 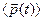 равна нулю (это основное условие хаотичности движения электронов). Каждая устойчивая система стремится к состоянию равновесия со скоростью, пропорциональной (в нулевом приближении) величине этого отклонения. Таким образом, уравнение (1) представляет собой типичное уравнение релаксационного процесса.
равна нулю (это основное условие хаотичности движения электронов). Каждая устойчивая система стремится к состоянию равновесия со скоростью, пропорциональной (в нулевом приближении) величине этого отклонения. Таким образом, уравнение (1) представляет собой типичное уравнение релаксационного процесса.
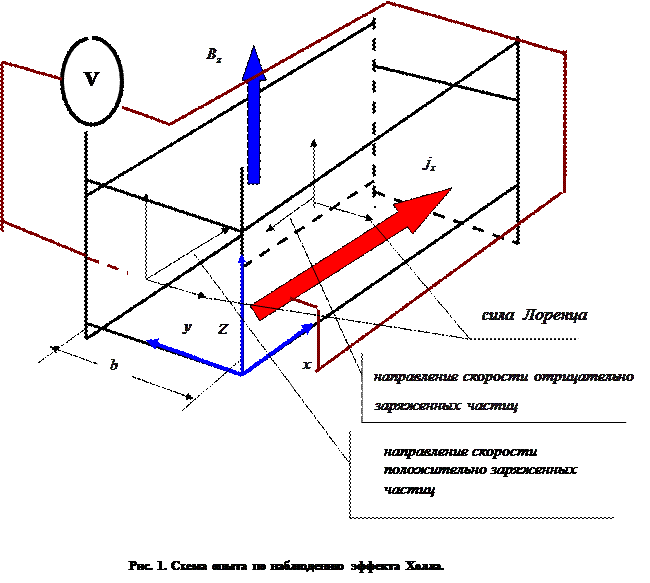
Пусть по проводнику вдоль оси х (рис.1) течет электрический ток с плотностью jx под действием напряжённости электрического поля 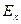 (на рисунке не показана) при наличии поперечного магнитного поля
(на рисунке не показана) при наличии поперечного магнитного поля 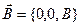 , т.е. направленного вдоль оси z. Под влиянием силы Лоренца, действующей на каждую заряженную частицу, возникают компоненты напряженности электрического поля Ey и плотности тока
, т.е. направленного вдоль оси z. Под влиянием силы Лоренца, действующей на каждую заряженную частицу, возникают компоненты напряженности электрического поля Ey и плотности тока 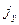 . Уравнение (1) для движения электронов в металле принимает вид
. Уравнение (1) для движения электронов в металле принимает вид
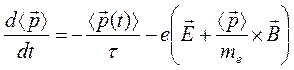 . (2)
. (2)
Для установившегося режима средний импульс электрона не зависит от времени, поэтому:
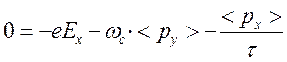 , (3)
, (3)
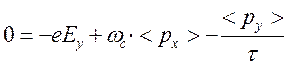 , (4)
, (4)
где
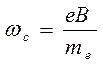 . (5)
. (5)
Умножая уравнения (3) и (4) на выражение 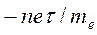 и учитывая определение плотности тока
и учитывая определение плотности тока
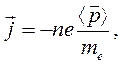 (6)
(6)
получаем
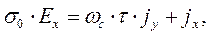 (7)
(7)
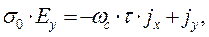 (8)
(8)
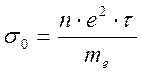 . (9)
. (9)
Поле Холла Ey определяется условием jy=0. Из уравнения (8) при этом следует:
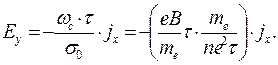 (10)
(10)
Следовательно, для коэффициента Холла получаем
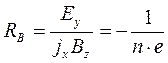 . (11)
. (11)
Результат (11) примечателен тем, что коэффициент Холла не зависит ни от каких параметров металла, кроме объемной плотности носителей заряда. Для многих металлов соотношение (11) имеет экспериментальное подтверждение, хотя в отдельных случаях расхождение довольно значительное. Для полупроводников по знаку постоянной Холла судят о природе основных носителей электрического заряда в полупроводнике и относят его к р-типу (носитель - положительные «дырки») или n-типу (носитель - электроны с отрицательным электрическим зарядом).
Дата добавления: 2017-09-01; просмотров: 1620;











