Напряжённость электростатического поля, образованного электрическим зарядом, распределённым сферически симметрично по объёму шара.

С помощью теоремы Гаусса можно рассчитать напряжённость электростатического поля, образованного электрическим зарядом, распределённым сферически симметрично по объёму шара радиуса а. Начало сферической системы координат совместим с центром заряженного шара. В рассматриваемом случае объёмная плотность электрического заряда является функцией радиальной координаты и не зависит от угловых переменных. В этих условиях следует ожидать, что единственная отличная от нуля радиальная компонента напряжённости электростатического поля будет иметь постоянное значение на произвольной замкнутой сферической поверхности, центр которой совпадает с началом координат.

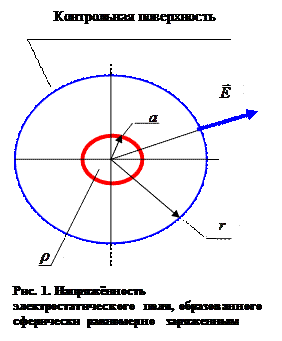Эта компонента одновременно является нормальной составляющей вектора напряжённости к элементам контрольной поверхности (рис.1). Интегральная форма теоремы Гаусса в рассматриваемом случае приводит к зависимости:

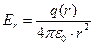. (1)

Величина электрического заряда внутри контрольной поверхности 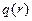вычисляется по-разному, для случая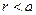

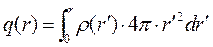, (2)

для случая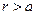

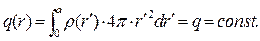(3)

Поскольку 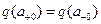, то радиальная компонента электростатического поля непрерывна при :

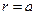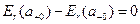. (4)

В частном случае, когда электрический заряд равномерно распределен по объёму шара ( 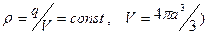, величина заряда внутри контрольной поверхности (r<a) определяется выражением

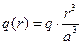, (5)

что позволяет выписать зависимость напряжённости электростатического поля внутри шара с равномерным распределением электрического заряда:

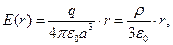
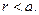(6)

Для точек наблюдения с радиальными координатами 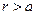зависимость величины напряжённости электростатического поля определяется соотношениями (1) и (3).

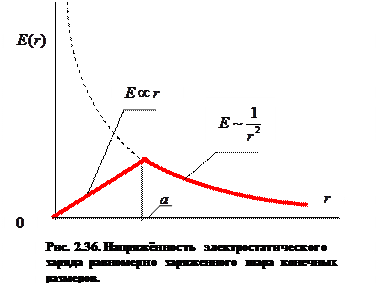
Зависимость напряжённости электростатического поля равномерно по объёму заряженного шара от радиальной координаты точки наблюдения показана на рис.2.

Рассмотрим дифференциальную форму теоремы Гаусса применительно к описанному распределению электрических зарядов в пространстве. В условиях сферической симметрии имеем:

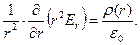(7)

Для напряжённости электростатического поля внутри заряженного шара получаем общее решение дифференциального уравнения (7): 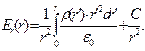(8)

Поскольку распределение электрического заряда сферически симметрично, легко показать, что напряжённость электростатического поля в центре шара должна обращаться в нуль, поэтому постоянную интегрирования С следует положить равной нулю:

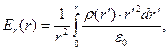
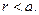(9)

Общее решение уравнения (7) для области вне шара, где 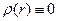, имеет вид:

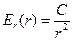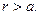, (10)

Постоянную интегрирования С в этой зависимости можно определить либо из условия непрерывности нормальной к поверхности шара радиальной компоненты вектора напряжённости электростатического поля, либо вычисляя поток вектора через поверхность шара и используя интегральную форму теоремы Гаусса:

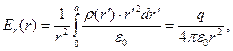
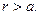(11)

Приравнивая выражения (9) и (10) при 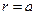, получаем значение постоянной интегрирования С в соотношении (10): .

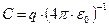Электростатическое поле сферически симметрично заряженного шара вне шара совпадает с полем одиночного сосредоточенного заряда, расположенного в центре шара, величина сосредоточенного заряда равна заряду шара.

2.3.6.4. Напряжённость электростатического поля, образованного прямой бесконечной нитью с равномерным распределением электрического заряда.

В рассматриваемом случае (рис.1) линейная плотность электрического заряда прямолинейной нити удовлетворяет условию 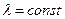. Суммарный электрический заряд нити при этом формально является бесконечно большой величиной, в реальности подобная абстракция вполне уместна при расчёте напряженности электростатического поля в точках пространства, расстояния от которых до концов прямолинейной нити значительно больше, чем кратчайшее расстояние до заряженной нити.

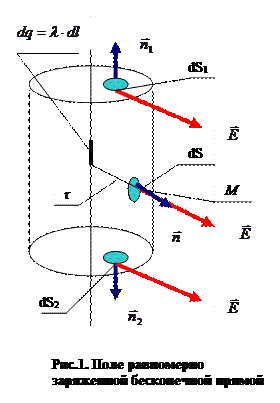Рассмотрим интегральную форму теоремы Гаусса. В качестве контрольной поверхности выберем круговую цилиндрическую поверхность, проходящую через точку наблюдения М, ось этой поверхности совпадает с прямолинейной нитью. Замыкание контрольной поверхности осуществим плоскостями, перпендикулярными оси симметрии, расположенными выше и ниже точки наблюдения М, так, чтобы высота построенного цилиндра оказалась равной l . Для произвольной точки пространства вектор напряжённости электростатического поля в условиях осевой симметрии пространственного расположения электрического заряда будет иметь только радиальную составляющую. Действительно, для каждого произвольного отрезка нити с зарядом 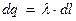на бесконечной прямой найдётся точно такой же отрезок, симметрично расположенный относительно точки наблюдения М, что обратит в нуль осевую составляющую вектора напряженности (рис.2). В этих условиях потоки вектора напряженности через торцевые поверхности S₁ и S₂ равны нулю, а поток через боковую поверхность цилиндра равен 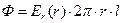. Электрический заряд внутри контрольной поверхности равен 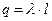. Используя интегральную форму теоремы Гаусса, получаем:

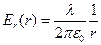. (1)

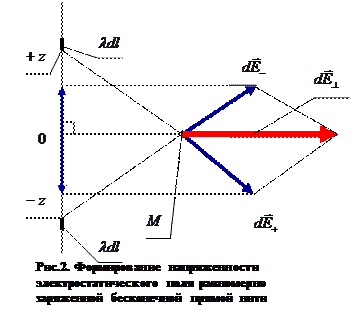Этот результат можно получить и применением дифференциальной формы теоремы Гаусса. В условиях осевой симметрии пространственного расположения электрического заряда напряжённость поля не имеет осевой составляющей, не имеет составляющей вдоль угловой координаты, отлична от нуля одна радиальная составляющая вектора, которая зависит только от радиальной координаты точки наблюдения. Дифференциальное уравнение теоремы Гаусса (цилиндрическая система координат) принимает вид

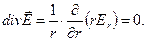(2)

Решением этого уравнения является выражение 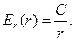(3)

Постоянную интегрирования С приходится определять с использованием интегральной формы теоремы Гаусса.

2.3.6.5. Напряжённость электростатического поля, образованного бесконечным круговым цилиндром с равномерным распределением заряда по поверхности.

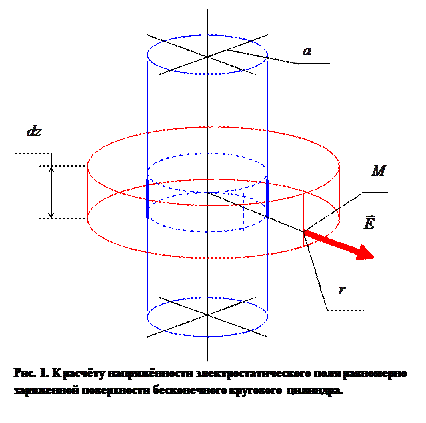Рассмотрим круговой цилиндр с радиусом поперечного сечения 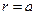и высотой 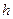, на боковой поверхности которого равномерно распределён электрический заряд с поверхностной плотностью 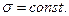Условимся рассматривать такие точки пространства М, которые настолько удалены от торцевых поверхностей заряженного цилиндра, что последний условно можно считать бесконечно длинным в осевом направлении. При использовании интегральной формы теоремы Гаусса для расчёта напряжённости электростатического поля в точке наблюдения М в качестве контрольной поверхности выбираем поверхность соосного с исходным цилиндра высотой dz, боковая поверхность которого содержит точку наблюдения М (рис. 1). В условиях осевой симметрии распределения электрического заряда и симметрии распределения заряда вдоль осевой линии цилиндра напряжённость электростатического поля может иметь только радиальную компоненту, величина которой меняется только в зависимости от радиальной координаты соответствующей цилиндрической системы координат. Поскольку радиальное направление является нормальным к боковой поверхности контрольного объёма и касательным направлением к его торцевым поверхностям, поток вектора напряженности электростатического поля через контрольную поверхность равен 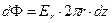(r>a), а величина электрического заряда в контрольном объёме равна 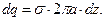В этом случае из интегральной формы теоремы Гаусса следует

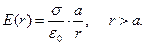(1)

Для точек наблюдения М, расположенных внутри равномерно заряженной цилиндрической поверхности, можно повторить приведенные выше рассуждения, с той лишь разницей, что в рассматриваемом случае величина электрического заряда внутри контрольной поверхности тождественно равна нулю, а вместе с ней равна нулю и напряжённость электростатического поля.

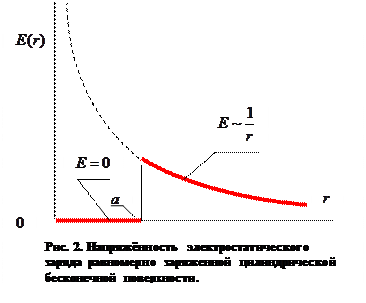
Графическая иллюстрация

полученных результатов приведена на рис. 2. Характер этой зависимости качественно похож на зависимость напряжённости электростатического поля равномерно заряженной сферы, рассмотренной выше. Легко видеть, что скачок нормальной компоненты напряжённости при пересечении заряженной поверхности 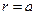равен поверхностной плотности электрического заряда 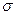, делённой на электрическую постоянную .

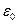При использовании дифференциальной формы теоремы Гаусса в цилиндрической системе координат для рассматриваемого случая 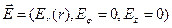приходится решать дифференциальное уравнение

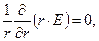
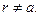(2)

Общее решение этого уравнения имеет вид

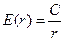. (3)

Приведенная форма решения справедлива и для 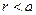, и для 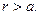Из физических соображений ясно, что на оси симметрии распределения электрического заряда напряжённость электростатического поля должна обратиться в нуль, значит для области внутри заряженной цилиндрической поверхности постоянная интегрирования равна нулю. Для наружной области величину С можно определить, зная величину напряженности во внутренней области и величину скачка нормальной составляющей при переходе через заряженную поверхность:

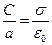. (4)

В результате имеем зависимость

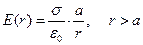, (5)

полностью совпадающую с зависимостью, полученной выше.

2.3.6.6. Напряжённость электростатического поля бесконечного кругового цилиндра с равномерным распределением заряда по азимутальной и осевой координатам и произвольным распределением по радиальной координате.

Для рассматриваемого случая (объёмная плотность электрического заряда удовлетворяет условию 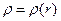) можно воспользоваться рассуждениями анализа электростатического поля бесконечно цилиндра с радиусом поперечного сечения а с равномерной по поверхности плотностью электрического заряда, только учесть, что в элементарном объёме содержится заряд 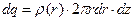, а в выделенном контрольном объёме содержится заряд

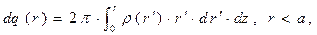(1)

или

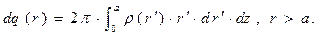(2)

Интегральная форма теоремы Гаусса позволяет получить зависимость напряжённости электростатического поля от радиальной координаты:

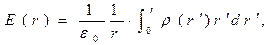
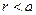(3)

или

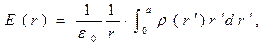
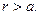(4)

В случае равномерного распределения электрического заряда по объёму заряженного цилиндра имеем соответственно:

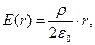
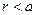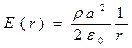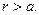или , (5)

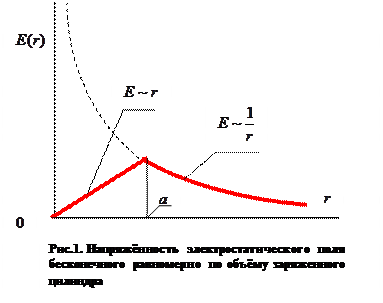Графическая иллюстрация полученных результатов показана на рис 1. Качественно картина распределения напряжённости по радиальной координате похожа на аналогичную картину поля равномерно по объёму заряженного шара, изменился только характер зависимости вне заряженной области: напряжённость электростатического поля вне шара была пропорциональна r^-2, а для цилиндра стала пропорциональна r^-1.

Полезно обратить внимание на то, что напряженность электростатического поля при 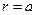в отсутствие поверхностной плотности электрического заряда на боковой поверхности цилиндра остаётся непрерывной величиной.

Рассмотрим дифференциальную форму теоремы Гаусса применительно к расчёту напряжённости электростатического поля бесконечного цилиндра с объёмной плотностью заряда 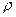, зависящей только от радиальной координаты. Повторяя рассуждения, проведённые выше при рассмотрении интегральной формы теоремы Гаусса, приходим к заключению, что единственной отличной от нуля составляющей вектора напряженности 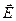является радиальная составляющая, которая в свою очередь зависит от радиальной координаты. Запишем дифференциальное уравнение, которое получается из дифференциальной формулировки теоремы Гаусса в рассматриваемом случае:

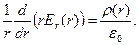(6)

Для случая 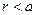решение этого уравнения имеет вид:

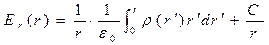. (7)

Из физических соображений очевидно, что напряжённость электростатического поля на оси заряженного цилиндра не может обратиться в бесконечность, поэтому постоянную интегрирования следует положить равной нулю. Для случая 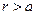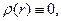поэтому решение рассматриваемого уравнения будет иметь вид:

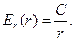(8)

Постоянную интегрирования С при этом проще всего определить из условия непрерывности радиальной компоненты напряжённости электростатического поля при переходе через боковую поверхность заряженного цилиндра в отсутствие поверхностной плотности электрического заряда на этой поверхности:

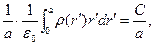(9)

в итоге получаем зависимость

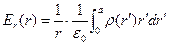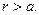, (10)

Если объёмная плотность электрического заряда внутри цилиндра постоянна, имеют место соотношения:

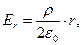
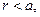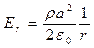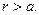или , (11)

Естественно, что эти результаты тождественны результатам решения, основанного на интегральной форме теоремы Гаусса.

2.3.6.7. Напряженность электростатического поля бесконечной плоскости с равномерным распределением заряда по поверхности.

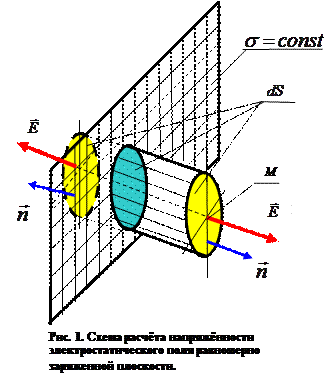Рассмотрим достаточно большой участок плоскости произвольной формы в плане с поверхностной плотностью электрического заряда 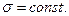Пусть произвольная точка пространства М, в которой необходимо рассчитать напряжённость электростатического поля, находится недалеко от заряженной плоскости, но далеко от её краёв. В этом случае уместно принять, что заряженная плоскость имеет неограниченные размеры. Пусть ос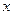и и 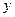декартовой системы координат расположены в плоскости, а ось 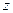ориентирована перпендикулярно плоскости и проходит через точку наблюдения М. Из условий симметрии распределения электрического заряда относительно начала координат следует, что вектор напряжённости электростатического поля должен быть направлен по нормали к плоскости. Контрольную поверхность в интегральной формулировке теоремы Гаусса удобно выбрать в форме цилиндра с произвольным поперечным сечением, одна из торцевых его поверхностей пусть проходит через точку наблюдения М, а вторая является зеркальным отражением первой относительно заряженной плоскости. Поток вектора напряжённости 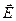через боковую поверхность равен нулю: вектор 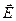параллелен каждому элементу боковой поверхности контрольного цилиндра. Равные между собой потоки вектора 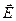через торцевые плоские поверхности цилиндра равны 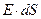, где 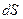- площадь торцевой плоской поверхности цилиндра. Суммарный поток вектора 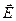через замкнутую контрольную поверхность составляет 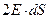, а суммарный электрический заряд в контрольном объёме, находящийся на элементе поверхности 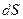заряженной плоскости равен 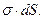По условию теоремы Гаусса получаем:

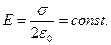(1)

В дифференциальном подходе для нормальной к заряженной плоскости компоненты вектора 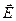имеем уравнение

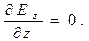(2)

Общее решение его – произвольная постоянная. Определить значение произвольной постоянной в рассматриваемом случае можно только с привлечением интегральной формулировки теоремы Гаусса.

В заключение раздела заметим, что разобранные примеры использования интегральной и дифференциальной форм теоремы Гаусса для напряженности электростатического поля могут служить основой для рассмотрения комбинированных случаев на основе принципа суперпозиции.