Интегральная форма теоремы Гаусса для вектора напряженности электростатического поля в вакууме.

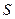Поток вектора напряженности электростатического поля через замкнутую поверхность обладает специфическим свойством: его величина пропорциональна электрическому заряду, расположенному внутри этой поверхности. Это утверждение составляет физический смысл теоремы Гаусса. Теорема Гаусса для вектора напряженности электростатического поля 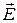в вакууме является следствием закона Кулона. Теорема Гаусса имеет большое значение в теории электромагнетизма. Доказательство ее справедливости включает три этапа.

Первый этап. Допустим, что в начале координат помещен точечный электрический заряд 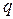. Напряженность электростатического поля, созданного этим зарядом, описывается соотношением:

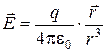, (1)

где 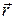- радиус-вектор точки наблюдения, 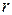- его модуль. Окружим заряд 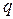сферой радиуса 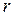, центр которой совпадает с началом координат. Известно, что внешняя нормаль 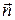к элементу поверхности 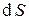сферы направлена по радиусу:

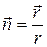. (2)

Действительно, поверхность сферы радиуса 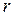с центром в начале координат описывается уравнением

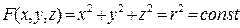. (3)

В соответствии с определением нормали к поверхности вычисляем

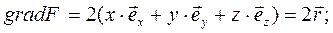
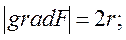
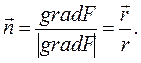(4)

Поток вектора 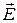через поверхность сферы равен:

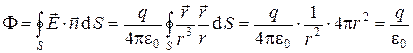. (5)

Запомним этот результат.

Второй этап. Пусть поверхность 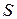является произвольной достаточно гладкой замкнутой поверхностью, причем начало координат - место расположения заряда 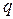- лежит внутри поверхности 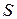. В этом случае прямое вычисление потока вектора 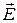через замкнутую поверхность 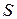приводит к результату

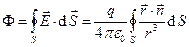. (6)

Заметим, что имеют место соотношения:

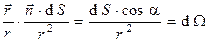, (7)

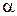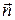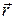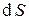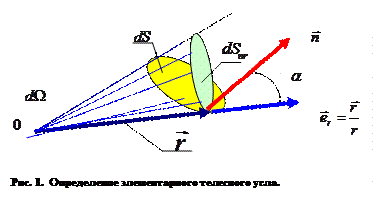
где - угол между внешней нормалью и радиус-вектором точки, в окрестности которой расположен элемент поверхности , 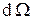- элемент телесного угла, под которым виден элемент поверхности 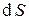из начала координат (Рис.1). С учётом соотношений (7) выражение (6) приобретает вид:

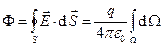. (8)

При записи выражения (8) следует иметь в виду, что для строго выпуклой замкнутой поверхности 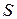величина элементарного телесного угла положительна 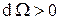и суммарное значение интеграла в выражении (8) равно

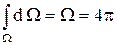. (9)

Если поверхность 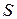не является строго выпуклой, то для части поверхности 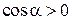, а для части поверхности 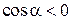, в этом случае величина 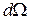является алгебраической величиной, но соотношение (8) остается справедливым.

Для случая, когда начало координат (т.е. точка расположения заряда 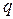) лежит вне замкнутой поверхности, суммарное значение 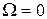, поскольку видимая часть поверхности 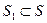и невидимая из начала координат часть поверхности 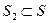, 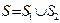приводят к одному и тому же абсолютному значению телесного угла, но противоположных знаков.

Третий этап. Реальное электростатическое поле обусловлено совокупностью «точечных» зарядов (принцип суперпозиции), для каждого из которых соотношение

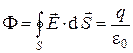
(10)

доказано для произвольной замкнутой поверхности 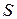. Но тем самым доказана справедливость теоремы Гаусса для произвольного электростатического поля:

поток вектора напряженности электростатического поля через произвольную замкнутую поверхность 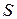равен суммарному электрическому заряду, находящемуся внутри объёма, ограниченного поверхностью 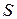, деленному на величину электрической постоянной .

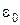Заметим, что соотношение (10) справедливо для системы единиц СИ. То обстоятельство, что замкнутая поверхность 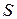в формулировке теоремы Гаусса может быть произвольной, позволяет выбрать ее форму при решении конкретной задачи удобным для исследователя способом.

Использование теоремы Гаусса в интегральной форме (10) в отдельных случаях, отличающихся высокой степенью симметрии расположения электрических зарядов в пространстве, позволяет эффективно рассчитывать характеристики электростатического поля. В общем случае теорема Гаусса в форме (10) может служить для получения оценок характерных величин электростатического поля.