Расчет оптических параметров и параметров передачи ОВ
Рассмотрим ряд практических примеров определения параметров, определяющих условия передачи света по различным типам ОВ таких как:
• диаметр сердцевины (dс = 2а) одномодового ОВ, обеспечивающей при заданных величинах различия ПП сердцевины и оболочки (Δ) одномодовый режим передачи;
• рабочую нормированную частоту (v), при которой при заданных допусках на величины а, Δ в ступенчатом ООВ будет иметь место одномодовый режим передачи;
• эффективный диаметр поля моды («диаметр модового пятна») и зависимость напряженности поля моды НЕ11 от радиуса в поперечном сечении ООВ;
• длину волны отсечки («критическая длина волны») волн более высокого порядка, чем НЕ11 для ООВ;
• числовую апертуру для многомодового ОВ;
• величину Δ для стандартизованных многомодовых ОВ, применяющихся в ОК связи, и число мод при различных рабочих длинах волн;
• нижний предел коэффициента затухания в ОВ;
• ориентировочную длину регенерационного участка;
• уширение импульса в МОВ со ступенчатым и градиентным ППП и в ООВ;
• полосы пропускания ОВ;
• дополнительные потери от изгибов ОВ;
• ориентировочные величины групповой скорости и волновых сопротивлений ОВ.
Расчет диаметра сердцевины ООВ. Задачей расчета является выбор диаметра сердцевины ООВ, обеспечивающего при заданных величинах различия ПП сердцевины и оболочки (Δ) и длине волны (λ) одномодовый режим передачи.
Исходные данные: ОВ со ступенчатым, градиентным или треугольным ППП диапазон Δ=0,001 — 0,005; используемые длины волн λ =1,3; 1,55 мкм.
Решение такой задачи сводится к использованию выражений (2.68) и (2.12) и выбору значения п1 или п2.
Задавшись типом ОВ, у которого сердцевина или оболочка выполнены из чистого кварца, рассчитывают соответственно п1 или п2 при заданной λ по формуле Селмейера для кварцевого стекла (3.1).
Вычислив п1 (или п2), по заданной величине Δ можно определить п2 (или п1).
Задавшись величиной нормированной частоты v, из (2.68) можно вычислить искомую величину dс. Тогда
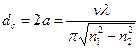 . (4.11)
. (4.11)
Параметр v целесообразно выбирать в пределах 2,0 — 2,3 для получения одномодового режима передачи, т.к. при v0 = 2,405 уже появляется, кроме моды НЕ11 (LР01), следующая мода LР11(табл. 2.3).
Если число v будет выбрано очень близко к v0 = 2,405, то при отклонениях (даже в пределах допусков) от выбранных величин а, Δ, λ ОВ может выйти из одномодового режима передачи (т.е. v может быть равно или меньше 2,405). Если выбрать 2,0, то этому случаю будут соответствовать ОВ с очень малыми значениями а или 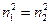 , как следует из (2.68). Это приводит к трудностям в использовании таких ОВ, так как при малых а имеются трудности с вводом энергии и соединением ОВ, а при малой Л наблюдается увеличение потерь на микроизгибах из-за слабой направляемости ОВ.
, как следует из (2.68). Это приводит к трудностям в использовании таких ОВ, так как при малых а имеются трудности с вводом энергии и соединением ОВ, а при малой Л наблюдается увеличение потерь на микроизгибах из-за слабой направляемости ОВ.
Формула (4.11) справедлива для ОВ со ступенчатым ППП. Диаметр сердцевины для ООВ с градиентным ППП (dc') или треугольным ППП (dc ") можно определить при известном значении dc из выражений, пользуясь нижеприведенными соотношениями.
Известно, что функция изменения ПП от радиуса r ОВ с градиентным ППП имеет вид:
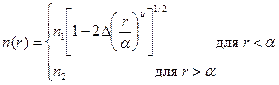
 (4.12)
(4.12)
где и — коэффициент, определяющий ППП, который может принимать любые значения от 1 до ∞(разд. 2.2).
Согласно [2] соотношение между нормированными частотами отсечки для ОВ с разными ППП:
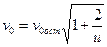 , (4.13)
, (4.13)
где v0ост — нормированная частота отсечки для ОВ со ступенчатым ППП.
Из выражения (4.13) вытекает соотношение, связывающее диаметры сердцевины ОВ с разными ППП, обеспечивающими одномодовый режим передачи:
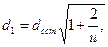 (4.14)
(4.14)
где dсст — диаметр сердцевины ОВ со ступенчатым ППП, определяемый из (4.11).
Как известно, в ОВ со ступенчатым ППП u=∞, с параболическим ППП — и=2, а с треугольным ППП — и=1. Тогда исходя из (4.14) видно, что для ООВ с градиентным и треугольным ППП диаметры сердцевины можно определить из соотношений:
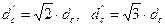 . (4.15)
. (4.15)
Расчет нормированной частоты при одномодовом режиме передачи. Задачей расчета является определение рабочей величины v, при которой сохраняется одномодовый режим работы ступенчатого ООВ при наличии колебания размеров а и Δ в рамках заданных допусков.
Допустим величины Δ и а и их отклонения имеют значения:
• Δ=0,002 — 0,003;
• радиус сердцевины а=6 –10 мкм;
• оносительные отклонения Δ -величины δΔ = ± 5; 10; 15 %;
• относительное отклонение радиуса сердцевины δа= ± 15; 10; 15 %.
Для решения задачи следует определить изменения Δ v, вызванные колебаниями а и Δ в пределах допусков. В этом случае рабочей нормированной частотой (vр) является величина, определяемая из соотношения:
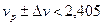 , (4.16)
, (4.16)
которая обеспечит работу ОВ в одномодовом режиме v < 2,405.
Так как по (2.68) величина v пропорциональна а и Δ1/2, то для относительных изменений величины v, а и Δ имеем соотношение:
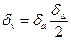 . (4.17)
. (4.17)
Задавшись величинами δа и δΔ определим по (4.17) δv= Δv/v, а затем по (4.16) величину vp. Задаваясь различными значениями δа и δΔ , можно аналогичным образом получить диапазон возможных рабочих значений vp.
Расчет эффективного диаметра поля моды и зависимости E(r) поля моды НЕ11. Целью расчета является определение области сердцевины ООВ, в которой сосредоточено поле волны НЕ11. Эта область определяется величиной dМП, которая носит название диаметра модового поля или эффективного диаметра поля моды.
Исходными данными являются величины vp и dс ,определенные выше.
Радиус поля моды W0 в микрометрах определяется при известных значениях v и a=dс/2 из следующих соотношений (2.72). Искомое значение диаметра поля моды будет dМП =аW0.
Распределение поля в поперечном сечении ОВ E(r) или H(r) можно точно вычислить с помощью решения уравнений (2.38) или (2.39), но для приближенного решения можно воспользоваться аппроксимацией поля моды НЕ11 функцией вида [4]:
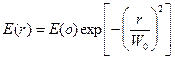 , (4.18)
, (4.18)
где Е(о) — напряженность поля при r=0, зависящая от абсолютной величины мощности оптического сигнала, введенного в ОВ.
Выраженная в относительных величинах зависимость (4.18) имеет вид рис. 4.2.
Значение W0 определенное из рис. 4.2, соответствует уменьшению напряженности Е=2,713  раз по сравнению с Е в центре ОВ (r=0).
раз по сравнению с Е в центре ОВ (r=0).
Для построения зависимости Е(r)/Е(о) следует, задаваясь значениями радиуса r в пределах 0-3а по (4.18), определить искомую величину.
Обычно W0 незначительно превышает радиус сердцевины а, т.е. поле незначительно проникает в оболочку ОВ.
 Расчет длины волны отсечки. Задачей расчета является определение длины волны отсечки мод более высокого порядка, чем волна НЕ11, соответствующая режиму передачи ООВ, при заданных величинах dс, Δ и λ.
Расчет длины волны отсечки. Задачей расчета является определение длины волны отсечки мод более высокого порядка, чем волна НЕ11, соответствующая режиму передачи ООВ, при заданных величинах dс, Δ и λ.
Таким образом, требуется выбрать ООВ такое, которое, например, при рабочих длинах волн λ =1,3 или 1,55 мкм, будет работать в одномодовом режиме.
Для решения поставленной задачи в соответствии с (2.68) и табл. 2.3 составляем уравнение:
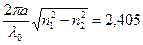 , (4.19)
, (4.19)
из которого определяется λ0 и сравнивается с рабочей длиной волны λр (1,3 или 1 55 мкм).
Например, при λр =1,3 мкм, необходимо, чтобы λ0 было меньше 1,3 мкм примерно на столько же (в относительных величинах), на сколько vp меньше, чем 2,405 в задаче по определению нормированной частоты.
Определение величины Δ многомодового ОВ. Целью расчета является определение величины Δ и, соответственно, разности ПП сердцевины и оболочки многомодового ОВ со ступенчатым ППП при заданных величинах числовой апертуры NА. Исходными данными являются числовая апертура NA, рабочая длина волны λ, ПП оболочки — n2.
Из (2.14), (2.66) и (2.12) имеем соотношения:
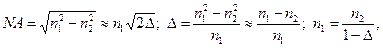
из которых получаем квадратное уравнение для определения величины Δ:
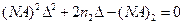
и соответственно
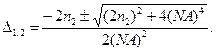 (4.21)
(4.21)
Физическому смыслу удовлетворяет первый корень этого уравнения.
Расчет числа мод в многомодовом ОВ. Целью расчета является определение числа существующих мод в многомодовом ОВ с диаметром сердцевины dс, заданной числовой апертурой NA на рабочей длине волны .
Число мод М определяется из следующего выражения:
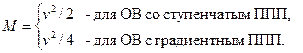
Определение уширения импульсов в ОВ. Как отмечалось в разд. 2.5.2 различие групповых скоростей модовых и спектральных компонент сигнала приводит к их дисперсии (рассеиванию во времени).
В импульсных системах передачи дисперсия вызывает искажение формы импульса, наиболее важным фактором которого является уширение импульса τ.В результате ограничивается допустимая скорость передачи сигнала. Различие групповых скоростей мод обуславливает модовую (межмодовую) дисперсию, различие групповых скоростей спектральных составляющих — хроматическую (внутримодовую) дисперсию.
Как отмечалось ранее, в свою очередь хроматическая дисперсия складывается из дисперсии материала и волноводной дисперсии.
Дисперсия материала определяется непостоянством величины ПП на различных длинах
волн, а отсюда vГР(λ)=с/n(λ); здесь и далее используются приближенные выражения [1; 5].
Волноводная дисперсия происходит вследствие нелинейности фазочастотной характеристики ОВ как оптического волновода.
Общее уширение импульсов при передаче по ОВ:
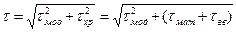 , (4.22)
, (4.22)
где τмод, τхр, τмат, τвв — уширение импульсов, обусловленное соответственно модовой и хроматической дисперсией, состоящей из дисперсии материала и волноводной дисперсии.
В многомодовых ОВ τмод>> τхр, поэтому согласно (2.102)
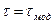 . (4.23)
. (4.23)
В одномодовых ОВ τмод = 0, поэтому согласно (2.103)
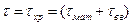 . (4.24)
. (4.24)
Соотношение уширения импульсов (τ), уширения, определенного по уровню 0,5 от максимальной амплитуды (τ0,5), и среднеквадратичного уширения (σ) приведено на рис. 4.3:
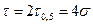

 Уширение импульса в МОВ с ростом длины линии возрастает вначале линейно, т.е. пропорционально L, а затем — пропорционально
Уширение импульса в МОВ с ростом длины линии возрастает вначале линейно, т.е. пропорционально L, а затем — пропорционально 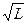 . Последняя закономерность объясняется взаимодействием и «перемешиванием» мод в результате наличия нерегулярностей в ОВ и в полной мере проявляется после прохождения сигналом расстояния, называемого длиной установления равновесия мод ОВ — Ly (разд. 2.5).
. Последняя закономерность объясняется взаимодействием и «перемешиванием» мод в результате наличия нерегулярностей в ОВ и в полной мере проявляется после прохождения сигналом расстояния, называемого длиной установления равновесия мод ОВ — Ly (разд. 2.5).
Расчетные формулы для определения τ в МОВ со ступенчатым ППП и с градиентным ППП представлены выражениями:
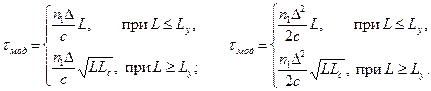 (4.25)
(4.25)
Уширение импульсов в ООВ с увеличением L растет линейно, оно зависит не только от параметров ОВ, но и от ширины спектра источника излучения Δλ. Полная ширина спектр источника, ширина спектра, определенная по уровню 0,5 от максимальной амплитуды, и среднеквадратичная ширина находятся в соотношении:
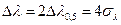 . (4.26)
. (4.26)
Расчетная формула для определения τ в ООВ представляется выражением (2.103), где τвв из (2.94), а τмат из (2.96).
Расчет пропускной способности ОК. Рабочая полоса частот (полоса пропускания) ОК определяет число передаваемых по нему каналов связи и определяется дисперсией ОВ.
Как известно, ширина полосы пропускания обратно пропорциональна уширению импульсов:
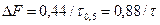 . (4.27)
. (4.27)
Как следует из (2.94), (2.96), (4.25) и (4.27) полоса пропускания одномодовых ОВ уменьшается по закону 1 / L, многомодовых ОВ — при L ≤ Ly — по закону 1 / L> а при L > Ly - пo закону 1 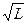 . В качестве примера можно определить максимально возможное число каналов передачи Nк по ОВ с шириной полосы пропускания ΔF. Для этого следует принять удельную скорость передачи информации по ОВ равной 1 бит/с на 1 Гц полосы частот. Известно, что для передачи аналогового звукового сигнала (полоса частот до 4 кГц) в импульсной (цифровой) форме необходимо произвести дискретизацию, уплотнение дискретизированных импульсов и аналого-цифровое преобразование, т.е. кодирование импульсов разных каналов. Число дискретизированных импульсов для одного телефонного канала может быть представлено в виде n=2fmax=2·400=8000. При кодировании импульсов, полученных в результате дискретизации, их амплитуда изменяется и заменяется ближайшей величиной в двоичном коде (квантование). Каждый уровень квантования представляется восьмиразрядным двоичным числом (т.е. имеется 28=256 возможных уровней квантования) и преобразуется в бинарные электрические (а затем в оптические) импульсы.
. В качестве примера можно определить максимально возможное число каналов передачи Nк по ОВ с шириной полосы пропускания ΔF. Для этого следует принять удельную скорость передачи информации по ОВ равной 1 бит/с на 1 Гц полосы частот. Известно, что для передачи аналогового звукового сигнала (полоса частот до 4 кГц) в импульсной (цифровой) форме необходимо произвести дискретизацию, уплотнение дискретизированных импульсов и аналого-цифровое преобразование, т.е. кодирование импульсов разных каналов. Число дискретизированных импульсов для одного телефонного канала может быть представлено в виде n=2fmax=2·400=8000. При кодировании импульсов, полученных в результате дискретизации, их амплитуда изменяется и заменяется ближайшей величиной в двоичном коде (квантование). Каждый уровень квантования представляется восьмиразрядным двоичным числом (т.е. имеется 28=256 возможных уровней квантования) и преобразуется в бинарные электрические (а затем в оптические) импульсы.
Таким образом, для передачи информации одного канала требуется 8000x8=64000 импульсов. Принимая в качестве средней скорости передачи в одном цифровом канале тональной частоты величину 70000 бит/с = 70 кбит/с, получаем максимально возможное число передаваемых каналов Nк при ширине пропускания F мГц:
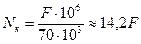 (4.28)
(4.28)
Для организации телефонных каналов в количестве, определенном (4.28), необходимо иметь два ОВ (каждое ОВ обеспечивает передачу сигналов в одном направлении).
Расчет коэффициента затухания ОВ. В разделе 2.5 рассмотрен коэффициент затухания в оптическом волокне вызванный потерями на рассеяние (2.76), потерями в материале (2.77), потерями обусловленными электронными и атомными резонансами в инфракрасной части спектра, aДД (2.78) и потерями на гидроксильных группах (2.82). Эти виды потерь образуют собственные потери волокна. Кроме собственных потерь в волокнах ОК появляются дополнительные или кабельные потери. Эти потери обусловлены структурой, деформациями и изгибами волокон, возникающими при наложении покрытий и защитных оболочек в процессе производства кабеля. К ним могут добавляться потери, возникающие при прокладке кабеля, например, изгибы кабеля, связанные с изменением направления трассы.
Для оценки дополнительных потерь вводят понятия макро – и микроизгибов ОВ (рис.4.4).

 Под макроизгибами понимают все макроскопические отклонения оси оптического волокна от прямой. Они возникают: 1) из-за изгиба кабеля при его намотке на кабельный барабан на заводе-изготовителе; 2) при прокладке и монтаже кабеля. Поэтому в ТУ на кабель всегда приводится минимально допустимый радиус изгиба кабеля. На рис. 4.4 а показано как на макроизгибе направляемая мода 1 превращается в вытекающую моду 2.
Под макроизгибами понимают все макроскопические отклонения оси оптического волокна от прямой. Они возникают: 1) из-за изгиба кабеля при его намотке на кабельный барабан на заводе-изготовителе; 2) при прокладке и монтаже кабеля. Поэтому в ТУ на кабель всегда приводится минимально допустимый радиус изгиба кабеля. На рис. 4.4 а показано как на макроизгибе направляемая мода 1 превращается в вытекающую моду 2.
Под микроизгибами понимают случайные микроскопические искривления, сопровождающиеся местными смещениями оси волокна на несколько микрометров (рис. 4.4 б). Микроизгибы волокна обусловлены локализованными поперечными нагрузками, распределенными по всей длине ОВ. Они могут быть результатом деформации ОВ в процессе изготовления и прокладки, а также изменениями геометрических размеров материалов элементов кабеля, которые вызваны вариациями температуры. Чувствительность к микроизгибам является функцией разности показателей преломления сердцевины и оболочки, а также диаметров сердцевины и оболочки [6, 7]. На рис. 4.4 б показан вариант возникновения микроизгибов, вызванных деформацией границы раздела сердцевина — оболочка ОВ. Микроизгибы могут вызывать значительные потери на излучение и взаимодействие мод.
Согласно [2] величина потерь на макроизгибах для многомодового ОВ определяется по выражению:
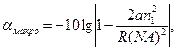 (4.29)
(4.29)
где αмакро — потери на макроизгибе, дБ; R — радиус макроизгиба в ОВ, мкм; а — радиус сердцевины ОВ, мкм; n1 — ПП сердцевины; NA — числовая апертура.
В [2] представлена формула, полученная экспериментальным путем сотрудником ВНИИКП м.н.с. Кремезом А.С. и позволяющая для МОВ с градиентным ППП при расчете добавочного затухания за счет макроизгиба (αмакро) учесть не только радиус кривизны оси ОВ, но и длину участка «искривления»:
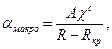 (4.30)
(4.30)
где αмакро — потери на макроизгибе, дБ; A – параметр, зависящий (в неявном виде) от числовой апертуры и диаметра сердцевины ОВ; R — радиус изгиба, мм; Rкр — постоянный параметр для данного типа ОВ, характеризующий радиус изгиба, при котором αмакро→∞ (из-за облома ОВ или полного «высвечивания» направляемых мод), мм; χ — число полных или неполных витков ОВ с радиусом изгиба; с — безразмерный параметр.
Для стандартного градиентного МОВ типа кварц-кварц с отношением радиусов сердцевины и оболочки a/b=50/ 25 (мкм); А=3,538; с =1/8; Rкр =2,2 мм.
Потери на макроизгибе для одномодового ОВ могут быть рассчитаны согласно [6] по выражению вида:
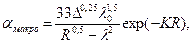 (4.31)
(4.31)
где αмакро — потери на макроизгибе, дБ; λ0 - длина волны отсечки, нм;
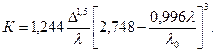
В табл. 4.1 приведены результаты расчетов αмакро по выражению (4.32), выполненные в [6].
Таблица 4.1. Результаты расчетов типовых значений потерь за счет макроизгибов в ОВ
| Тип ОВ | Рабочая длина волны, нм | Относительная разность ПП | Радиус микроизгиба, см | Потери на макроизгибе, дБ |
| Градиентное МОВ | 0,013 | 2,5 | 0,70 ... 1,20 | |
| 5,0 | 0,35 ... 0,60 | |||
| ООВ | 2,5 | 0,005 | ||
| 5,0 | 0,010 |
Величина потерь в кабеле вследствие микроизгибов ОВ может быть рассчитана согласно [6] по выражениям вида:
для многомодового ОВ
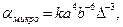 (4.32)
(4.32)
где αмикро— потери за счет изгибов в ОВ кабеля длиной 1 км, дБ; k — коэффициент зависит от амплитуды и периода микроизгибов; а и b — радиус сердцевины и оболочки ОВ соответственно, мкм;
для одномодового ОВ
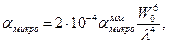 (4.33)
(4.33)
где 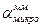 — потери в ОК на микроизгибах в МОВ, дБ/км; W0 — радиус модового поля, м; λ—длина волны, м.
— потери в ОК на микроизгибах в МОВ, дБ/км; W0 — радиус модового поля, м; λ—длина волны, м.
Выражение (4.33) является оценочным для определения требований к однородности ООВ.
Дата добавления: 2019-12-09; просмотров: 735;











