Ошибки наведения и вероятность поражения цели

Расчет динамической ошибки.Конечной задачей наведения снаряда является поражение цели. Поражение цели – случайное событие с вероятностью P_пор. P_пор следует иметь как можно большей. При условии, что снаряд доходит до конца управляемого участка, P_пор зависит от

- характеристики цели;

- вида боевого заряда;

- взрывателя;

- ошибок (промаха);

- величины «мертвой зоны» системы управления (СУ).

«Мертвая зона» - это зона, в которой определение расстояния между целью и снарядом становится невозможным, Причины образования «мертвой зоны» могут быть различны, например: недостаточная разрешающая способность, недостаточная маневренность снаряда, антенна смотрит мимо цели и т.п.

Под ошибкой наведения понимается различие параметров кинематической и фактической траекторий в момент прекращения работы СУ. Понятие промаха как линейной ошибки при наведении по направлению было рассмотрено и выражается в общем случае формулой (1.1).

PS. Понятие промаха r_пркак линейной ошибки при наведении по направлению может быть представлено в виде функциональной связи

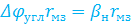, (1.1)

где - расстояние между целью и снарядом в момент выключения управления (расстояние мертвой зоны), а - угол наведения между вектором скорости снаряда и линией визирования в тот же момент. 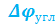- измеряемая угловая координата.

Кинематическая траектория (опорная) определяется методом наведения. Все объекты (цель, снаряд, пункт управления) - точки. Если учесть ограниченную маневренность снаряда и инерционность СУ, то получают динамическую траекторию.

Передаточная функция разомкнутого контура управления движением в одной плоскости при линейном представлении ЛА в общем случае имеет вид

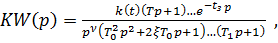(1.6)

где k(t) - коэффициент передачи всего контура,

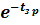- звено, отражающее запаздывание в линиях передачи информации.

Точное знание всей функции необходимо при определении устойчивости системы. При оценке точности этого не надо.

Среднее значение k(t) можно «заморозить», считая его постоянным на определенной дистанции, а также не учитывать характеристик рулевой машины, радиотехнических устройств из-за их малой инерционности по сравнению с инерционностью ЛА.

Если частота ω₀ собственных угловых колебаний корпуса ЛА относительно вектора скорости 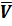значительно выше граничной частоты общего контура управления ω_к , то колебательный множитель в знаменателе может быть опущен. Передаточную функцию (1.6) можно заменить ее эквивалентом

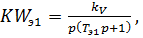(1.7)

или

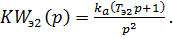(1.8).

Необходимым условием замены (1.6) одним из эквивалентов (1.7) или (1.8) является соблюдение равенства установившихся значений ошибок, т.е. сохранение порядка астатизма системы. Второе, желательное условие – соразмерность собственного периода колебаний и времени затухания переходного процесса в реальной и эквивалентной системах.

Ошибка управления в системе наведения (основное уравнение системы наведения как системы автоматического регулирования)

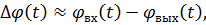(1.9)

где первое слагаемое 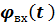– текущая координата кинематической траектории, второе 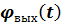- текущая координата динамической или фактической траектории.

В процессе движения объекта его кинематическая траектория изменяется и должна в каждый новый момент времени вычисляться от соответствующей точки на динамической траектории. Однако если управление по кинематической траектории происходит достаточно точно, эту особенность можно не учитывать и при расчетах ошибок пользоваться выражением (1.9) как равенством.

Функцию управления 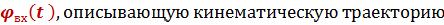в угловых или линейных координатах, в большинстве случаев описывают рядом по степеням (типовое воздействие в виде полиномиальной функции)

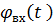= A₀+A₁t+A₂t²+……+A_ntⁿ… (1.10).

A₀ – начальное значение задающего воздействия; A₁ ( 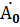)-начальная скорость изменения задающего воздействия; A₂- начальное ускорение, с которым изменяется задающее воздействие.

Тогда ошибка наведения

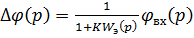(1.11)

может быть пре6дставлена в виде ряда

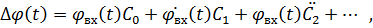(1.12)

где 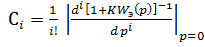- коэффициенты ошибок, - передаточная функция для ошибки по задающему воздействию.

Для систем с астатизмом первого порядка С₀=0 и ошибка по положению равна нулю. Для систем с астатизмом второго порядка С₀=С₁=0, т.е. отсутствуют ошибки по положению и скорости.

Число членов ряда (1.12) при выбранной управляющей функции для заданной траектории наведения и предполагаемого маневра цели определяется из условия

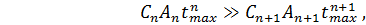(1.13)

где t_max- предварительно вычисленное максимальное значение времени движения ЛА до цели по кинематической траектории.

При известных t_max и n ошибка наведения определяется по формуле

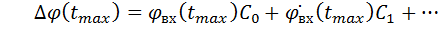(1.14)

Динамические ошибки тем больше, чем больше инерционность или постоянная времени системы управления.

Кроме динамической ошибки 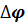в процессе наведения могут образовываться ошибки за счет воздействия ветра или воздушных течений. Когда скорость и направление ветра 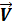известны и могут быть приняты постоянными, ошибки в одной плоскости движения рассчитываются по известным методам учета возмущающих воздействий в виде

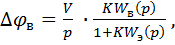(1.15)

где 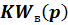- функция передачи части общего контура системы управления с функцией передачи 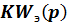от точки приложения вектора 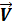до выхода из системы.

Если к входу системы приложены два воздействия: задающее 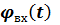и возмущающее v(t), причем взаимная корреляция между ними отсутствует, то средний квадрат результирующей ошибки Δφ определяется суммой двух составляющих ошибки по задающему воздействию и помехе

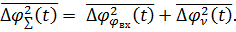(1.16)

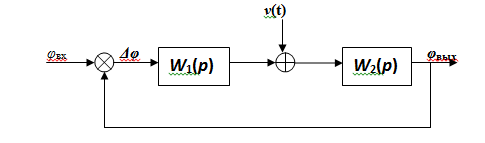
Рисунок 1.19 – Структурная схема СУ

Вспомним, что передаточная функция разомкнутой системы для схемы на рисунке 1.19,

W(p) = W₁(p) W₂(p).

Передаточная функция для ошибки по помехе

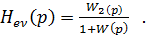
Передаточная функция замкнутой системы по ошибке e=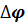

.

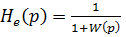Флюктуационная ошибка.Ошибки управления, вызванные случайными стационарными возмущениями и помехами Δφ_п

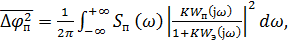(1.17)

где S_п(ω) – где спектральная плотность эквивалентных флюктуаций координаты системы управления в точке приложения, вызванных возмущениями или помехами, а 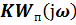- функция передачи системы от этой точки до выходной измеряемой координаты.

Флюктуационные ошибки уменьшаются с ростом инерционности системы, так как при большей инерционности системы улучшается сглаживание случайных возмущений.

Работа системы управления в конечном итоге характеризуется суммарной ошибкой наведения Δφ_∑ и вероятностью поражения цели. Для упрощения связи между ними используется понятие промаха, уже рассмотренное выше (формула (1.2)).

PS. r_пр = ψ · r_мз = 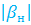· r_мз . (1.2)

Вероятность поражения. Положим, что ошибка наведения Δφ_нявляется случайной величиной со среднеквадратическим значением 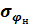и законом распределения вероятностей 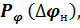тогда величина промаха r_ц – тоже случайная величина со среднеквадратическим значением

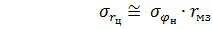(1.18)

и законом распределения вероятностей 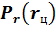. Если известен закон поражения цели, т.е. задана вероятность поражения цели 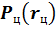как функции промаха, то вероятность поражения можно найти по формуле

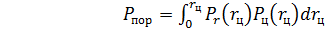(1.19)

Пример.

1) Возьмем нормальный закон распределения ошибок наведения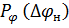

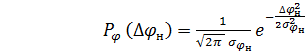. (1.20)

2) Закон поражения цели задан условиями

;

.

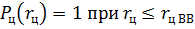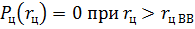Учитывая (1.20), определяем закон распределения вероятностей для величины промаха

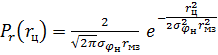при r_ц ≥ 0,

(1.21)

.

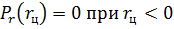Подставив (1.21) в (1.19), получим

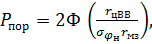(1.22)

где - (1.23)

интегральная функция.

С помощью формулы (1.22), задаваясь 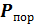цели, можно определить допустимое среднеквадратическое значение ошибки наведения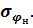

Если прекращение работы СУ совпадает с моментом взрыва, т.е. мертвой зоны нет, то понятие промаха и ошибки наведения совпадают, а вероятность поражения цели зависит только от линейных составляющих ошибки наведения.

[1] Сокращение вв обозначает взрыватель