Координаты и время.

Основные представления и понятия классической электродинамики.

Основные понятия.

Основными понятиями современной классической теории электромагнетизма являются понятие электрического заряда 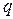и понятие электромагнитного поля.

Электрический заряд 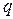является скалярной величиной и может иметь положительное или отрицательное значение. Величина электрического заряда является инвариантом относительно преобразований Лоренца: во всех инерциальных системах отсчета эта величина одинакова (масса тела этим свойством не обладает). В некоторых физических явлениях приходится учитывать дискретность (“квантованность”) электрического заряда, то есть учитывать, что электрический заряд тела состоит из конечного числа мельчайших элементарных зарядов. Элементарный электрический заряд численно равняется заряду электрона

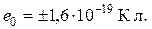
В классической динамике имеет место закон сохранения электрического заряда. Электрические заряды (движущиеся и неподвижные) формируют в пространстве электромагнитное поле, которое проявляется в силовом воздействии на материальные тела, обладающие электрическим зарядом или в которых имеет место движение электрических зарядов. Электромагнитное поле существует как объективная реальность и обладает такими атрибутами как масса, импульс и энергия. Электромагнитное поле может превращаться в вещество - рождение электронно-позитронных пар - и может порождаться веществом - аннигиляция электронно-позитронной пары.

В основе современных представлений о поле в классической электродинамике лежат два принципа: принцип локальности и принцип близкодействия. Согласно принципу локальности характеристики поля и соотношения связи между физическими величинами определяются в каждой точке области, в которой существует или рассматривается поле, и в каждый момент времени. При необходимости определения некоторых физических величин используется понятие малой окрестности рассматриваемой точки пространства. Согласно принципу близкодействия выделенный малый элемент электромагнитной системы (поля) непосредственно взаимодействует только с малыми элементами системы, составляющими его ближайшее окружение. Следствием обсуждаемого принципа является конечная величина скорости распространения сигнала в пространстве. Принцип близкодействия является альтернативой принципу дальнодействия, согласно которому имеет место взаимодействие, например, пространственно разделенных электрических зарядов. Как правило, считают, что закон всемирного тяготения Ньютона в механике и закон Кулона в электростатике являются выражением принципа дальнодействия. Скорость распространения сигнала в таких физических моделях бесконечно велика. Справедливости ради заметим, что в механике сплошных сред, также основанной на представлениях Ньютона, (в частности, в теории упругости, газовой динамике, акустике и т.д.), с успехом используется принцип близкодействия (принцип локальности взаимодействия элементарных объёмов среды), скорость распространения звуковых волн при этом – конечная величина.

Современный математический аппарат теории электромагнитного поля (принцип близкодействия) хорошо развит, он базируется на локальных (дифференциальных) соотношениях с частными производными, векторном анализе и тензорном исчислении, включает в себя вариационное исчисление с формулированием вариационных принципов и математическую теорию групп. Успехи вычислительной математики в немалой степени способствуют расширению области возможных практических приложений и проверке теоретических гипотез в рамках вычислительного эксперимента. Перечисленные математические методы органически связаны с физической природой электромагнитного поля.

Силовое воздействие на материальную точку можно определить, используя второй закон Ньютона:

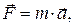(1)

где 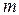- масса, 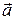- ускорение материальной точки. Соотношения кинематики

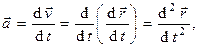(2)

где 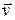- скорость, 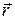- радиус-вектор материальной точки, позволяют по наблюдениям закона движения материальной точки 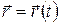определить величину 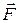в уравнении (1).

Фундаментальным теоретическим результатом анализа совокупности известных опытных фактов является выражение для обобщенной силы Лоренца:

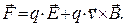(3)

Здесь 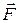- сила, действующая на материальную точку с зарядом 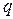, 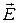- напряженность электрического поля, 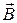- индукция магнитного поля. Силовые характеристики электромагнитного поля 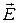и 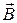- определяются в каждой точке пространства и могут зависеть от времени:

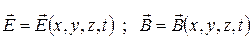(4)

В соотношении (3) подразумевается, что величины 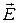и 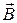вычисляются для фиксированного момента времени 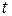в точке расположения электрического заряда 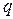. При этом напряженность электрического поля 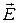и индукция магнитного поля 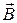представляют собой составляющие электромагнитного поля, внешнего по отношению к заряду 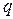. Смысл сказанного состоит в том, что предполагается, что электромагнитное поле, создаваемое самим зарядом 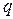, на заряд 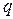не действует. Другими словами говоря, поле 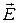и поле 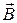в соотношении (3) созданы другими зарядами, неподвижными или движущимися. Из соотношения (3) следует, что напряженность электрического поля 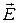- это та часть (составляющая) электромагнитного поля, которая связана с местонахождением «пробного» заряда, в то время как индукция магнитного поля 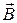связана со скоростью движения «пробного электрического заряда».

Из сказанного выше следует, что пространственные и временные изменения электрического поля 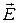и магнитного поля 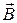должны быть согласованы между собой, должны учитывать распределение и движение электрических зарядов и, наверное, учитывать электромагнитные свойства среды, в которой рассматривается описываемое явление. Действительно, существует замкнутая система уравнений электродинамики - система уравнений Максвелла (время её создания 1855-1865 г.г.) - она достаточно сложна, с ней мы познакомимся в конце курса. Одно из достоинств системы уравнений Максвелла состоит в том, что она сохраняет форму записи во всех инерциальных системах отсчета. Говорят, что она инвариантна относительно преобразований Лоренца, т.е. согласуется с представлениями специальной теории относительности Эйнштейна.

Координаты и скорость материальной точки в двух различных инерциальных системах отсчета, естественно, различны, поэтому деление единого электромагнитного поля на электрическое поле и магнитное поле имеет условный характер, хотя и является удобным приемом при проведении практических расчетов.

В классической теории электромагнитного поля (рассматриваемой в настоящем учебном пособии) используется макроскопический (феноменологический) уровень описания. Физические величины, описывающие состояние «физически бесконечно малого объёма», являются осредненными макроскопическими величинами, полное изучение микроскопических величин связано с необходимостью использовать методы квантовой механики и статистики. Основу микроскопического описания электромагнитного поля, в котором учитывается положение и скорость каждого точечного электрического заряда, входящего в атом или молекулу, составляют уравнения Х. Лоренца, полученные им в 1902 году. В отдельных случаях (ниже некоторые из них будут рассмотрены) к успеху приводят методы элементарной молекулярно-кинетической теории вещества (теория Друде, время создания - 1900г.).

В современной теоретической физике существует несколько эквивалентных форм записи основных уравнений классической электродинамики – система уравнений Максвелла, система уравнений для скалярного и векторного потенциалов электромагнитного поля, вариационная формулировка и тензорная форма уравнений электродинамики. Первичные сведения об этих представлениях содержатся в соответствующих разделах настоящего курса. С более глубоким содержанием этих представлений можно ознакомиться по учебникам теоретической физики.

Координаты и время.

Понятия “пространство” и “время” ниже используются как первичные понятия современной физики.

Точка пространства в определённый момент времени является простейшей математической структурой, связанной с рассматриваемыми понятиями. Её описание становится определённым, если выбрана система отсчета (т. е. совокупность тела отсчёта, системы координат и “часов” системы отсчета). Следует помнить, что не существует “абсолютной”, вросшей в пространство и не связанной с материальными телами системы отсчёта. В пространстве трёх измерений положение точки пространства может быть задано тремя координатами, их значения относятся к моменту времени, который отсчитывается по “часам” системы отсчета.

Существует множество различных систем координат: прямолинейные (косоугольные и ортогональные), криволинейные (общие криволинейные и ортогональные криволинейные).

Чаще других используются прямолинейные ортогональные (декартовы) системы координат и криволинейные ортогональные системы координат, например, цилиндрические или сферические. Специальные системы координат удобно применять в прикладных исследованиях, когда форма исследуемой области описывается уравнениями координатных поверхностей или тип симметрии рассматриваемой задачи совпадает с типом симметрии координатной системы. Система декартовых координат обладает определёнными преимуществами, как в общетеоретическом, так и в практическом плане, поскольку декартовы координаты проще всего связаны с длинами и расстояниями. Эта система координат и будет преимущественно использоваться ниже.

Система декартовых координат определена, если известно положение точки О - начала координат, выбраны три взаимно перпендикулярные направления (координатные линии) и фиксированы их обозначения, например x, y и z ; на всех трёх координатных линиях введён один и тот же масштаб измерения, постоянный для любого заданного отрезка координатной линии. В этом случае о проекции точки пространства на координатную ось можно говорить в двух смыслах - как о точке координатной линии, или как о численной величине проекции, соответствующей отсчету в принятом масштабе измерения, связанному с этой точкой.

Если рассмотреть в пространстве две точки А и В и их проекции А¢ и В¢ на выбранную координатную линию, то проекцией отрезка АВ на эту линию можно считать отрезок А¢В¢ координатной линии (геометрический подход), или разность отсчетов координат В¢ - А¢ (алгебраический поход). Только в декартовой системе координат длина отрезка А¢В¢ (с учётом выбранного масштаба длины) совпадает с абсолютной величиной разности отсчетов координат соответствующих точек В¢- А¢.

Описание системы отсчета включает в себя постулат о равномерности хода “часов” системы отсчёта и возможности выбора соответствующей единицы измерения времени. Проблема синхронизации часов, расположенных на расстоянии s друг от друга, решается по Эйнштейну условием, что сигнал от источника в точку наблюдения попадает через промежуток времени d t, равный отношению величины s к скорости света c в вакууме.

Таким образом, переменные x, y, z, t (декартовы координаты и время) вполне определяют положение точки в пространстве в заданный момент времени, если выбрана (фиксирована) система отсчета. Ниже рассматриваются только инерциальные системы отсчета и «правые», чаще всего декартовы системы координат.

Скаляр и вектор.

Физические величины различной природы могут иметь различную математическую структуру и, соответственно, различные математические правила их использования.

Скалярная величина является одной из простейших математических структур. Алгебра скалярных величин установлена достаточно давно, хотя и далеко не сразу. Так у древних греков не было понятия «нуль», позже были трудности с осознанием смысла отрицательных величин. Мнимые величины появились в 1545 г. в трудах итальянского математика Дж. Кардано, которого считали чуть ли не сумасшедшим: число, умноженное само на себя и вдруг отрицательное? Такого не может быть! Прошло время. Современные математики не мыслят математики без комплексных чисел.

Ещё Архимед, который жил в 287-212 г.г. до н.э., складывал силы, действующие на тело, по правилу параллелограмма. Строгого определения понятия «вектор» в те далёкие годы ещё не было, но интуитивно Архимед рассматривал объекты, характеризующиеся не только величиной, но и направлением.

Голландский математик и инженер С. Стевин (1548-1620) считается создателем понятия «векторная величина»: он заново открыл правило сложения сил, известное Архимеду. Через сто лет великий Исаак Ньютон (1642-1727) в монографии «Математические начала натуральной философии» (основа классической механики Ньютона) ещё раз сформулировал правило параллелограмма наряду с формулировками первого, второго и третьего законов механики.

Термин «вектор» (от латинского «vector» - несущий) придумал в 1845 г. ирландский математик У.Р. Гамильтон (1805-1865), он же предложил термин «скаляр», строго определил операции «скалярное произведение» и «векторное произведение». Выдающиеся результаты в теории объектов сложной математической структуры принадлежат Г. Грассману (1809-1877), У. Клиффорду (1845-1879) и Дж. У. Гиббсу (1839-1903). Геометрическое изображение вектора как направленного отрезка появилось, как полагают, у Гамильтона. В 1853 г. французский математик О. Коши (1789-1857) ввёл в научный обиход понятие «радиус-вектор» и соответствующее ему обозначение .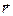

Из элементарного курса известны простейшие определения скаляра (скалярной величины) и вектора (векторной величины):

¾ скаляром называется величина, которая при определенном выборе единицы измерения однозначно характеризуется числом, ее измеряющим;

¾ вектор определяется своей величиной (модулем) и направлением в пространстве и складывается с другим вектором той же физической размерности по правилу треугольника или параллелограмма.

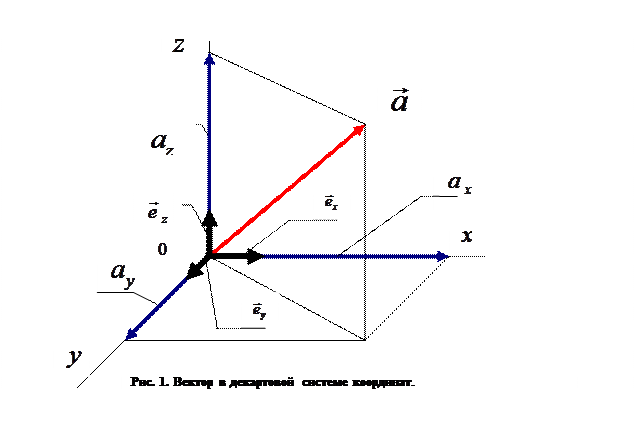
Для описания вектора в трехмерном пространстве (рис. 1) необходимо одновременно задать три параметра (три проекции, или модуль вектора и углы между направлением вектора и какими-либо двумя из трех координатных направлений). Очевидное различие в математических структурах скалярной и векторной величин приводит к различию в свойствах указанных объектов.

Строгая классификация физических объектов основана на изучении характера изменения их компонент при преобразованиях систем координат (т.е. при переходе от одной координатной системы к другой). В физике чаще всего имеют дело с преобразованиями систем координат в обычном трехмерном пространстве или в четырехмерном пространстве-времени Г. Минковского. Трансформационные свойства физических величин могут быть различны в этих случаях. К примеру, кинетическая энергия материальной точки — скаляр относительно преобразований системы координат в трехмерном пространстве и одна из компонент 4-вектора относительно преобразований в пространстве Минковского.

Важно отметить, что и вид преобразований системы координат может оказаться существенным. Так “вращения” и “сдвиги” координатных систем отличаются тем, что «вращения» переводят “правые” координатные системы в “правые”, а «отражение» относительно одной из координатных поверхностей переводит «правую» координатную систему в «левую». Физическая величина может оказаться инвариантной (неизменной) при преобразовании «вращения» и неинвариантной при преобразовании «отражения».

При изучении преобразований систем координат в основной части курса мы ограничимся преобразованиями сдвига и вращения правых декартовых систем координат.

В общем, указание трансформационных свойств физической величины (т.е. ее тензорного характера) имеет смысл только по отношению к определенной группе преобразований координат в данном пространстве. С рассматриваемой точки зрения,

скаляр — это величина, инвариантная относительно (разрешенных) преобразований координат,

вектор — совокупность компонент, которые при преобразовании координат трансформируются по определённому правилу,

с этим правилом мы познакомимся ниже. Многокомпонентные объекты более сложной математической структуры, чем вектор, описаны в курсах тензорного исчисления и высшей алгебры и используются при рассмотрении соответствующих физических понятий и моделей.

Ниже для описания скалярной величины или функции используются общепринятые обозначения. Векторные величины принято описывать или в символической форме (т.е. без указания конкретной системы координат), например, вектор 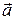, или в координатной форме 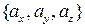, где упорядоченные величины в фигурных скобках представляют собой проекции вектора 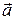на соответствующие координатные линии декартовой системы координат. В векторном анализе употребляется понятие «составляющие вектора». При этом имеют в виду векторы 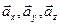, на рисунке 1 они показаны направленными стрелками, но не обозначены. Операции сложения, вычитания, скалярного и векторного умножения векторов и их геометрическая интерпретация предполагается известными из курса математики.