Минимизация функций. Карты Карно
Исследование функционирования логических элементов и комбинационных схем
Логические функции
Любое логическое выражение, составленное из п переменных Хn-1, X n-2 … X 0 с помощью конечного числа операций алгебры логики, можно рассматривать как некоторую функцию п переменных. Такую функцию называют логической. В соответствии с аксиомами алгебры логики функция может принимать в зависимости от значения переменных значение 0 или 1. Функция n логических переменных может быть определена для 2n значений переменных, соответствующих всем возможным значениям n-разрядных двоичных чисел.
Основной интерес представляют следующие функции двух переменных х и у:
fl (x, у) = х×у - логическое умножение (конъюнкция),
f2 (x, у) = хÚу - логическое сложение (дизъюнкция),
f3 (x, у) = 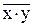 - логическое умножение с инверсией,
- логическое умножение с инверсией,
f4 (x, у) = 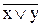 - логическое сложение с инверсией,
- логическое сложение с инверсией,
f5 (x, y) = xÅy=x`yÚ`xy - суммирование по модулю 2,
f6 (x, у) = 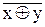 = хуÚ
= хуÚ 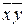 - равнозначность.
- равнозначность.
Логические схемы
Физическое устройство, реализующее одну из операций алгебры логики или простейшую логическую функцию, называется логическим элементом. Основным логическим функциям соответствуют выполняющие их логические элементы (ЛЭ).
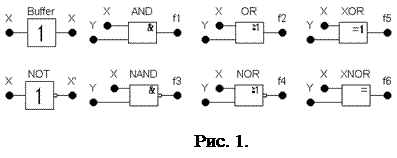 |
Условные графические обозначения (УГО) ЛЭ, выполненные в соответствии с требованиями ЕСКД, представлены на рис.1.
На рисунке изображены следующие ЛЭ:
-Buffer (Повторитель) реализует функцию f(x)=x;
-NOT (элемент НЕ, инвертор), реализует функцию инвертирования f(x)=`x;
-AND (элемент И) реализует функцию логического умножения (конъюнкции) f1;
-NAND (элемент И-НЕ) реализует функцию инверсии логического умножения f3;
-OR (элемент ИЛИ) реализует функцию логического сложения (дизъюнкции) f2;
-NOR (элемент ИЛИ-НЕ) реализует функцию инверсии логического сложения f4;
-XOR элемент реализует функцию суммирования по модулю 2 f5;
-XNOR элемент реализует функцию равнозначности f6.
Схема, составленная из конечного числа логических элементов по определенным правилам, называется логической схемой.
Логическая схема, выходные сигналы F которой описываются логической функцией
F = f(xn-1, xn-2, …, хj, … x0),
где хj – входные сигналы логической схемы, j=0, 1, …, n-1, называется комбинационной схемой (КС).Комбинационная схема реализует однозначное соответствие между значениями входных и выходных сигналов.
Таблицы истинности
Так как область определения любой функции п переменных конечна (2n значений), такая функция может быть задана таблицей значений fi, которые она принимает на наборах переменных с номерами j = 0, 1, …,2n-1.
Такие таблицы называют таблицами истинности. В табл.1 представлены таблицы истинности, задающие указанные выше функции.
| Таблица 1 | ||||||||
| Номер набора j | Значения переменных | Значения функции | ||||||
| X | У | fl | f2 | f3 | f4 | f5 | f6 | |
Минимизация функций. Карты Карно
Если число логических переменных не превышает 5-6, преобразования логических функций удобно производить с помощью карт Карно. Цель преобразований - получение компактного логического выражения (минимизация). Минимизацию производят объединением наборов (термов) на карте Карно. Объединяемые наборы должны иметь одинаковые значения функции (все 0 или все 1).
Для наглядности рассмотрим пример: пусть требуется найти логическое выражение для мажоритарной функции fm трех переменных X, Y, Z, описываемой следующей таблицей истинности:
| Таблица 2 | ||||
| j | X | Y | Z | fm |
Составим карту Карно. Она представляет собой нечто похожее на таблицу, в которой наименования столбцов и строк представляют собой значения переменных, причем переменные располагаются в таком порядке, чтобы при переходе к соседнему столбцу или строке изменялось значение только одной переменной. Например, в строке XY табл. 3 значения переменных XY могут быть представлены следующими последовательностями: 00, 01, 11, 10.Таблицу заполняют значениями функции, соответствующими комбинациям значений переменных. Полученная таким образом таблица выглядит, как показано ниже (табл.3).
| Таблица 3 | ||||
| xy z |  10 10
| |||
 0 0
| ||||
На карте Карно контурами отмечаем группы, состоящие из 2i ячеек (2, 4, 8,...) и содержащие 1, т. к. они описываются простыми логическими выражениями. Три контура в таблице определяют логические выражения XY, XZ, YZ. 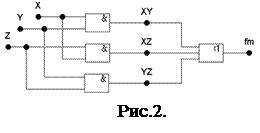 Компактное выражение, описывающее функцию, представляет собой дизъюнкцию полученных при помощи карт Карно контермов. В результате получаем выражение в дизъюнктивной нормальной форме(ДНФ): fm = XY Ú XZ Ú YZ.Для реализации функции мажоритарной логики трех логических переменных необходимо реализовать схему, которая при подаче на ее входы трех сигналов формировала бы на выходе сигнал, равный сигналу на большинстве входов (2 из 3 или 3 из 3). Схемная реализация заданной минимизированной функции в булевом базисе приведена на рис.2.
Компактное выражение, описывающее функцию, представляет собой дизъюнкцию полученных при помощи карт Карно контермов. В результате получаем выражение в дизъюнктивной нормальной форме(ДНФ): fm = XY Ú XZ Ú YZ.Для реализации функции мажоритарной логики трех логических переменных необходимо реализовать схему, которая при подаче на ее входы трех сигналов формировала бы на выходе сигнал, равный сигналу на большинстве входов (2 из 3 или 3 из 3). Схемная реализация заданной минимизированной функции в булевом базисе приведена на рис.2.
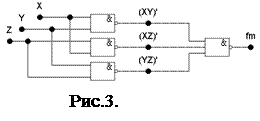 Для реализации функции на элементах И-НЕ преобразуем полученное выражение в базис элементарных функций И-НЕ, т. е. Выполним тождественное преобразование исходного логического выражения при помощи операций двойной инверсии:
Для реализации функции на элементах И-НЕ преобразуем полученное выражение в базис элементарных функций И-НЕ, т. е. Выполним тождественное преобразование исходного логического выражения при помощи операций двойной инверсии:
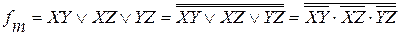 .
.
Проверить справедливость каждого из приведенных выражений для fm можно прямой подстановкой значений X, Y, Z из табл.2.
Соответствующая схемная реализация приведена на рис.3.
Дата добавления: 2017-06-13; просмотров: 2499;











