Исследование устойчивости систем автоматического регулирования
План лекции:
1. Общие соображения об устойчивости систем.
2. Алгебраический критерий Гурвица.
3. Частотный критерий Найквиста.
Литература: [2], [3].
1. Одной из основных задач теории автоматического регулирования является изучение динамических процессов, происходящих в автоматически системах. Автоматические системы при нормальной эксплуатации должны поддерживать определенный режим работы объекта регулирования при действии на него многих возмущающих факторов. Такое поведение может быть достигнуто лишь в системах автоматического регулирования, обладающих устойчивостью по отношению к этим воздействиям. Устойчивость – это свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия.
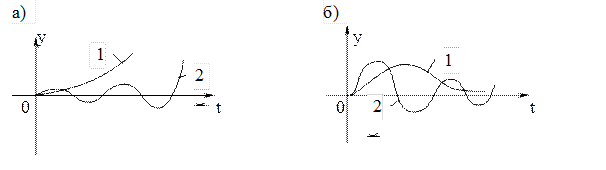
Рис.14
На рис.14 показаны типичные кривые переходных процессов в неустойчивой (рис.14, а) и устойчивой (рис.14, б) системах. Если система неустойчива, то достаточно любого толчка, чтобы в ней начался расходящийся процесс ухода из исходного установившегося состояния. Этот процесс может быть апериодическим (кривая 1 на рис.14, а) или колебательным (кривая 2 на рис. 14, а). Апериодический расходящийся процесс может, например, возникнуть в САР, если в ее управляющем устройстве (регуляторе) ошибочно переключить полярность воздействия на объект, в результате чего управляющее устройство будет осуществлять не отрицательную, а положительную обратную связь вокруг объекта. При этом управляющее устройство будет не устранять отклонение y, а действовать в обратном направлении, вызывая лавинообразное его изменение. Колебательный расходящийся процесс может наступить, например, при неограниченном увеличении коэффициента передачи системы, вследствие чего управляющее устройство станет излишне энергично воздействовать на объект, стремясь ликвидировать первоначально возникшее отклонение y. В этом случае при каждом очередном возврате y к нулю под действием устройства кривая l будет пересекать ось абсцисс все с большей скоростью и процесс в целом будет расходящимся.
В случае устойчивой системы (рис.14, б) переходный процесс, вызванный каким-либо воздействием, со временем затухает апериодически (кривая 1) или колебательно (кривая 2), и система вновь возвращается в установившееся состояние.
Таким образом, устойчивую систему можно определить также как систему, переходные процессы в которой являются затухающими.
2. Поскольку процессы в системах автоматического регулирования описываются дифференциальными уравнениями, то математический анализ устойчивости сводится к исследованию свойств решения таких уравнений. Для суждения об устойчивости системы практически не требуется решать эти уравнения в связи с тем, что разработаны косвенные признаки, по которым можно судить об устойчивости системы. Эти косвенные признаки называются критериями устойчивости и опираются на вид корней характеристический уравнений систем. Действительно, решение любой линейной системы дифференциальных уравнений может быть представлено в следующем виде:
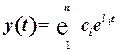 , (29)
, (29)
где 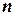 – порядок системы
– порядок системы
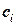 – произвольные постоянные, зависящие от конечных возмущений и начальных условий
– произвольные постоянные, зависящие от конечных возмущений и начальных условий
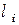 – корни характеристического уравнения степени.
– корни характеристического уравнения степени.
Необходим и достаточным условием устойчивости решения (29) является отсутствие корней 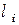 с положительными вещественными частями. Если таких корней нет, то
с положительными вещественными частями. Если таких корней нет, то 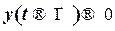 – система устойчива. Если имеется хотя бы один корень с положительной вещественной частью, то
– система устойчива. Если имеется хотя бы один корень с положительной вещественной частью, то 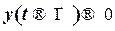 – система неустойчива. По существу, критерии устойчивости и определяют отсутствие подобных корней с положительными вещественными частями.
– система неустойчива. По существу, критерии устойчивости и определяют отсутствие подобных корней с положительными вещественными частями.
Наиболее распространены три основных критерия устойчивости: алгебраический критерий Рауса – Гурвица, частотные критерии Михайлова и Найквиста. Последние получили наиболее широкое применение, так как, во-первых, они позволяют судить об устойчивости замкнутой системы 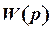 ; во-вторых, анализ устойчивости можно выполнять и по экспериментально определенным частотным характеристикам; в-третьих, с помощью частотных характеристик можно судить и о качестве переходных процессов в системах.
; во-вторых, анализ устойчивости можно выполнять и по экспериментально определенным частотным характеристикам; в-третьих, с помощью частотных характеристик можно судить и о качестве переходных процессов в системах.
Критерий устойчивости Гурвица. В разной форме этот критерий был предложен английским математиком Е.Раусом и затем швейцарским математиком А.Гурвицом в конце прошлого века. Приведем без доказательства этот критерий в форме Гурвица.
Для того, чтобы движение системы было устойчивым, необходимо, чтобы коэффициенты при всех членах дифференциального уравнения, описывающего переходный процесс системы, были отличны от нуля и имели одинаковые знаки. Необходимо также, чтобы некоторые определители 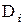 составленные из этих коэффициентов, были бы положительны.
составленные из этих коэффициентов, были бы положительны.
Переходный процесс линейной автоматической системы описывается дифференциальным уравнением системы без правой части (однородным уравнением).
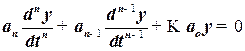 . (30)
. (30)
Уравнение (30) запишем в операторной форме
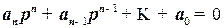 .
.
Полученное уравнение называется характеристическим уравнением линейной автоматической системы.
Очевидно, первое условие устойчивости сводится к требованию
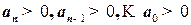 или
или 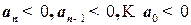 . (32)
. (32)
Для систем первого и второго порядка достаточно первого условия. Для систем третьего порядка 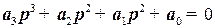 необходимы выполнение второго условия
необходимы выполнение второго условия
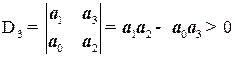 ; (33)
; (33)
т.е. произведение средних коэффициентов должно быть больше, чем произведение крайних.
Критерий устойчивости Найквиста. Был предложен в 1932 г. американским ученым Г.Найквистом. Этот критерий позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой частотной характеристике (а.ф.ч.х.) разомкнутой системы. Рассмотрим этот критерий для случая, когда известно, что система в разомкнутом состоянии устойчива. Условие устойчивости замкнутой системы тогда сводится к требованию, чтобы в.ф.ч.х. при увеличении 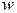 от 0 до
от 0 до 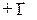 разомкнутой системы не охватывала бы точку
разомкнутой системы не охватывала бы точку 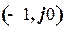 .
.
 .
.
Рис.15
На рис.15 характеристика 1 соответствует устойчивым системам, характеристика 3 – неустойчивой, а характеристика 2 – нахождению системы на границе устойчивости.
В соответствии с критерием Найквиста об устойчивости можно судить не только по а.ф.ч.х., но и совместно по а.ч.х. и ф.ч.х. Обычно при этом пользуются логарифмическими характеристиками, что представляет большое удобство в силу простоты их построения.
Согласно критерию Найквиста, для системы устойчивой в разомкнутом состоянии, условием устойчивости ее в замкнутом состоянии является неохват а.ф.ч.х. точки 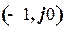 . Последнее имеет место, если при частоте, на которой
. Последнее имеет место, если при частоте, на которой 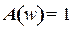 , абсолютное значение фазы меньше
, абсолютное значение фазы меньше 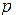 . Сказанное непосредственно следует из рис. 15. Таким образом, применительно к логарифмическим характеристикам, если учесть при этом, что значению
. Сказанное непосредственно следует из рис. 15. Таким образом, применительно к логарифмическим характеристикам, если учесть при этом, что значению 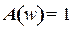 соответствует
соответствует 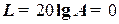 , критерий устойчивости Найквиста для систем, устойчивых в разомкнутом состоянии, сводится к тому, что л.а.х. должна пересечь ось абсцисс раньше, чем фаза, спадая, окончательно перейдет значение
, критерий устойчивости Найквиста для систем, устойчивых в разомкнутом состоянии, сводится к тому, что л.а.х. должна пересечь ось абсцисс раньше, чем фаза, спадая, окончательно перейдет значение 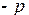 .
.
Изложенное иллюстрируется рис.16.
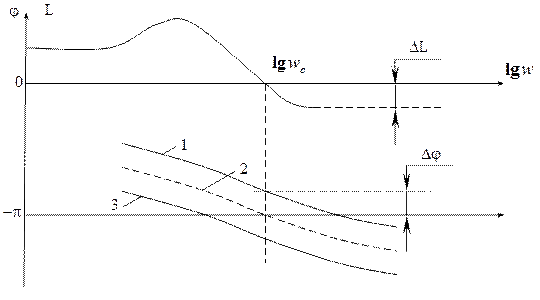
Рис.16.
Здесь изображены л.а.х. 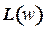 и три варианта л.ф.х..
и три варианта л.ф.х..
В случае л.ф.х. 1 система устойчива. л.ф.х 2 соответствует нахождению замкнутой системы на границе устойчивости, л.ф.х. 3 – неустойчивой замкнутой системе.
При оценке устойчивости систем одного факта устойчивости недостаточно. Необходимо еще оценить величину запаса устойчивости, т.е. степени удаленности системы от границы устойчивости. Система, которая теоретически является устойчивой, но находится очень близко к границе устойчивости, практически при ее реализации может оказаться неустойчивой как следствие неточности математического описания системы, использованного при оценке устойчивости, так и из-за изменения во времени параметров системы.
Основное распространение в качестве меры запаса устойчивости получили вытекающие из критерия Найквиста две величины – запас устойчивости по фазе 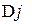 и запас устойчивости по амплитуде
и запас устойчивости по амплитуде 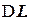 . Эти величины показаны на рис.16 для системы с л.ф.х., представленной с кривой L.
. Эти величины показаны на рис.16 для системы с л.ф.х., представленной с кривой L.
Запас устойчивости по фазе определяется величиной, на которую должно возрасти запаздывание по фазе в системе на частоте среза 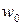 , чтобы система оказалась на границе устойчивости.
, чтобы система оказалась на границе устойчивости.
Запас устойчивости по амплитуде определяется величиной 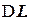 допустимого подъема л.а.х., при котором система окажется на границе устойчивости. Обычно выбирают запас устойчивости
допустимого подъема л.а.х., при котором система окажется на границе устойчивости. Обычно выбирают запас устойчивости 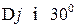 , а
, а 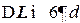 .
.
Дата добавления: 2022-05-27; просмотров: 214;











