Понятие о частотных характеристиках звеньев и систем

План лекции:

1. Частотные характеристики: амплитудно-частотная характеристика, фазово-частотная характеристика и амплитудно-фазовая частотная характеристика.

2. Связь между передаточной функцией системы и ее частотными характеристиками.

3. Логарифмические частотные характеристики.

Литература: [2], [3].

1. Частотными характеристиками называются зависимости, связывающие входную и выходную величины линейной системы или звена в установившемся режиме, когда входная величина изменяется по гармоническому закону. Допустим на вход устройства подано гармоническое воздействие

,

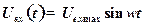где 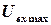– амплитуда, а 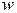– круговая частота этого воздействия. По окончании переходного процесса на выходе устройства будут существовать гармонические колебания с той же частотой, что и входные колебания, но отличающиеся в общем случае по амплитуде и фазе, т.е. в установившемся режиме выходная величина устройства

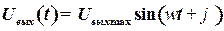
где 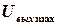– амплитуда выходных установившихся колебаний;

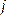– фазовый сдвиг между входными и выходными колебаниями.

При фиксированной амплитуде входных колебаний амплитуда и фаза установившихся колебаний на выходе устройства зависит от частоты колебаний. Если постепенно увеличивать от нуля частоту входных колебаний и определять установившиеся значения амплитуды и фазы выходных колебаний для различных частот, можно получить в зависимости от частоты отношение амплитуд

,

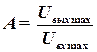и сдвиг 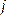выходных и входных установившихся колебаний. Эти зависимости называются соответственно 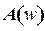– амплитудной частотной характеристикой (а.ч.х.) и 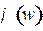– фазовой частотной характеристикой (ф.ч.х).

Амплитудную и фазовую частотные характеристики можно объединить в одну характеристику – амплитудно-фазовую частотную характеристику (а.ф.ч.х.). Амплитудно-фазовая частотная характеристика строится следующим образом. Усиление амплитуды 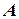представляется в виде вектора, откладываемого от оси абсцисс под углом, равным сдвигу фазы на каждой частоте. Соединяя концы всех векторов, получаем некоторую кривую, которая и является графиком амплитудно-фазовой характеристики (рис.11а).

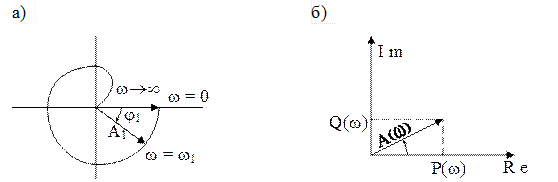
Рис.11

Амплитудно-фазовую частотную характеристику можно строить и в прямоугольной системе координат – в комплексной плоскости. При этом координатами будут показанные на рис.11б проекции P и Q вектора A на соответствующие оси. Зависимости P(w) и Q(w) называются соответственно действительной и мнимой частотными характеристиками.

2. Аналитические выражения для рассмотренных выше частотных характеристик могут быть легко получены по передаточной функции звена W(p), если оператор Лапласа P заменить оператором Фурье - jw, где: jw – комплексная круговая частота гармонического входного сигнала. В таком случае передаточная функция системы или звена может быть представлена комплексным выражением:

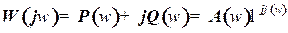, (18)

где 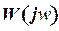– амплитудно-фазовая частотная характеристика;

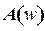– выражение для амплитудно-частотной характеристики звена, численно равное модулю ;

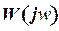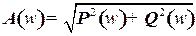. (19)

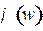– выражение для фазовой частотной характеристики звена, численно равное аргументу :

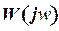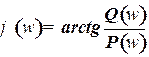. (20)

Чтобы проанализировать применение введенных понятий, рассмотрим инерционное звено, для которого имеем передаточную функцию в виде

.

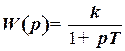Заменяя 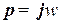, получим комплексную частотную характеристику

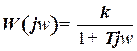. (21)

Для дальнейшего использования преобразуем выражение (21). Для этого умножим числитель и знаменатель на величину 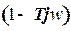и учитывая, что 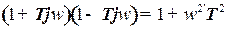, запишем

,

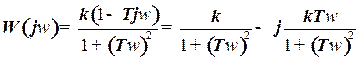где

; .

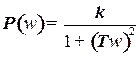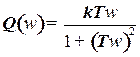Амплитудно-частотная характеристика будет

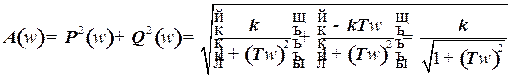(22)

а фазово-частотная характеристика

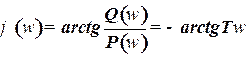. (23)

Графическая интерпретация соотношений (22), (23) и амплитудно-фазовой частотной характеристики представлена на Рис.12.

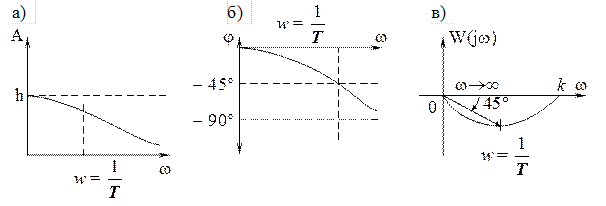
Рис.12

а), б) – амплитудно- и фазочастотные характеристики, в) – амплитудно-фазовая частотная характеристика.

Как видно, из амплитудно-частотной характеристики, инерционное звено хорошо пропускает колебания низкой частоты в плохо колебания высокой частоты.

Еще раз напомним, что связь между частотными характеристиками системы и составляющих ее звеньев определяется выражением для передаточной функции, если подставить в него .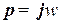

Соответственно амплитудно-фазовая частотная характеристика цепочки последовательно соединенных звеньев разомкнутой системы, согласно (13), имеет вид:

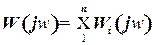, (24)

где 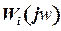- амплитудно-фазовая частотная характеристика i-го звена цепочки. Отсюда

,

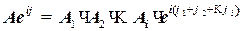т.е.

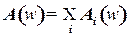. (25)

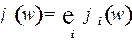, (26)

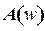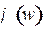где и – амплитудная и фазовая характеристики цепочки звеньев, а 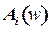и 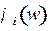– эти характеристики i-го звена.

Амплитудно-частотная характеристика цепочки звеньев равна произведению амплитудных частотных характеристик составляющих ее звеньев. Фазово-частотная характеристика цепочки звеньев равна сумме фазово-частотных характеристик составляющих ее звеньев.

3. При исследовании систем автоматического управления амплитудную и фазовую частотные характеристики удобно строить в логарифмических координатах. Если прологарифмировать выражение (25), получим

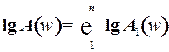; (27)

т.е. в логарифмическом масштабе амплитудная частотная характеристика цепочки звеньев равна сумме амплитудных характеристик отдельных звеньев. Амплитудная частотная характеристика в логарифмических координатах строится в виде зависимости 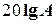от 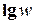, называемой логарифмической амплитудной характеристикой (л.а.х.), а фазовая в виде зависимости 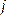от 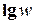, называемой логарифмической фазовой характеристикой (л.ф.х.). Величина 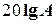обозначается L. В качестве единицы этой величины используется децибел, равный одной десятой бела. Бел – это единица десятичного логарифма коэффициента усиления мощности сигнала, т.е. 1 бел соответствует усилению мощности в 10 раз, 2 бела – в 100 раз, 3 бела – 1000 раз и т.д. Так как мощность сигнала пропорциональна квадрату амплитуды, а 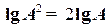, то усиление в белах, выраженное через отношение амплитуд, равно 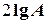. Соответственно в децибелах оно равно .

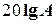В качестве примера рассмотрим построение л.а.х. для инерционного звена. (Инерционное звено можно представить в виде последовательного соединения пропорционального и единичного инерционного звеньев . Для этого прологарифмируем выражение (22):

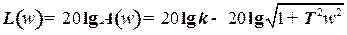. (28)

Логарифмическая амплитудная частотная характеристика рассматриваемого звена может быть приближенно представлена ломаной линией, которая показана на рис.13.

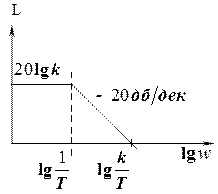
Рис.13.

Эта приближенная характеристика называется асимптотической л.а.х. Такое название связано с тем, что эта характеристика составлена из двух асимптот, к которым стремится л.а.х. пр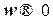и и 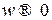. Найдем эти асимптоты. При малых значениях 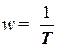в выражении (28):

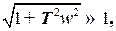т.е. .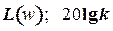

Соответственно характеристика представляет собой прямую параллельную оси абсцисс и проходящую на уровне 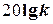. Это есть первая асимптота, к которой стремится л.а.х. при .

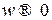С другой стороны, на больших частотах, когда 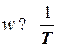в (28):

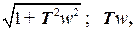т.е. ..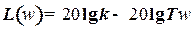

В этом случае характеристика представляет собой прямую, имеющую наклон – 20 дб/дек. Действительно, при увеличении 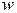на декаду, т.е. в 10 раз.

.

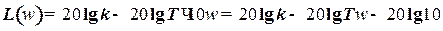Таким образом, величина 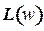уменьшилась на 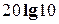, т.е. на 20 дб. Эта линия является второй асимптотой, к которой стремится л.а.х. при .

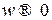Как видно из л.а.х., полоса пропускания частот инерционного звена лежит приблизительно в пределах .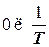

Заметим, что как передаточная функция, так и частотные характеристики описывают один и тот же процесс, одни и те же свойства системы с одинаковой плотностью. Применение той или иной характеристики для исследования системы зависит не столько от ее устройства, сколько от ее назначения и использования. Так, например, назначение всякого фильтра состоит в том, что пропустить колебания одних частот и задержать колебания других частот; иначе говоря, фильтр видоизменяет спектр воздействия. Поэтому действие и свойства фильтра естественно рассматривать с помощью частотных характеристик.