Примеры решения задач по функциям
Задача 1. Пусть 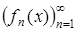 – последовательность измеримых на X функций. Тогда
– последовательность измеримых на X функций. Тогда 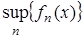 ,
, 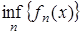 измеримы на X.
измеримы на X.
Решение. Обозначим через h(x) = 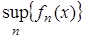 . Измеримость h(x) означает, что для " c Î R измеримы множества
. Измеримость h(x) означает, что для " c Î R измеримы множества 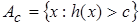 . Покажем, что
. Покажем, что 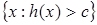 =
= 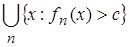 , что и будет означать измеримость h. Пусть
, что и будет означать измеримость h. Пусть 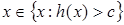 , т.е. h(x)>c. Тогда h(x)>c+e при достаточно малом e > 0. По определению точной верхней границы найдётся такой номер n0, что
, т.е. h(x)>c. Тогда h(x)>c+e при достаточно малом e > 0. По определению точной верхней границы найдётся такой номер n0, что 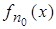 >h(x)–e. Отсюда
>h(x)–e. Отсюда 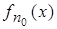 >(c+e)-e=с и потому
>(c+e)-e=с и потому 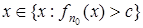 , а тем более,
, а тем более, 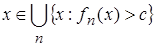 .
.
С другой стороны, пусть 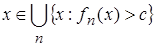 . Это значит, что найдётся такой номер n0, что
. Это значит, что найдётся такой номер n0, что 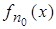 > c. Но тогда h (x) ³
> c. Но тогда h (x) ³ 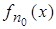 > c, т.е.
> c, т.е. 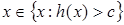 . Равенство доказано. Аналогично доказывается измеримость
. Равенство доказано. Аналогично доказывается измеримость 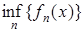 .
.
Задача 2. Определим функцию f(x) на [0,1] следующим образом. Если x = 0,n1n2… – десятичная запись числа x, то 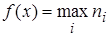 .
.
Решение. Рассмотрим множество чисел отрезка [0,1], в десятичной записи которых присутствует цифра 9. Мера данного множества равна 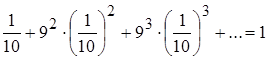 . Следовательно, функция f(x) равна 9 почти всюду. Функция f(x) измерима как постоянная функция.
. Следовательно, функция f(x) равна 9 почти всюду. Функция f(x) измерима как постоянная функция.
Задача 3. Доказать, что функция f измерима тогда и только тогда, когда измерима функция sin f.
Решение. Обозначим через g(x) = sin x, тогда при измеримости функции f имеем h(x) = g(f(x)) = sin f – композиция непрерывной и измеримой и поэтому sin f будет измеримой. С другой стороны, пусть измерима функция h(x) = sin f(x), покажем, что измерима функция f(x). Измеримость sin f означает, что для "с Î R измеримо множество {f(x):sinf(x)>c} = 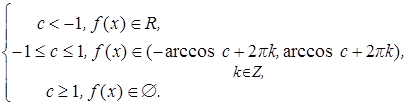
Таким образом, измеримыми являются пустое множество, числовая прямая и для "c Î R множество 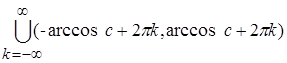 , arccos c Î[0,p].
, arccos c Î[0,p].
Задача 4. Доказать, что функция y = f(x), x Î R измерима на R, если 1) f(x) = sin[x]; 2) f(x)= 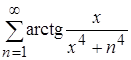 .
.
Решение. 1) Функция f(x) принимает счётное число значений sink, kÎZ. А именно, 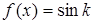 , если x Î Ak = [k, k+1[ и
, если x Î Ak = [k, k+1[ и 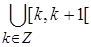 =R. Так как промежутки Ak являются измеримыми, то f(x) является простой функцией и, следовательно, измеримой.
=R. Так как промежутки Ak являются измеримыми, то f(x) является простой функцией и, следовательно, измеримой.
2) Члены рассматриваемого ряда являются непрерывными функциями и поэтому измеримы. Если x³ 0, то эквивалентность 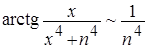 при n®¥ позволяет сделать вывод о равномерной сходимости этого функционального ряда для x ³ 0. Аналогично, если x>0, то
при n®¥ позволяет сделать вывод о равномерной сходимости этого функционального ряда для x ³ 0. Аналогично, если x>0, то 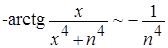 при n®¥, и поэтому для x>0 ряд
при n®¥, и поэтому для x>0 ряд 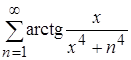 сходится равномерно. Тогда его сумма является непрерывной, а значит, измеримой функцией.
сходится равномерно. Тогда его сумма является непрерывной, а значит, измеримой функцией.
Задача 5. Доказать, что функция z = f(x, y), (x, y) Î R2 является измеримой на R2, если f(x,y)= 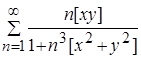 .
.
Решение. Поскольку функции z=[xy] и z=[x2+y2] простые, то они измеримы на плоскости. Измеримой для каждого номера n является функция 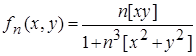 . Из сходимости функционального ряда (что устанавливается с помощью признака сравнения) следует измеримость на R2 функции f(x,y).
. Из сходимости функционального ряда (что устанавливается с помощью признака сравнения) следует измеримость на R2 функции f(x,y).
Задача 6. Для функции f построить последовательность простых измеримых функций, равномерно сходящуюся к f, если 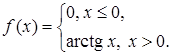
Решение. Исходя из теоремы, для измеримой конечной на множестве A функции f(x) последовательность 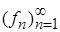 простых измеримых функций строится так: для каждого целого k
простых измеримых функций строится так: для каждого целого k 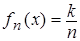 на множестве
на множестве 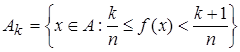 . Поэтому для x £ 0 полагаем fn(x)=0, а на множествах {x > 0 :
. Поэтому для x £ 0 полагаем fn(x)=0, а на множествах {x > 0 : 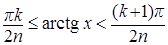 } = {x>0 :
} = {x>0 : 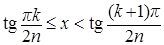 }, k = 0,1,…,n –1 полагаем
}, k = 0,1,…,n –1 полагаем 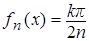 .
.
Задача 7. Доказать, что при n®¥ последовательность fn(x)=sinnpx+cosnpx сходится к нулю почти всюду на R относительно меры Лебега.
Решение. При тех xÎR, для которых |sin px|px|<1, имеем 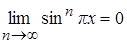 ,
, 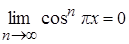 . Если же xÎR таково, что sin px = ±1 (или cos px = ±1), то предел функции sinnpx (соответственно cosnpx) равен единице или не существует. Таким образом, рассмотрим множество A0={xÎR: sin px=±1 или cos px = ±1} = {k : kÎZ}Ç{1/2+k : kÎZ}. Множество A0 – счётное (как объединение двух счётных множество) и поэтому m(A0)=0. Тогда для каждой точки xÎR\A0
. Если же xÎR таково, что sin px = ±1 (или cos px = ±1), то предел функции sinnpx (соответственно cosnpx) равен единице или не существует. Таким образом, рассмотрим множество A0={xÎR: sin px=±1 или cos px = ±1} = {k : kÎZ}Ç{1/2+k : kÎZ}. Множество A0 – счётное (как объединение двух счётных множество) и поэтому m(A0)=0. Тогда для каждой точки xÎR\A0 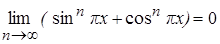 , и, следовательно, почти всюду последовательность fn(x) сходится к f(x)=0.
, и, следовательно, почти всюду последовательность fn(x) сходится к f(x)=0.
Задача 8. Для последовательности fn(x)=xn, xÎ[0,1] указать множество, на котором fn(x) сходится равномерно, причём мера множества, на котором нет сходимости, может быть сделана сколь угодно малой.
Решение. Рассмотрим произвольное d > 0. Если d ³1, то в качестве Xd возьмём, например, отрезок [0, 1/2]. Тогда m(Ad) = =1/2>m(X)–d = 1–d, где X=[0,1]. 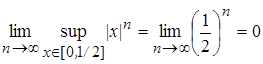 , т.е. на [0,1/2] последовательность
, т.е. на [0,1/2] последовательность 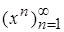 равномерно сходится к функции f(x)=0. Если же d<1, то положим Xd = [0,1-d/2], тогда m(Xd)=1-d/2>m(X)-d=1-d, т.е. m(X\Xd) =
равномерно сходится к функции f(x)=0. Если же d<1, то положим Xd = [0,1-d/2], тогда m(Xd)=1-d/2>m(X)-d=1-d, т.е. m(X\Xd) = 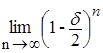 = 0.
= 0.
Задача 9. Исследовать на сходимость по мере к функции f на измеримом множестве A следующие последовательности:
1) fn(x)=xn, xÎ[0,1],
2) fn(x)=cosnx, xÎR.
Решение. 1) Рассмотрим для " d > 0 измеримое множество {xÎ[0,1] : xn ³ d} = [ 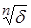 ,1]. Отметим, что когда d > 1, то множество пусто. Тогда
,1]. Отметим, что когда d > 1, то множество пусто. Тогда 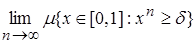 =
= 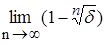 = 0 и поэтому
= 0 и поэтому 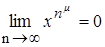 на [0,1]. С другой стороны, xn ® 0 почти всюду (см. пример), тогда
на [0,1]. С другой стороны, xn ® 0 почти всюду (см. пример), тогда 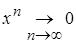 по мере.
по мере.
2) Пусть d £ 1, тогда 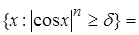
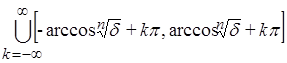 . Значит m {x Î R :
. Значит m {x Î R : 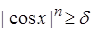 } =
} = 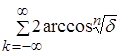 = +¥. Поэтому заданная последовательность не сходится по мере.
= +¥. Поэтому заданная последовательность не сходится по мере.
Задание 1. Пусть X = [-1,1[, на X задана мера Лебега. Выяснить, является ли функция f: 1)измеримой; 2)ограниченной; 3)простой. Найти все её точки непрерывности и точки разрыва. Построить эквивалентную функцию с минимальным множеством точек разрыва.
1.1. 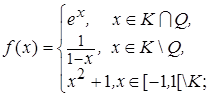
1.2. 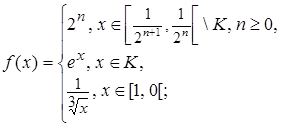
1.3. 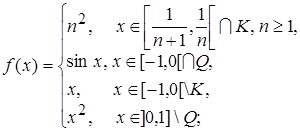
1.4. 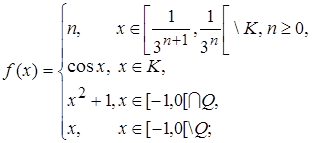
1.5. 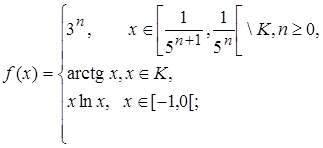
1.6. 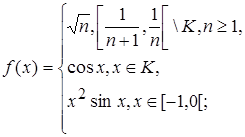
1.7. 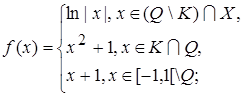
1.8. 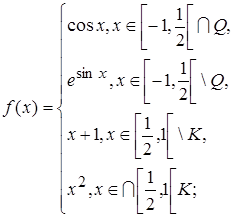
1.9. 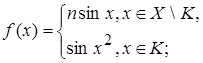
1.10. 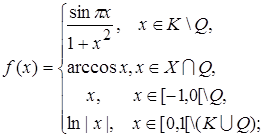
1.11. 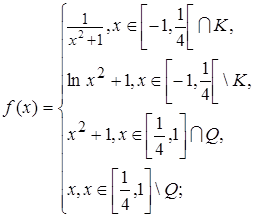
1.12. 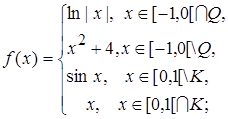
1.13. 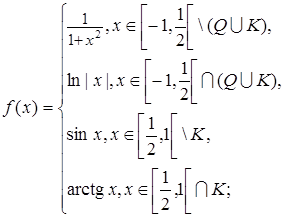
1.14. 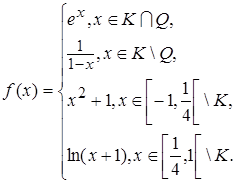
Задание 2. Доказать, что функция y = f(x), xÎRn измерима на Rn.
2.1. 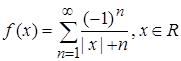
2.2. 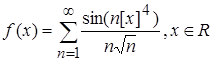
2.3. 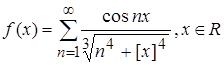
2.4. 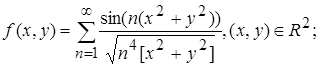
2.5. 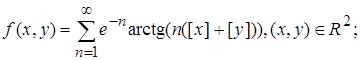
2.6. 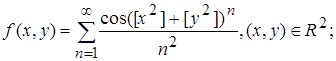
2.7. 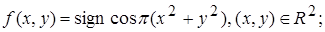
2.8. 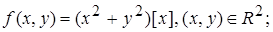
2.9. 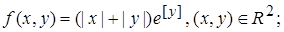
2.10. 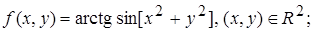
2.11. 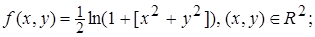
2.12. 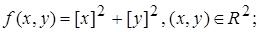
2.13. 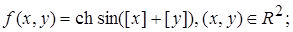
2.14. 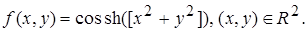
Задание 3. Для заданной на отрезке [0,1] функции f построить последовательность fn простых функций, равномерно сходящуюся к f.
3.1. 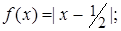
3.2. 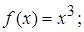
3.3. 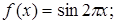
3.4. 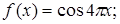
3.5. 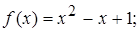
3.6. 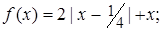
3.7. 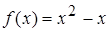
3.8. 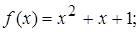
3.9. 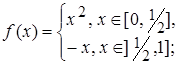
3.10. 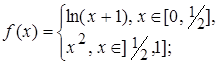
3.11. 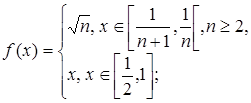
3.12. 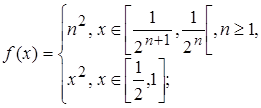
3.13. 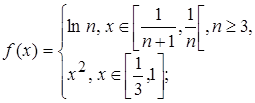
3.14. 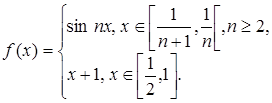
Задание 4. Исследовать на сходимость следующие последовательности:
4.1. 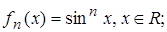
4.2. 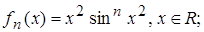
4.3. 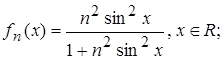
4.4. 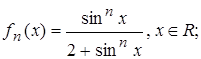
4.5. 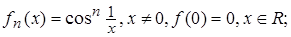
4.6. 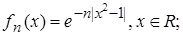
4.7. 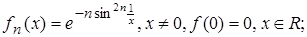
4.8. 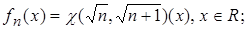
4.9. 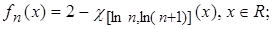
4.10. 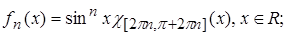
4.11. 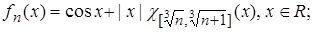
4.12. 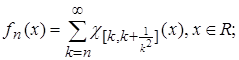
4.13. 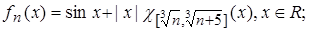
4.14. 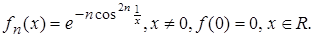
Дата добавления: 2021-07-22; просмотров: 702;











