Сходимость по мере.

Точечная сходимость.

Последовательность f_n сходится к функции f поточечно, если для всех xÎX f_n(x)®f(x) при n®¥.

Равномерная сходимость.

Последовательность функций f_n сходится к f равномерно, если для любого e > 0 существует n_e такой, что при n>n_e |f_n(x) –f(x)| < e для всех xÎX.

Сходимость почти всюду.

Последовательность f_n сходится к f, если f_n(x)®f(x) при n®¥ для всех xÎX за исключением множества меры нуль.

Сходимость по мере.

Говорят, что последовательность конечных измеримых функций f_n сходится по мере к измеримой функции f, если для всякого числа d > 0

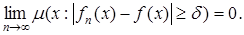
Очевидно, что из равномерной сходимости следует сходимость точечная, а из точечной – сходимость почти всюду.

Теорема 4. Пусть последовательность f_n(x) измеримых функций для всех xÎX сходится к функции f. Тогда и функция f измерима.

Следствие 1. Если 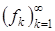, f_k(x)ÎS(X) сходится к f равномерно, то f(x)ÎS(X).

Следствие 2. Если 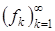, f_k(x)ÎS(X) сходится к f почти всюду, то f(x)ÎS(X).

Следствие 3. Существует разрывная на отрезке [a;b] функция, которая не является пределом почти всюду сходящейся последовательности непрерывных функций.

В качестве такой функции можно взять неизмеримую функцию.

Теорема 5 (Лебега). Пусть последовательность 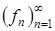конечных измеримых функций сходится к измеримой функции f почти всюду. Тогда она сходится и по мере.

Теорема 6 (Рисса). Пусть последовательность 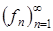конечных измеримых функций сходится к измеримой функции f по мере. Тогда из этой последовательности можно выделить подпоследовательность 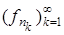, сходящуюся почти всюду.

Пусть задано пространство (X, S, m) с конечной мерой. Говорят, что некоторое свойство выполнено почти всюду, если оно выполнено на X/A, а m(A)=0.

Будем рассматривать числовые функции, которые почти всюду конечны.

Две функции f и g называются эквивалентными, если они совпадают почти всюду, т.е. m{x: f¹g}=0.

Теорема 7. Пусть f Î S(X) и f ~ g, тогда gÎ S(X).

Теорема 8 (Егорова). Пусть X – пространство с конечной мерой и последовательность 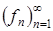измеримых функций сходится почти всюду на X к измеримой функции f. Тогда для любого d >0 найдётся такое измеримое множество X_d ÌX, что:

1) m(X\X_d)<d;

2) на X_d последовательность 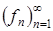сходится к f равномерно.

Теорема 9 (Лузина). Пусть X Ì R – измеримое по Лебегу множество конечной меры и пусть f : X® R измерима и почти всюду конечна. Тогда для всех e > 0 существует F_e Ì X – замкнутое множество, что функция f на F_e непрерывна и m (X\F_e) <e.