Основные параметры весовых функций
В таблице 9.3 приведены используемые при синтезе ЦФ параметры весовых функций прямоугольной, треугольной, Ханна, Хэмминга Блэкмана. Таблица содержит значения ширины главного лепестка 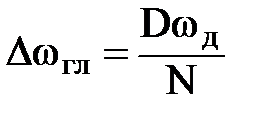 , (где D – так называемый D-фактор), и максимального уровня боковых лепестков абmax.
, (где D – так называемый D-фактор), и максимального уровня боковых лепестков абmax.
Таблица 9.3
| № | Тип | Δωгл | абmax, дБ |
| Прямоугольная | 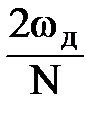
| -13.6 | |
| Треугольная | 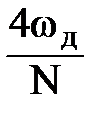
| -27 | |
| Хана | 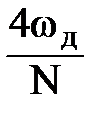
| -31 | |
| Хэмминга | 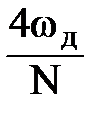
| -41 | |
| Блэкмана | 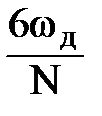
| -57 |
Руководствуясь данными табл. 9.3, можно по требуемому затуханию частотной характеристики в полосе задерживания аз сделать выбор типа весовой функции.
В этом разделе приводятся характеристики некоторых весовых функций используемых при расчете.
Простейшая весовая функция – прямоугольная – имеет минимальную ширину главного лепестка и максимальный уровень боковых лепестков. Частотная характеристика ее (Рис. 9.31,а) определяется выражением:
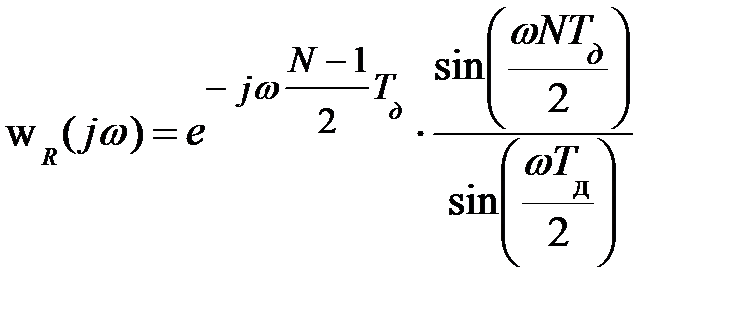
Боковые лепестки весовой функции имеют ширину 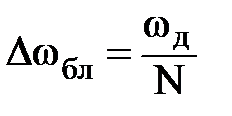 . Треугольная весовая функция (или окно Бартлетта) определяется выражением:
. Треугольная весовая функция (или окно Бартлетта) определяется выражением:
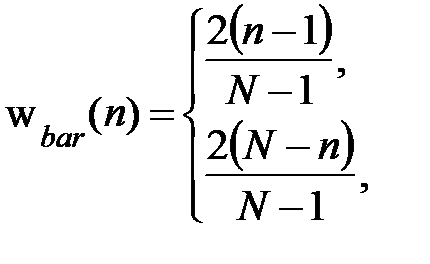
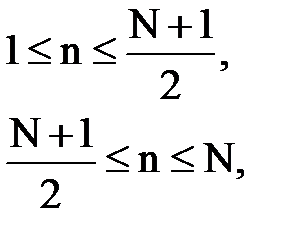 для нечетного N,
для нечетного N,

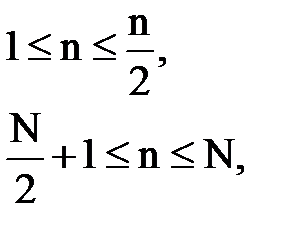 для четного N.
для четного N.
У нее вдвое большая ширина главного лепестка при достаточно большом уровне боковых лепестков.
Частотная характеристика треугольной весовой функции равна квадрату частотной характеристики прямоугольной весовой функции половинной длины:
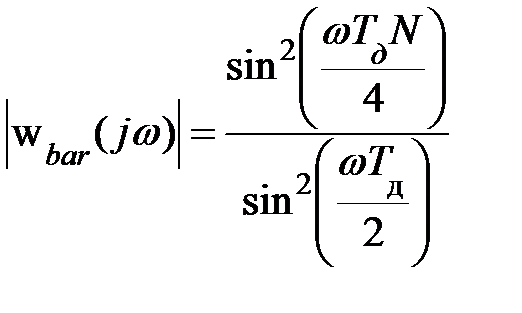
Боковые лепестки ее имеют ширину 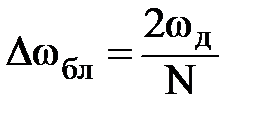 или
или 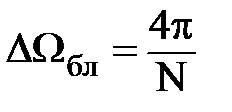 .
.
Обобщенная весовая функция Хэмминга описывается выражением:
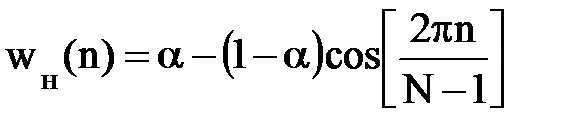
При α = 0.5 она соответствует весовой функции Хана, при α = 0.54 – весовой функции Хэмминга (рис. 9.31,б).
а) б) в)
Рис. 9.31 Частотная характеристика прямоугольной весовой функции (а), весовая функция Хемминга (б) и ещё частотная характеристика (в)
Уровень боковых лепестков весовой функции Хэмминга оказывается приемлемым для многих приложений НФ.
Частотную характеристику весовой функции Хэмминга (рис. 9.31,в) можно представить суммой трех частотных характеристик прямоугольных весовых функций с центральными частотами ωо = 0 и 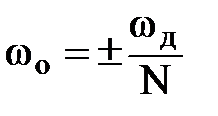 :
:
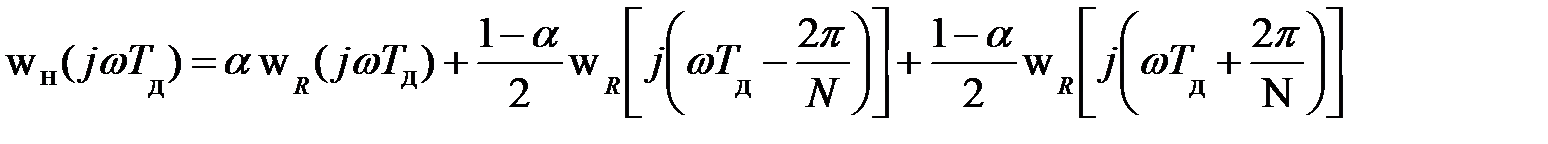
Боковые лепестки частотной характеристики имеют ширину 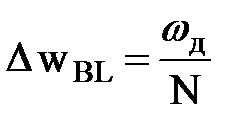 . Площадь под боковыми лепестками составляет 0.04 % от площади квадрата частотной характеристики весовой функции.
. Площадь под боковыми лепестками составляет 0.04 % от площади квадрата частотной характеристики весовой функции.
Весовая функция Блэкмана имеет вид:
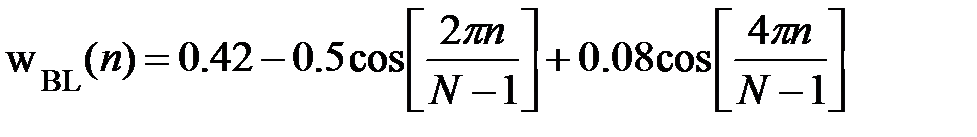
По сравнению с весовой функцией Хэмминга у нее более широкий главный лепесток (в 1.5 раза) при очень малом уровне боковых лепестков.
Частотная характеристика весовой функции Блэкмана по сравнению с весовой функции Хэмминга содержит два дополнительных слагаемых 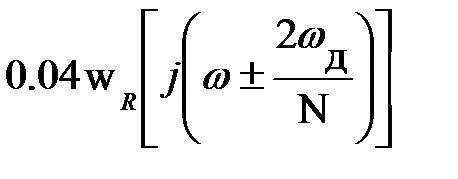 . Ширина боковых лепестков этой весовой функции
. Ширина боковых лепестков этой весовой функции 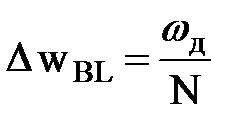 .
.
При синтезе НФ используются также весовые функции Ланцоша, Дольфа – Чебышева, Карре, Лапласа – Гаусса и др., среди которых особое значение имеет класс весовых окон Кайзера.
В отличие от других весовых функций, характеризующихся постоянными значениями уровня боковых лепестков аблmax. и фактором D, у весовых функций Кайзера эти параметры могут широко варьироваться с помощью коэффициента β, входящего в математическое выражение этой функции:
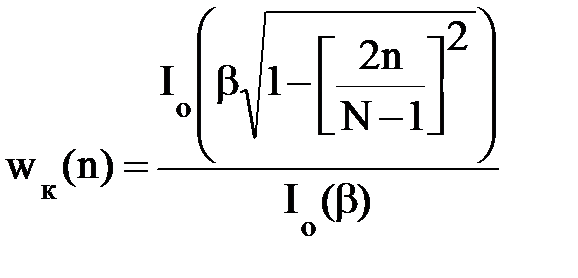 ,
,
где Io(х) – функция Бесселя нулевого порядка.
Благодаря этому обеспечивается наилучшее для данного метода синтеза качество аппроксимации заданной частотной характеристики или наименьший порядок фильтра при заданном качестве аппроксимации.
Кайзером путем численного интегрирования свертки получены эмпирические формулы, которые позволяют непосредственно по заданному затуханию аз частотной характеристики Hid(jω) рассчитать значения D – фактора и коэффициенты β [11]:
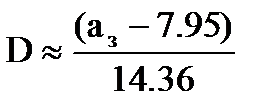 при аз > 21 дБ;
при аз > 21 дБ;
D = 0.9222 при аз < 21 дБ;
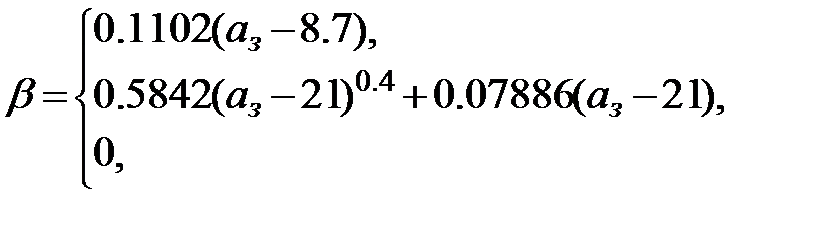
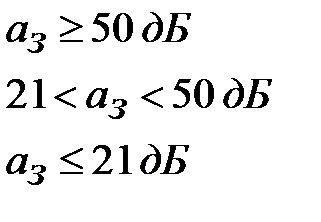
По вычисленному или взятому из таблицы 9.4 значению D определяется необходимый порядок фильтра 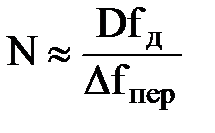 , который округляется затем до ближайшего целого большего, чаще всего нечетного числа.
, который округляется затем до ближайшего целого большего, чаще всего нечетного числа.
Как и для других весовых функций, в случае аппроксимации идеальных фильтров типа ППФ, ПЗФ, МПФ затухание частотной характеристики в полосе задерживания может быть меньше его расчетного значения, но не более чем на 6 дБ. В таблице 9.4 приведены расчетные коэффициентов β и D для различных значений рабочего затухания аз.
Таблица 9.4
| аз, дБ | β | D | аз, дБ | β | D |
| 1.333 | 1.187 | 6.204 | 3.973 | ||
| 2.117 | 1.536 | 6.755 | 4.321 | ||
| 2.783 | 1.884 | 7.306 | 4.669 | ||
| 3.395 | 2.232 | 7.857 | 5.017 | ||
| 3.975 | 2.580 | 8.408 | 5.366 | ||
| 4.551 | 2.928 | 8.959 | 5.714 | ||
| 5.102 | 3.261 | 9.501 | 6.062 | ||
| 5.653 | 3.625 | 10.061 | 6.410 |
Дата добавления: 2017-05-02; просмотров: 4318;











