Модуль действительного числа
· Определение модуля действительного числа:
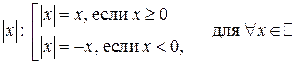
· Геометрический смысл модуля действительного числа: 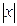 — это расстояние от точки x до точки 0 на координатной прямой, (рис. 14). — это расстояние от точки x до точки 0 на координатной прямой, (рис. 14).
| |
· Геометрический смысл модуля разности двух действительных чисел:
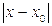 геометрически определяет расстояние между точками x и x0 на координатной прямой, (рис. 15). геометрически определяет расстояние между точками x и x0 на координатной прямой, (рис. 15).
| |
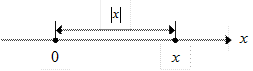 Рис. 14
Рис. 14
| 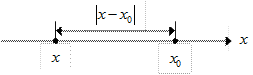 Рис. 15
Рис. 15
|
· Основные свойства модуля действительного числа:
1) 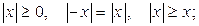
2) 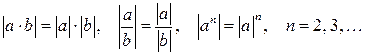 ;
;
3) 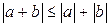 — неравенство треугольника;
— неравенство треугольника;
4) 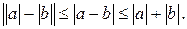
2.3. Стандартные подмножества множества действительных чисел 
Стандартными подмножествами множества  называются следующие
называются следующие
множества:
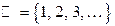 — множество натуральных чисел, то есть множество чисел, которые получаются в результате счёта целых предметов;
— множество натуральных чисел, то есть множество чисел, которые получаются в результате счёта целых предметов;
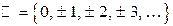 — множество целых чисел;
— множество целых чисел;
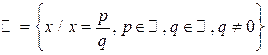 — множество рациональных чисел;
— множество рациональных чисел;
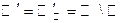 — множество иррациональных чисел.
— множество иррациональных чисел.
 — это универсальное числовое множество для всех других числовых множеств, элементами которых являются действительные числа.
— это универсальное числовое множество для всех других числовых множеств, элементами которых являются действительные числа.
Включения стандартных подмножеств множества  показано на рис.16
показано на рис.16
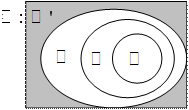 Рис. 16
Рис. 16
| 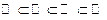 , , 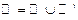
|
На множестве натуральных чисел 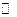 вводятся следующие понятия:
вводятся следующие понятия:
· простые числа — это числа, которые делятся только на себя и на 1;
· составные числа — это числа, которые делятся не только на себя и на 1;
· число 1 не относится ни к простым, ни к составным числам;
· взаимно простые числа — это числа, не имеющие общих делителей, отличных от 1;
· наименьшее общее кратное (НОК) нескольких чисел — это наименьшее натуральное число, которое делится на все эти числа;
· наибольший общий делитель (НОД) нескольких чисел — это наибольшее натуральное число, на которое делятся все эти числа.
О записи действительных чисел
Каждое действительное число x может быть записано бесконечной десятичной дробью.
Например, 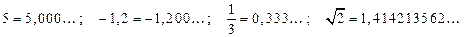 .
.
Если число x является рациональным, т.е. 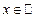 , то оно записывается конечной или бесконечной периодической десятичной дробью.
, то оно записывается конечной или бесконечной периодической десятичной дробью.
Например, 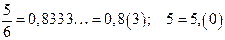 ;
; 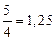 ;
; 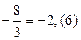 .
.
Если число x является иррациональным, т.е. 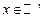 , то оно записывается бесконечной непериодической десятичной дробью.
, то оно записывается бесконечной непериодической десятичной дробью.
Например, 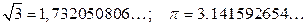 .
.
Если в арифметическом выражении участвуют только рациональные числа, то можно найти точное значение такого выражения, выполнив все арифметические операции без погрешностей. Если же в арифметическое выражение входит хотя бы одно иррациональное число, то значение такого выражения находится приближённо.
Например, 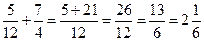 ;
; 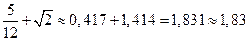 .
.
2.4. Примеры работы на множестве 
Пример 1 (геометрический смысл модуля)
Построить на числовой прямой и записать промежутками следующие множества, используя геометрический смысл модуля разности двух действительных чисел:
a) 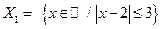 ; б)
; б) 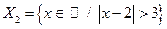 ; в)
; в) 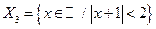 .
.
Решение
| а) | 
| 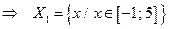 ; ;
|
пояснения:
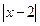 — это расстояние от точек х до точки 2;
— это расстояние от точек х до точки 2;
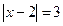 — это множество точек x, отстоящих от точки 2 на расстоянии, равном 3; состоит из точек
— это множество точек x, отстоящих от точки 2 на расстоянии, равном 3; состоит из точек 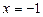 и
и 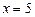 ;
;
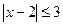 — это множество точек x, отстоящих от точки 2 на расстоянии, меньшем
— это множество точек x, отстоящих от точки 2 на расстоянии, меньшем
либо равном 3; оно включает в себя все точки, принадлежащие промежутку 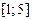 .
.
| б) | 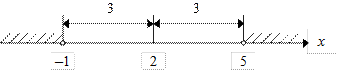
| 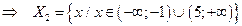 ; ;
|
пояснение:
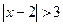 — это множество точек x, отстоящих от точки 2 на расстоянии, большем, чем 3.
— это множество точек x, отстоящих от точки 2 на расстоянии, большем, чем 3.
| в) | 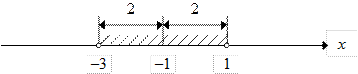
| 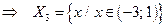 ; ;
|
пояснения:
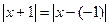 — это расстояние от точек x до точки –1;
— это расстояние от точек x до точки –1;
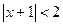 — это множество точек x, отстоящих от точки –1 на расстоянии,
— это множество точек x, отстоящих от точки –1 на расстоянии,
меньшем 2.
Пример 2 (стандартные подмножества множества  )
)
Дано 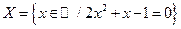 . Найти
. Найти 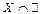 ,
, 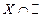 ,
, 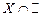 .
.
Решение
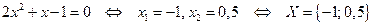
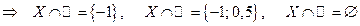 .
.
Дата добавления: 2021-07-22; просмотров: 683;











