Способы задания графов

Уже отмечалось, что произвольный граф можно задать совокупностью двух множеств: X – множества вершин и U – множества ребер (дуг) графа или множества X и отображения Г множества Х в Х.

Другой удобной формой описания графов является представление их с помощью матриц, методика формального получения которых хорошо разработана.

Матрица смежности.Из ранее сказанного известно, что две вершины x_i и x_jÎX графа G(X, U) называются смежными, если они являются граничными вершинами ребра u_rÎU

Отношение смежности на множестве вершин графа можно определить, представив каждое ребро как пару смежных вершин, т.е. u_r=(x_i, x_j), r=1, 2, ..., k.

Для неориентированных графов такие пары неупорядочены, так что

u_k=(x_i, x_j)=(x_j, x_i), а для орграфов - упорядочены, причем, x_i, и x_j означают, соответственно, начальную и конечную вершины дуги u_r. Петля при вершине x_j в обоих случаях представляется неупорядоченной парой (x_j, x_j).

Множество вершин X вместе с определенным на нем отношением смежности полностью определяет граф.

Граф можно представить матрицей смежности A=||a_ij||_n´n, где n число вершин графа.

Строки и столбцы матрицы соответствуют вершинам графа, а ее a_ij элемент равен числу кратных ребер, связывающих вершины x_i, и x_j (или направленных от вершины x_i, квершине x_j для орграфов).

На рис. 3.14 представлены граф и его матрица смежности.

х2

х3

х4

х1

х5

Рисунок 3.14. граф G(X, U) и его матрица смежности

Матрица смежности неориентированного графа всегда симметрична, а орграфа - в общем случае несимметрична. Неориентированным ребрам соответствуют пары ненулевых элементов, симметричных относительно главной диагонали матрицы, а петлям - ненулевые элементы главной диагонали.

В столбцах и строках, соответствующих изолированным вершинам, все элементы равны нулю. Элементы матрицы простого графа равны 0 или 1, причем, элементы главной диагонали равны 0.

Правильность составления матрицы легко проверить: для неориентированного графа сумма элементов в каждом i -том столбце или строке соответствует степени вершины r(x_i).

При решении целого класса задач проектирования электронных устройств, приходится оперировать матрицами, которые строятся аналогично матрицам смежности, но значения их элементов определяются весом, связанным с ребром (дугой) графа.

Матрица весов. Это квадратная матрица C=||c_ij||_n´n, элемент которой

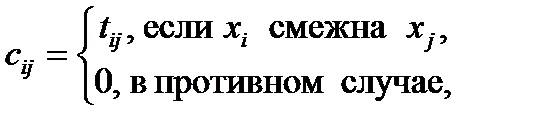где t_ij - вес связи (x_j, x_j).

Применение матриц весов позволяет учитывать различные требования к сокращению длины тех или иных электрических соединений в конструкциях ЭВМ, условия тепловой и электромагнитной совместимости отдельных элементов схемы и другие.

Матрица инцидентности.В то время как смежность представляет собой отношение между однородными объектами (вершинами), инцидентность - это отношение между разнородными объектами (вершинами и ребрами).

Рассматривая инцидентность вершин и ребер графа, можно представить его матрицей инцидентности B=||b_ij|| _n´k, строки которой соответствуют вершинам, а столбцы – ребрам,

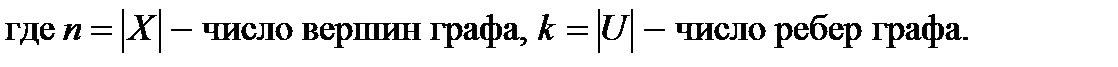
Для неографа:

Для орграфа:

На рис. 3.15 представлены граф G(X, U) и его матрица инцидентности.

u7

u6

u5

u4

u3

u1

u2

х2

х3

х4

х1

х5

х2

х3

х4

х1

х5

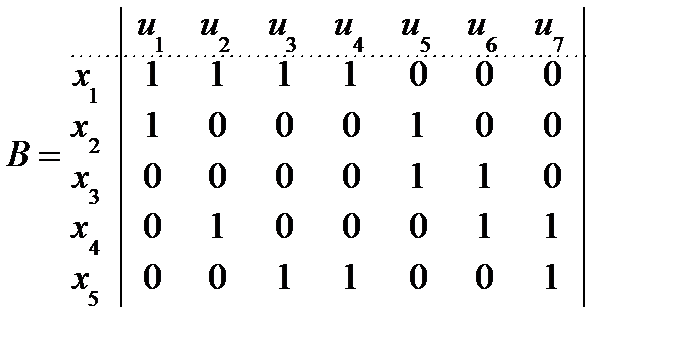
Рисунок 3.15. Граф G(X, U) и его матрица инцидентности

Количество единиц в строке равно степени соответствующей вершины (для орграфа количество положительных единиц определяет положительную степень, а количество отрицательных единиц - отрицательную степень).

Граф однозначно задается матрицами смежности и инцидентности. В свою очередь, каждая из этих матриц полностью определяет граф.

Существуют простые приемы перехода от одной матрицы к другой.

Матрица длин.Это квадратная матрица D=||d_ij||_n´n, элемент которой

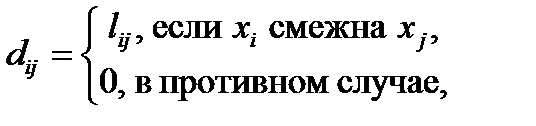где l_ij – длина ребра (x_j,, x_j).

В САПР используют различные метрики.

Если проводники разрешается проводить под любым углом (например, проводной монтаж), то используют евклидову метрику

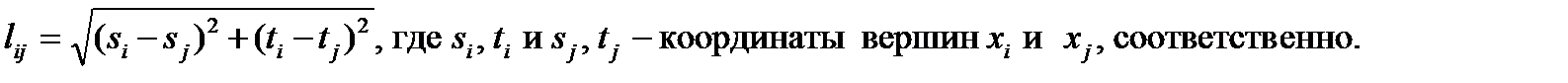
Если проводники разрешается проводить только параллельно осям (ортогонально), то пользуются ортогональной метрикой (так называемое манхэттенское расстояние)

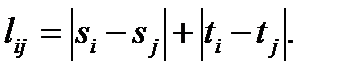
При проектировании печатного монтажа для уменьшения числа межслойных переходов стараются вертикальные и горизонтальные проводники распределять по разным слоям. В этом случае расстояние между двумя точками представляется в виде степенной функции:

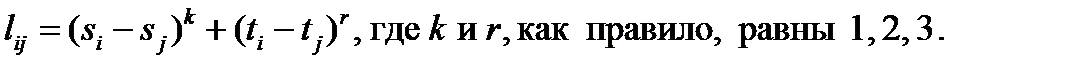
Матрицу длин используют при решении задач оптимизации размещения конструктивных элементов на плате, когда одним из критериев качества является суммарная длина соединений.