Алгоритм Флойда – Уоршелла
Алгоритм Дейкстры
Алгоритм голландского ученого Эдсгера Дейкстры находит все кратчайшие пути из одной изначально заданной вершины графа до всех остальных. С его помощью, при наличии всей необходимой информации, можно, например, узнать какую последовательность дорог лучше использовать, чтобы добраться из одного города до каждого из многих других, или в какие страны выгодней экспортировать нефть и тому подобное. Минусом данного метода является невозможность обработки графов, в которых имеются ребра с отрицательным весом, т. е. если, например, некоторая система предусматривает убыточные для Вашей фирмы маршруты, то для работы с ней следует воспользоваться отличным от алгоритма Дейкстры методом.
Для программной реализации алгоритма понадобиться два массива: логический visited – для хранения информации о посещенных вершинах и численный distance, в который будут заноситься найденные кратчайшие пути. Итак, имеется граф G=(V, E). Каждая из вершин входящих во множество V, изначально отмечена как не посещенная, т. е. элементам массива visited присвоено значение false. Поскольку самые выгодные пути только предстоит найти, в каждый элемент вектора distance записывается такое число, которое заведомо больше любого потенциального пути (обычно это число называют бесконечностью, но в программе используют, например максимальное значение конкретного типа данных). В качестве исходного пункта выбирается вершина s и ей приписывается нулевой путь: distance[s]=0, т. к. нет ребра из s в s (метод не предусматривает петель). Далее, находятся все соседние вершины (в которые есть ребро из s) [пусть таковыми будут t и u] и поочередно исследуются, а именно вычисляется стоимость маршрута из s поочередно в каждую из них:
· distance[t]=distance[s]+весинцидентного s и t ребра;
· distance[u]=distance[s]+ весинцидентного s и u ребра.
Но вполне вероятно, что в ту или иную вершину из s существует несколько путей, поэтому цену пути в такую вершину в массиве distance придется пересматривать, тогда наибольшее (неоптимальное) значение игнорируется, а наименьшее ставиться в соответствие вершине.
После обработки смежных с s вершин она помечается как посещенная: visited[s]=true, и активной становится та вершина, путь из s в которую минимален. Допустим, путь из s в u короче, чем из s в t, следовательно, вершина u становиться активной и выше описанным образом исследуются ее соседи, за исключением вершины s. Далее, u помечается как пройденная: visited[u]=true, активной становится вершина t, и вся процедура повторяется для нее. Алгоритм Дейкстры продолжается до тех пор, пока все доступные из s вершины не будут исследованы.
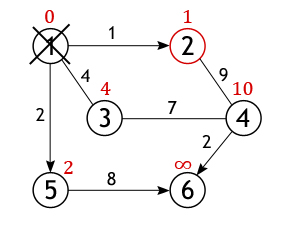
Теперь на конкретном графе проследим работу алгоритма, найдем все кратчайшие пути между истоковой и всеми остальными вершинами. Размер (количество ребер) изображенного ниже графа равен 7 (|E|=7), а порядок (количество вершин) – 6 (|V|=6). Это взвешенный граф, каждому из его ребер поставлено в соответствие некоторое числовое значение, поэтому ценность маршрута необязательно определяется числом ребер, лежащих между парой вершин.
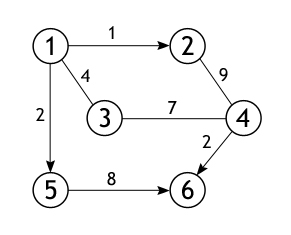
Из всех вершин входящих во множество V выберем одну, ту, от которой необходимо найти кратчайшие пути до остальных доступных вершин. Пусть таковой будет вершина 1. Длина пути до всех вершин, кроме первой, изначально равна бесконечности, а до нее – 0, т. к. граф не имеет петель.
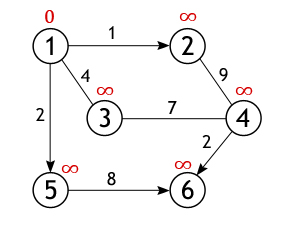
У вершины 1 ровно 3 соседа (вершины 2, 3, 5), и чтобы вычислить длину пути до них нужно сложить вес дуг, лежащих между вершинами: 1 и 2, 1 и 3, 1 и 5 со значением первой вершины (с нулем):
· 2←1+0
· 3←4+0
· 5←2+0
Как уже отмечалось, получившиеся значения присваиваются вершинам, лишь в том случае если они «лучше» (меньше) тех которые значатся на настоящий момент. А так как каждое из трех чисел меньше бесконечности, они становятся новыми величинами, определяющими длину пути из вершины 1 до вершин 2, 3 и 5.
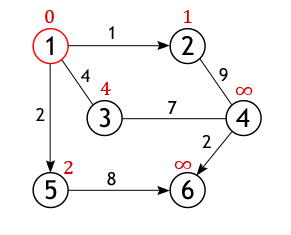
Далее, активная вершина помечается как посещенная, статус «активной» (красный круг) переходит к одной из ее соседок, а именно к вершине 2, поскольку она ближайшая к ранее активной вершине.
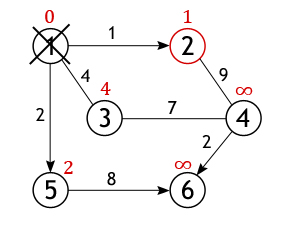
У вершины 2 всего один не рассмотренный сосед (вершина 1 помечена как посещенная), расстояние до которого из нее равно 9, но нам необходимо вычислить длину пути из истоковой вершины, для чего нужно сложить величину приписанную вершине 2 с весом дуги из нее в вершину 4:
· 4←1+9
Условие «краткости» (10<∞) выполняется, следовательно, вершина 4 получает новое значение длины пути.
Вершина 2 перестает быть активной, также как и вершина 1 удаляется из списка не посещённых. Теперь тем же способом исследуются соседи вершины 5, и вычисляется расстояние до них. 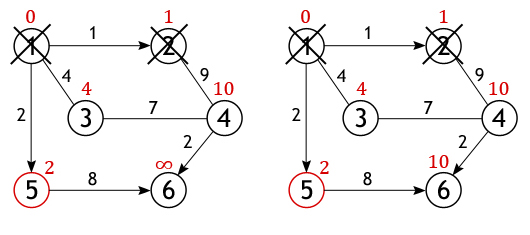
Когда дело доходит до осмотра соседей вершины 3, то тут важно не ошибиться, т. к. вершина 4 уже была исследована и расстояние одного из возможных путей из истока до нее вычислено. Если двигаться в нее через вершину 3, то путь составит 4+7=11, а 11>10, поэтому новое значение игнорируется, старое остается.
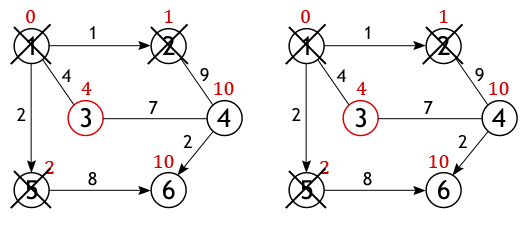 Аналогичная ситуация с вершиной 6. Значение самого близкого пути до нее из вершины 1 равно 10, а оно получается только в том случае, если идти через вершину 5.
Аналогичная ситуация с вершиной 6. Значение самого близкого пути до нее из вершины 1 равно 10, а оно получается только в том случае, если идти через вершину 5. 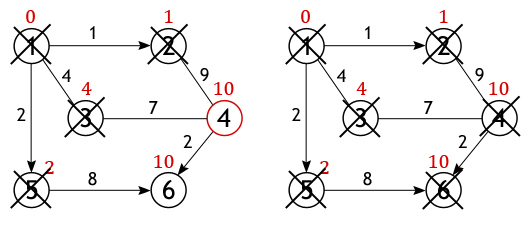 Когда все вершины графа, либо все те, что доступны из истока, будут помечены как посещенные, тогда работа алгоритма Дейкстры завершится, и все найденные пути будут кратчайшими. Так, например, будет выглядеть список самых оптимальных расстояний лежащих между вершиной 1 и всеми остальными вершинами, рассматриваемого графа:
Когда все вершины графа, либо все те, что доступны из истока, будут помечены как посещенные, тогда работа алгоритма Дейкстры завершится, и все найденные пути будут кратчайшими. Так, например, будет выглядеть список самых оптимальных расстояний лежащих между вершиной 1 и всеми остальными вершинами, рассматриваемого графа:
1→1=0
1→2=1
1→3=4
1→4=10
1→5=2
1→6=10
В программе, находящей ближайшие пути между вершинами посредством метода Дейкстры, граф будет представлен в виде не бинарной матрицы смежности. Вместо единиц в ней будут выставлены веса ребер, функция нулей останется прежней: показывать, между какими вершинами нет ребер или же они есть, но отрицательно направленны.
Код программы на C++:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 | #include "stdafx.h"#include <iostream> using namespace std; const int V=6; //алгоритм Дейкстры void Dijkstra(int GR[V][V], int st) { int distance[V], count, index, i, u, m=st+1; bool visited[V]; for (i=0; i<V; i++) { distance[i]=INT_MAX; visited[i]=false; } distance[st]=0; for (count=0; count<V-1; count++) { int min=INT_MAX; for (i=0; i<V; i++) if (!visited[i] && distance[i]<=min) { min=distance[i]; index=i; } u=index; visited[u]=true; for (i=0; i<V; i++) if (!visited[i] && GR[u][i] && distance[u]!=INT_MAX && distance[u]+GR[u][i]<distance[i]) distance[i]=distance[u]+GR[u][i]; } cout<<"Стоимость пути из начальной вершины до остальных:\t\n"; for (i=0; i<V; i++) if (distance[i]!=INT_MAX) cout<<m<<" > "<<i+1<<" = "<<distance[i]<<endl; else cout<<m<<" > "<<i+1<<" = "<<"маршрут недоступен"<<endl; } //главная функция void main() { setlocale(LC_ALL, "Rus"); int start, GR[V][V]={ {0, 1, 4, 0, 2, 0}, {0, 0, 0, 9, 0, 0}, {4, 0, 0, 7, 0, 0}, {0, 9, 7, 0, 0, 2}, {0, 0, 0, 0, 0, 8}, {0, 0, 0, 0, 0, 0}}; cout<<"Начальная вершина >> "; cin>>start; Dijkstra(GR, start-1); system("pause>>void"); } |
Алгоритм Флойда – Уоршелла
Наиболее часто используемое название, метод получил в честь двух американских исследователей Роберта Флойда и Стивена Уоршелла, одновременно открывших его в 1962 году. Реже встречаются другие варианты наименований: алгоритм Рой – Уоршелла или алгоритм Рой – Флойда. Рой – фамилия профессора, который разработал аналогичный алгоритм на 3 года раньше коллег (в 1959 г.), но это его открытие осталось безвестным. Алгоритм Флойда – Уоршелла – динамический алгоритм вычисления значений кратчайших путей для каждой из вершин графа. Метод работает на взвешенных графах, с положительными и отрицательными весами ребер, но без отрицательных циклов, являясь, таким образом, более общим в сравнении с алгоритмом Дейкстры, т. к. последний не работает с отрицательными весами ребер, и к тому же классическая его реализация подразумевает определение оптимальных расстояний от одной вершины до всех остальных.
Для реализации алгоритма Флойда – Уоршелла сформируем матрицу смежности D[][] графа G=(V, E), в котором каждая вершина пронумерована от 1 до |V|. Эта матрица имеет размер |V|´|V|, и каждому ее элементу D[i][j] присвоен вес ребра, идущего из вершины i в вершину j. По мере выполнения алгоритма, данная матрица будет перезаписываться: в каждую из ее ячеек внесется значение, определяющее оптимальную длину пути из вершины i в вершину j (отказ от выделения специального массива для этой цели сохранит память и время). Теперь, перед составлением основной части алгоритма, необходимо разобраться с содержанием матрицы кратчайших путей. Поскольку каждый ее элемент D[i][j] должен содержать наименьший из имеющихся маршрутов, то сразу можно сказать, что для единичной вершины он равен нулю, даже если она имеет петлю (отрицательные циклы не рассматриваются), следовательно, все элементы главной диагонали (D[i][i]) нужно обнулить. А чтобы нулевые недиагональные элементы (матрица смежности могла иметь нули в тех местах, где нет непосредственного ребра между вершинами i и j) сменили по возможности свое значение, определим их равными бесконечности, которая в программе может являться, например, максимально возможной длинной пути в графе, либо просто – большим числом.Ключевая часть алгоритма, состоя из трех циклов, выражения и условного оператора, записывается довольно компактно:
Для k от 1 до |V| выполнять
Для i от 1 до |V| выполнять
Для j от 1 до |V| выполнять
Если D[i][k]+D[k][j]<D[i][j] то D[i][j] ←D[i][k]+D[k][j]
Кратчайший путь из вершины i в вершину j может проходить, как только через них самих, так и через множество других вершин k∈(1, …, |V|). Оптимальным из i в j будет путь или не проходящий через k, или проходящий. Заключить о наличии второго случая, значит установить, что такой путь идет из i до k, а затем из k до j, поэтому должно заменить, значение кратчайшего пути D[i][j] суммой D[i][k]+D[k][j].Рассмотрим полный код алгоритма Флойда – Уоршелла на C++ и Паскале, а затем детально разберем последовательность выполняемых им действий.
Код программы на C++:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 | #include "stdafx.h"#include <iostream> using namespace std; const int maxV=1000; int i, j, n; int GR[maxV][maxV]; //алгоритм Флойда-Уоршелла void FU(int D[][maxV], int V) { int k; for (i=0; i<V; i++) D[i][i]=0; for (k=0; k<V; k++) for (i=0; i<V; i++) for (j=0; j<V; j++) if (D[i][k] && D[k][j] && i!=j) if (D[i][k]+D[k][j]<D[i][j] || D[i][j]==0) D[i][j]=D[i][k]+D[k][j]; for (i=0; i<V; i++) { for (j=0; j<V; j++) cout<<D[i][j]<<"\t"; cout<<endl; } } //главная функция void main() { setlocale(LC_ALL, "Rus"); cout<<"Количество вершин в графе > "; cin>>n; cout<<"Введите матрицу весов ребер:\n"; for (i=0; i<n; i++) for (j=0; j<n; j++) { cout<<"GR["<<i+1<<"]["<<j+1<<"] > "; cin>>GR[i][j]; } cout<<"Матрица кратчайших путей:"<<endl; FU(GR, n); system("pause>>void"); } |
Положим, что в качестве матрицы смежности, каждый элемент которой хранит вес некоторого ребра, была задана следующая матрица:
Количество вершин в графе, представлением которого является данная матрица, равно 3, и, причем между каждыми двумя вершинами существует ребро. Вот собственно сам этот граф:
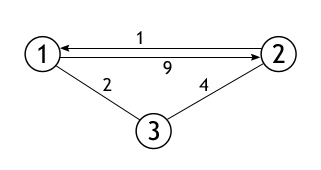 Задача алгоритма: перезаписать данную матрицу так, чтобы каждая ячейка вместо веса ребра из i в j, содержала кратчайший путь из i в j. Для примера взят совсем маленький граф, и поэтому не будет не чего удивительного, если матрица сохранит свое изначальное состояние. Но результат тестирования программы показывает замену двух значений в ней. Следующая схема поможет с анализом этого конкретного примера.
Задача алгоритма: перезаписать данную матрицу так, чтобы каждая ячейка вместо веса ребра из i в j, содержала кратчайший путь из i в j. Для примера взят совсем маленький граф, и поэтому не будет не чего удивительного, если матрица сохранит свое изначальное состояние. Но результат тестирования программы показывает замену двух значений в ней. Следующая схема поможет с анализом этого конкретного примера.

В данной таблице показаны 27 шагов выполнения основной части алгоритма. Их столько по той причине, что время выполнения метода равно O(|V|3). Наш граф имеет 3 вершины, а 33=27. Первая замена происходит на итерации, при которой k=1, i=2, а j=3. В тот момент D[2][1]=1, D[1][3]=2, D[2][3]=4. Условие истинно, т. е. D[1][3]+D[3][2]=3, а 3<4, следовательно, элемент матрицы D[2][3] получает новое значение. Следующий шаг, когда условие также истинно привносит изменения в элемент, расположенный на пересечении второй строки и третьего столбца.
Список ребер
Список, в каждой строке которого записаны две смежные вершины и вес, соединяющего их ребра, называется списком ребер графа. Возьмем связный графG=(V, E), и множество ребер E разделим на два класса d и k, где d – подмножество, включающее только неориентированные ребра графа G, а k – ориентированные. Предположим, что некоторая величина p соответствует количеству всех ребер, входящих в подмножество d, а s – тоже относительно k. Тогда для графа G высота списка ребер будет равна s+p*2. Иными словами, количество строк в списке ребер всегда должно быть равно величине, получающейся в результате сложения ориентированных ребер с неориентированными, увеличенными вдвое. Это утверждение следует из сказанного ранее, а именно, что данный способ представления графа предусматривает хранение в каждой строке двух смежных вершин, а неориентированное ребро, соединяющее вершины v и u, идет как из v в u, так и изu в v.
Рассмотрим смешанный граф, в котором 5 вершин, 4 ребра и каждому ребру поставлено в соответствие некоторое целое значение (для наглядности оно составлено из номеров вершин):
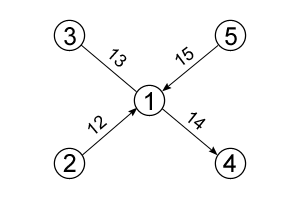
В нем 3 направленных ребра и 1 ненаправленное. Подставив значения в формулу, получим высоту списка ребер: 3+1*2=5.
Так выглядит список ребер для приведенного графа. Это таблица размером n×3, где n= s+p*2=3+1*2=5. Элементы первого столбца располагаются в порядке возрастания, в то время как порядок элементов второго столбца зависит от первого, а третьего от двух предыдущих.
Программная реализация списка ребер похожа на реализацию списка смежности. Так же как и в последней, в ней изначально необходимо организовать ввод данных, которые при помощи специальной функции будут распределяться по массивам. Второй шаг – вывести получившийся список смежности на экран.
В списке смежности хранились только смежные вершины, а здесь, помимо них, будут храниться веса инцидентных этим вершинам ребер, и для этой цели понадобиться дополнительный массив. К тому же, данный метод требует более строго порядка вывода вершин, т. к. если в списке смежности последовательность нарушалась лишь в строках, то использование аналогичного способа построения приведет к нарушению порядка в столбцах. Поэтому функцию добавления ребер следует организовать иначе.
Код программы на C++:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 | #include "stdafx.h"#include <iostream> using namespace std; const int Vmax=100, Emax=Vmax*(Vmax-1)/2; //в случае, если граф полный int terminal[Emax], weight[Emax], point[Emax]; int head[Vmax], last[Vmax]; int n, m, v, u, w, k=0, i; char r; void Add(int v, int u, int w) //добавление ребра { k=k+1; terminal[k]=u; weight[k]=w; //если вершина v новая, то//первая смежная ей вершина имеет номер k if (head[v]==0) head[v]=k; //если вершина v уже просматривалась, то//следующая смежная с ней вершина имеет номер k if (last[v]!=0) point[last[v]]=k; last[v]=k; } //главная функция void main() { setlocale(LC_ALL,"Rus"); cout<<"Кол. вершин >> "; cin>>n; cout<<"Кол. ребер >> "; cin>>m; cout<<"Вводите ребра и их вес (v, u, w):\n"; for (i=0; i<m; i++) { cin>>v>>u>>w; cout<<"Ребро ориент.? (y/n) >> "; cin>>r; if (r=='y') Add(v, u, w); else { Add(v, u, w); Add(u, v, w); } cout<<"..."<<endl; } m=m*2; //вывод списка ребер cout<<"Список ребер графа:\n"; for (i=0; i<m; i++) { k=head[i]; while (k>0) { cout<<"("<<i<<"->"<<terminal[k]<<")$="<<weight[k]<<endl; k=point[k]; } } system("pause>>void"); } |
Максимально возможное количество вершин в графе задано константой Vmax, а ребер – Emax. Последняя константа инициализируется формулой Vmax*(Vmax-1)/2, вычисляющей количество ребер в полном графе при известном числе вершин. Далее, в программах описываются 5 массивов:
· terminal – массив вершин, в которые входят ребра;
· weight – массив весов ребер;
· head[i]=k – хранит для i-ой вершины номер k-ого элемента массивов terminal и weight, где terminal[k] – первая вершина смежная с i-ой, а weight[k] – вес инцидентного ей ребра;
· last[i]=k – хранит для i-ой вершины номер k-ого элемента массивов terminal и weight, где terminal[k] – последняя вершина смежная с i-ой, а weight[k] – вес инцидентного ей ребра;
· point[i]=k – хранит для i-ой вершины номер k-ого элемента массивов terminal и weight, где terminal[k] – следующая вершина смежная с i-ой, а weight[k] – вес инцидентного ей ребра.
После ввода количества вершин (n) и ребер (m) графа, запускается цикл, на каждом шаге которого пользователь вводит с клавиатуры две смежные вершины и вес, лежащего между ними ребра. Если ребро является ориентированным, то функция добавления данных в список ребер (Add) вызывается один раз, если неориентированным – два раза. Общее число вызовов функции вычисляется все по той же формуле s+(p*2), где s – ориентированные ребра графа, p – неориентированные. Закончив формирование списка ребер, необходимо вдвое увеличить переменную m, т. к. в случае чисто неориентированного графа высота списка будет равна 0+(m*2).
Осталось вывести на экран получившуюся конструкцию. Вспомним, что на номер первой вершины смежной с i-ой вершиной указывает элемент head[i], следовательно, каждая новая итерация внешнего цикла должна начинаться с взятия этого номера (k=head[i]). Внутренний цикл перестанет выполняться тогда, когда не найдется ни одной смежной с i-ой вершины (k станет равной нулю), а внешний – по окончанию вывода списка ребер.
Рекомендуемые для просмотра задачи:
Задача 1
Пример. С помощью матрицы смежности найти компоненты сильной связности ориентированного графа D.
Выделим компоненты связности ориентированного графа, изображенного на рис. 1. В данной задаче количество вершин n=5.
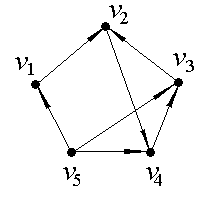
Рис. 1.
Значит, для данного ориентированного графа матрица смежности будет иметь размерность 5×5 и будет выглядеть следующим образом
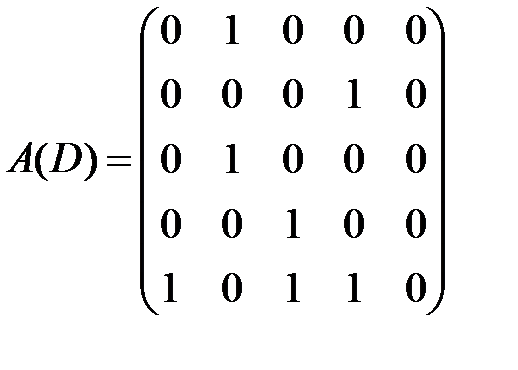 .
.
Найдем матрицу достижимости для данного ориентированного графа по формуле 1) из утверждения 3:
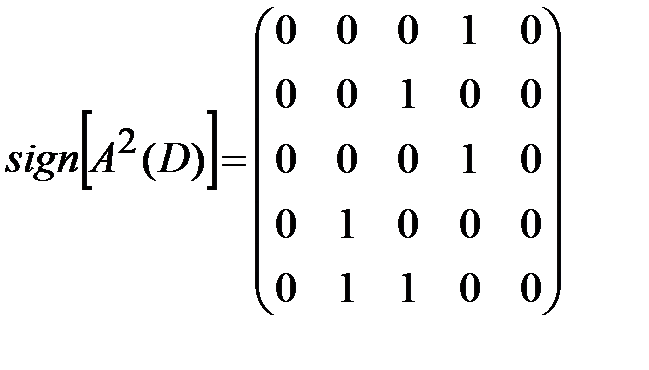 ,
, 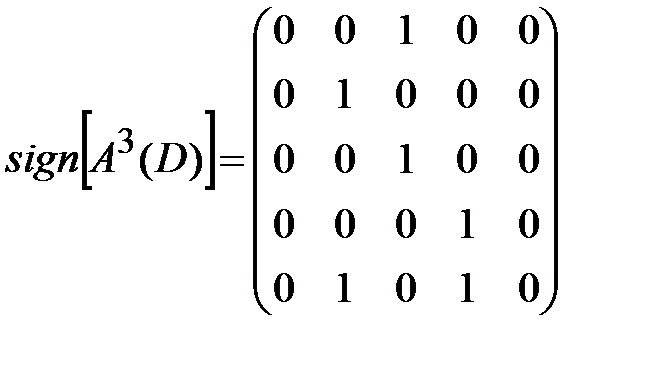 ,
,
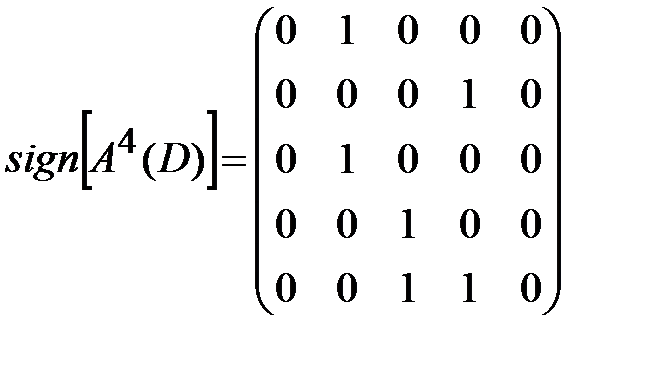 ,
,
Следовательно,
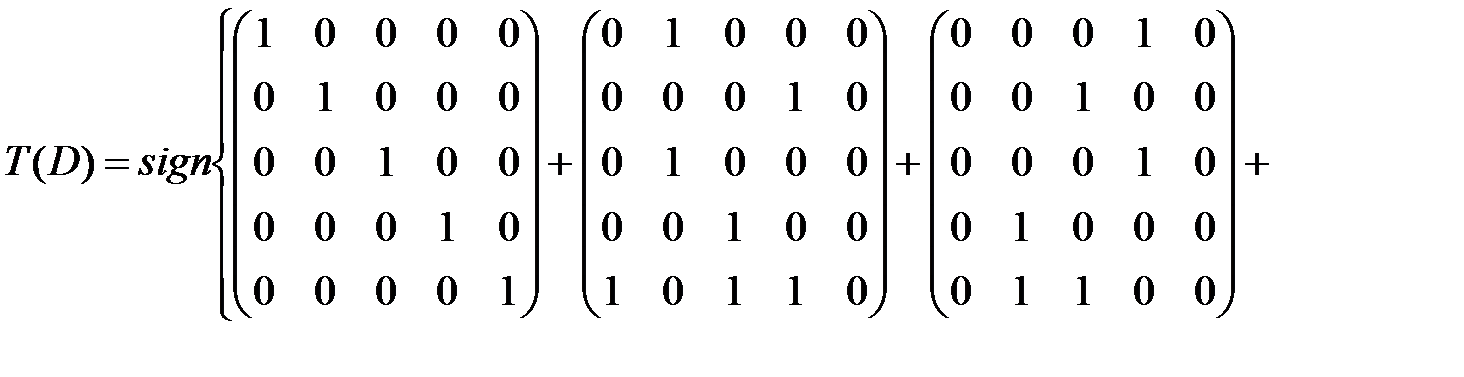
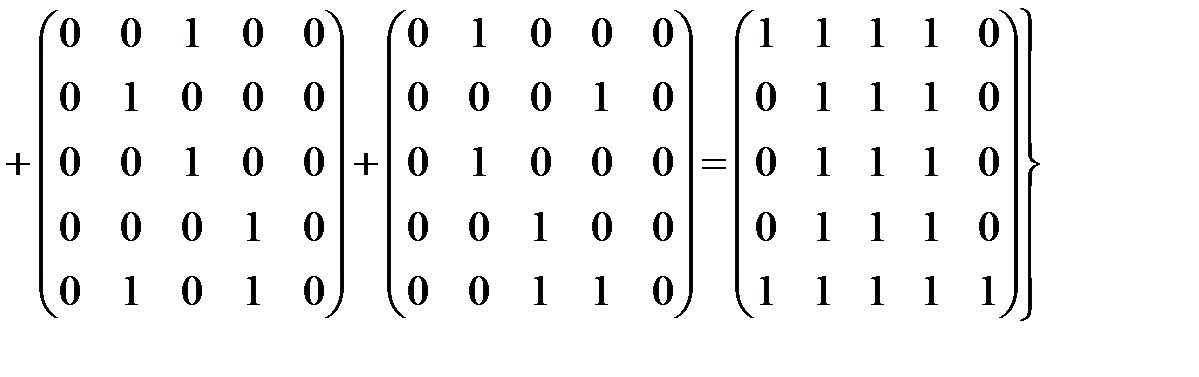 .
.
Таким образом, матрица сильной связности, полученная по формуле 2) утверждения 3, будет следующей:
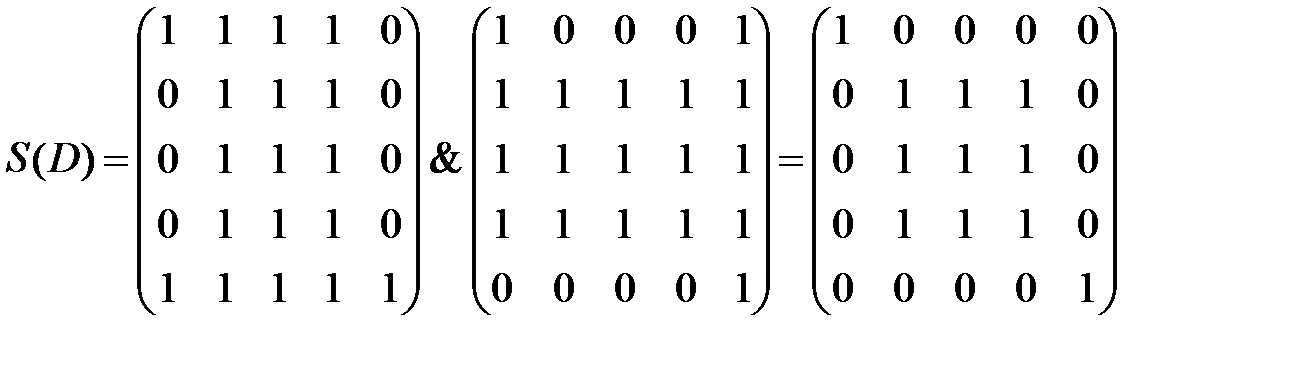 .
.
Присваиваем p=1 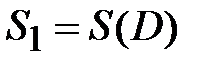 и составляем множество вершин первой компоненты сильной связности D1: это те вершины, которым соответствуют единицы в первой строке матрицы S(D). Таким образом, первая компонента сильной связности состоит из одной вершины
и составляем множество вершин первой компоненты сильной связности D1: это те вершины, которым соответствуют единицы в первой строке матрицы S(D). Таким образом, первая компонента сильной связности состоит из одной вершины 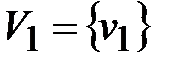 .
.
Вычеркиваем из матрицы S1(D) строку и столбец, соответствующие вершине v1, чтобы получить матрицу S2(D):
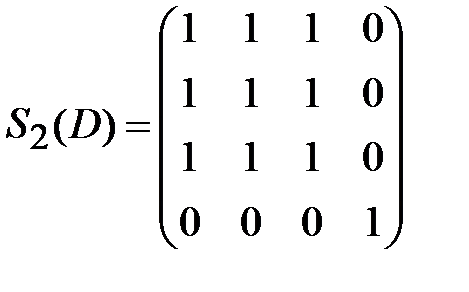 .
.
Присваиваем p=2. Множество вершин второй компоненты связности составят те вершины, которым соответствуют единицы в первой строке матрицы S2(D), то есть 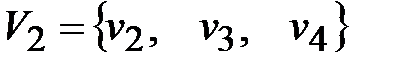 . Составляем матрицу смежности для компоненты сильной связности
. Составляем матрицу смежности для компоненты сильной связности 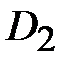 исходного графа D − в ее качестве возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V2:
исходного графа D − в ее качестве возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V2:
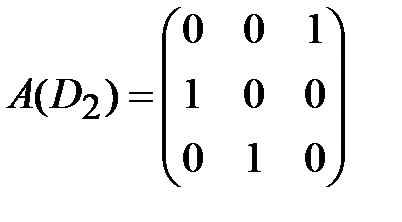 .
.
Вычеркиваем из матрицы S2(D) строки и столбцы, соответствующие вершинам из V2 ,чтобы получить матрицу S3(D), которая состоит из одного элемента:
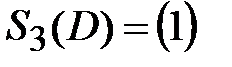
и присваиваем p=3. Таким образом, третья компонента сильной связности исходного графа, как и первая, состоит из одной вершины 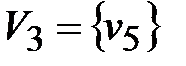 .
.
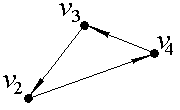
Таким образом, выделены 3 компоненты сильной связности ориентированного графа D:
D1:
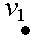
| D2:
| D3:
| |||
Задача 2
С помощью алгоритма фронта волны найти расстояния в ориентированном графе D: диаметр, радиус и центры, самый длинный путь
Пусть 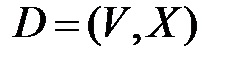 ориентированный граф с n³2 вершинами и v,w (v¹w) – заданные вершины из V.
ориентированный граф с n³2 вершинами и v,w (v¹w) – заданные вершины из V.
Алгоритм поиска минимального пути из 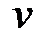 в
в 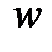 в ориентированном графе
в ориентированном графе
(алгоритм фронта волны).
1) Помечаем вершину 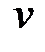 индексом 0, затем помечаем вершины Î образу вершины
индексом 0, затем помечаем вершины Î образу вершины 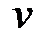 индексом 1. Обозначаем их FW1 (v). Полагаем k=1.
индексом 1. Обозначаем их FW1 (v). Полагаем k=1.
2) Если 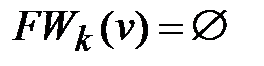 или k=n-1, и одновременно
или k=n-1, и одновременно 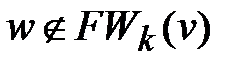 то вершина
то вершина 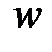 не достижима из
не достижима из 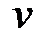 . Работа алгоритма заканчивается.
. Работа алгоритма заканчивается.
В противном случае продолжаем:
3) Если 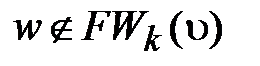 , то переходим к шагу 4.
, то переходим к шагу 4.
В противном случае мы нашли минимальный путь из 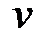 в
в 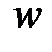 и его длина равна k. Последовательность вершин
и его длина равна k. Последовательность вершин
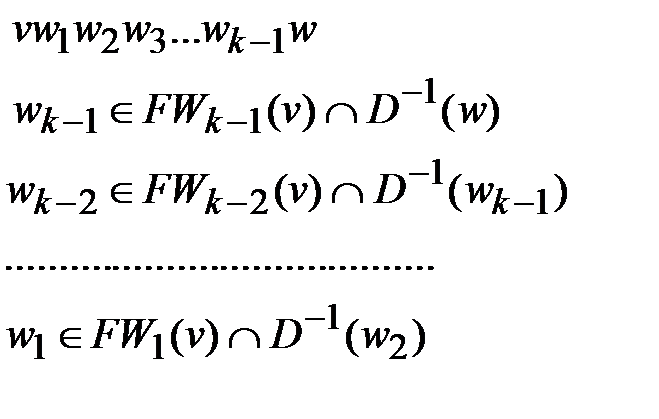
есть этот минимальный путь. Работа завершается.
4) Помечаем индексом k+1 все непомеченные вершины, которые принадлежат образу множества вершин c индексом k. Множество вершин с индексом k+1 обозначаем 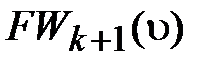 . Присваиваем k:=k+1 и переходим к 2).
. Присваиваем k:=k+1 и переходим к 2).
Замечания
· Множество 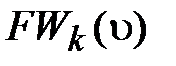 называется фронтом волны kго уровня.
называется фронтом волны kго уровня.
· Вершины 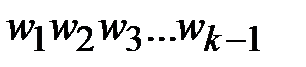 могут быть выделены неоднозначно, что соответствует случаю, если
могут быть выделены неоднозначно, что соответствует случаю, если 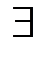 несколько минимальных путей из
несколько минимальных путей из 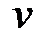 в
в 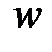 .
.
Чтобы найти расстояния в ориентированном графе, необходимо составить матрицу минимальных расстояний R(D)между его вершинами. Это квадратная матрица размерности 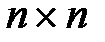 , элементы главной диагонали которой равны нулю (
, элементы главной диагонали которой равны нулю ( 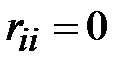 , i=1,..,n).
, i=1,..,n).
Сначала составляем матрицу смежности. Затем переносим единицы из матрицы смежности в матрицу минимальных расстояний ( 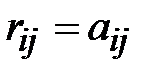 , если
, если 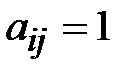 ). Далее построчно заполняем матрицу следующим образом.
). Далее построчно заполняем матрицу следующим образом.
Рассматриваем первую строку, в которой есть единицы. Пусть это строка − i-тая и на пересечении с j-тым столбцом стоит единица (то есть 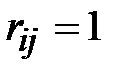 ). Это значит, что из вершины
). Это значит, что из вершины 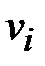 можно попасть в вершину
можно попасть в вершину 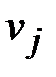 за один шаг. Рассматриваем j-тую сроку (строку стоит вводить в рассмотрение, если она содержит хотя бы одну единицу). Пусть элемент
за один шаг. Рассматриваем j-тую сроку (строку стоит вводить в рассмотрение, если она содержит хотя бы одну единицу). Пусть элемент 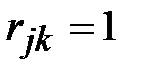 . Тогда из вершины
. Тогда из вершины 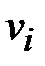 в вершину
в вершину 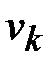 можно попасть за два шага. Таким образом, можно записать
можно попасть за два шага. Таким образом, можно записать 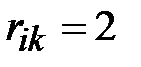 . Следует заметить, что если в рассматриваемых строках две или более единиц, то следует прорабатывать все возможные варианты попадания из одной вершины в другую, записывая в матрицу длину наикратчайшего из них.
. Следует заметить, что если в рассматриваемых строках две или более единиц, то следует прорабатывать все возможные варианты попадания из одной вершины в другую, записывая в матрицу длину наикратчайшего из них.
Примечание: В работе самый длинный путь найти при помощи алгоритма фронта волны.
Пример
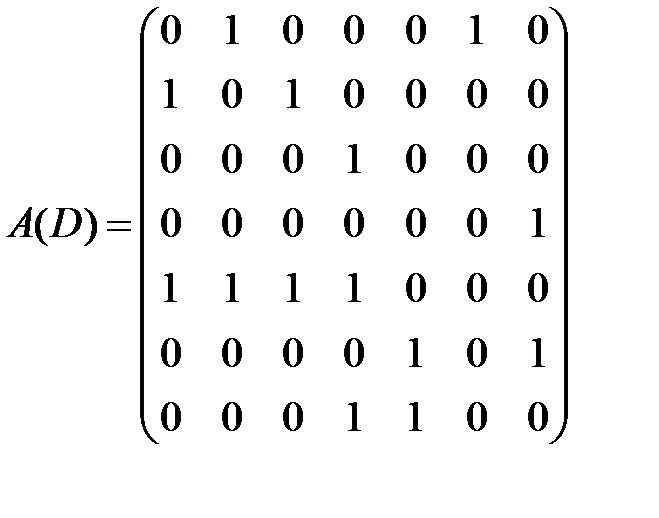
Найдем расстояния в ориентированном графе D, изображенном на рис. 1. В данной задаче количество вершин n=7, следовательно, матрицы смежности и минимальных расстояний между вершинами ориентированного графа D будут иметь размерность 7×7.
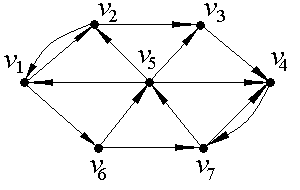
Рис.1.
Матрица смежности:
 .
.
Начинаем заполнять матрицу R(D) минимальных расстояний: сначала ставим нули по главной диагоналии rij=aij, если aij=1, (т.е. переносим единицы из матрицы смежности). Рассматриваем первую строку. Здесь есть две единицы, то есть из первой вершины за один шаг можно попасть во вторую и шестую. Из второй вершины можно попасть за один шаг в третью (путь в первую вершину нас не интересует), следовательно, можно записать 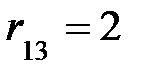 . Из шестой вершины можем добраться за один шаг в пятую и седьмую, а значит,
. Из шестой вершины можем добраться за один шаг в пятую и седьмую, а значит, 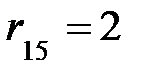 ,
, 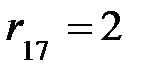 . Теперь ищем маршруты, исходящие из первой вершины, состоящие из 3 шагов: за 2 шага идем в третью вершину, оттуда за один шаг попадаем в четвертую, поэтому
. Теперь ищем маршруты, исходящие из первой вершины, состоящие из 3 шагов: за 2 шага идем в третью вершину, оттуда за один шаг попадаем в четвертую, поэтому 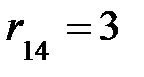 . В итоге получаем следующую матрицу:
. В итоге получаем следующую матрицу:

Таким образом, диаметром исследуемого ориентированного графа будет 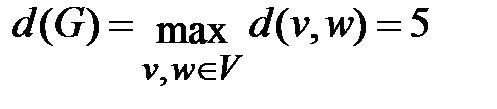 .
.
Для каждой вершины заданного ориентированного графа найдем максимальное удаление (эксцентриситет) в графе G от вершины нее по формуле, которая была приведена выше 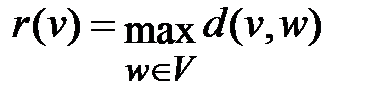 : r(vi) − максимальное из расстояний, стоящих в i-той строке. Таким образом,
: r(vi) − максимальное из расстояний, стоящих в i-той строке. Таким образом,
r(v1)=3, r(v2)=3, r(v3)=5, r(v4)=4, r(v5)=2, r(v6)=2, r(v7)=3.
Значит, радиусомграфа G будет 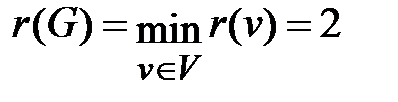
Соответственно, центрами графа G будут вершины v5 и v6 , так как величины их эксцентриситетов совпадают с величиной радиуса 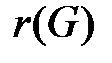 .
.
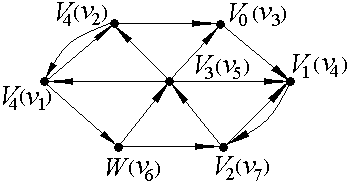
Опишем теперь нахождение минимального пути из вершины v3 в вершину v6 по алгоритму фронта волны. Обозначим вершину v3 как V0, а вершину v6 - как W (см. рис.1.2). Множество вершин, принадлежащих образу V0, состоит из одного элемента - это вершина v4, которую, согласно алгоритму, обозначаем как V1: FW1(v3)={v4}. Поскольку искомая вершина не принадлежит фронту волны первого уровня 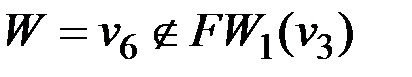 , продолжаем работу алгоритма. Строим фронт волны второго уровня - это множество вершин, принадлежащих образу вершины V1: FW2(v3)={v7}, обозначаем v7≡V2. В образ вершины V2 входят две вершины - v5 и v4, но, так как v4 уже была помечена как V0, то фронт волны третьего уровня состоит из одного элемента: FW3(v3)={v5}, v5≡V3. Из непомеченных вершин в образ вершины V3 входят v1 и v2, соответственно, FW4(v3)={v1, v2}, v1≡V4, v2≡V4. Теперь помечены все вершины, кроме v6, которая входит в образ вершины
, продолжаем работу алгоритма. Строим фронт волны второго уровня - это множество вершин, принадлежащих образу вершины V1: FW2(v3)={v7}, обозначаем v7≡V2. В образ вершины V2 входят две вершины - v5 и v4, но, так как v4 уже была помечена как V0, то фронт волны третьего уровня состоит из одного элемента: FW3(v3)={v5}, v5≡V3. Из непомеченных вершин в образ вершины V3 входят v1 и v2, соответственно, FW4(v3)={v1, v2}, v1≡V4, v2≡V4. Теперь помечены все вершины, кроме v6, которая входит в образ вершины 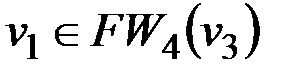 , то есть FW5(v3)={v6≡W}, работа алгоритма закончена. Минимальный путь (5 шагов) из вершины v3 в вершину v6 выглядит так: v3 v4 v7 v5 v1 v6.
, то есть FW5(v3)={v6≡W}, работа алгоритма закончена. Минимальный путь (5 шагов) из вершины v3 в вершину v6 выглядит так: v3 v4 v7 v5 v1 v6.
Задача3 Найти Эйлерову цепь в неориентированном графе.
Исходя из утверждений 1 и 2, чтобы найти Эйлерову цепь, нужно соединить две вершины с нечетными степенями фиктивным ребром. Тогда задача сводится к нахождению Эйлерова цикла по приведенному ниже алгоритму. Из найденного цикла удаляется фиктивное ребро, тем самым находится искомая Эйлерова цепь.
Дата добавления: 2017-05-02; просмотров: 8455;











