Кинематическая схема балансирного станка-качалки

Кинематическая схема балансирного станка-качалки представляет собой четырёхзвенник ОВСD.

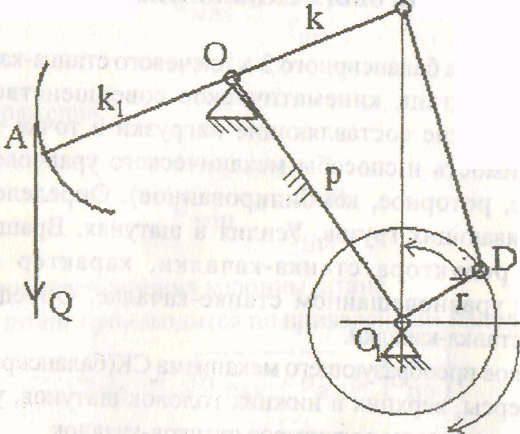Неподвижное звено – ОD, подвижные звенья – кривошип (r), шатун (l) и заднее плечо балансира (b). При вращении кривошипа точка С описывает окружность радиуса r, а точка В движется по дуге радиуса b.

Определим закон движения точки В, но для упрощения сделаем некоторые допущения, а именно:

- точка В движется не по дуге, а по прямой;

- радиус кривошипа намного меньше длины балансира;

- угол β, образованный шатуном и линией, соединяющей центр кривошипа с точкой В, принимается равным нулю;

тогда, закон движения т. В соответствует закону движения поршня насоса с кривошипно-шатунным механизмом или S_В = r (l – cos α).

Скорость движения точки В будет равна:

v_B = ω r sin α,

а ускорение:

w_B = ω² r cos α.

Тогда путь, скорость и ускорение т. А определяются соотношением плеч балансира а и b :

S_A = 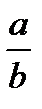r( l- cos α)

v_A = 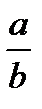ω r sin α

w_A = 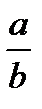ω² r cos α,

где ω – угловая скорость вращения кривошипа.

Графики изменения скорости и ускорения точки подвеса колонны штанг – это синусоида и косинусоида соответственно.

Более точно закономерность изменения перемещения, скорости и ускорения точки подвеса штанг может быть определена с помощью приближенного расчета.

Кинематическое совершенство станка-качалки характеризуется коэффициентом m, который определяется по формуле:

m = ,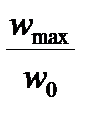

где w_max – максимальное ускорение точки подвеса штанг станка-качалки; w₀ – ускорение при гармоничном движении.

Для определения показателя m удобно пользоваться следующей формулой:

m =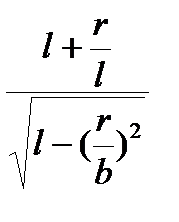

В зависимости от глубины подвески насоса допустимый коэффициент кинематического совершенства изменяется и для глубоких скважин должен быть не более 1,3.

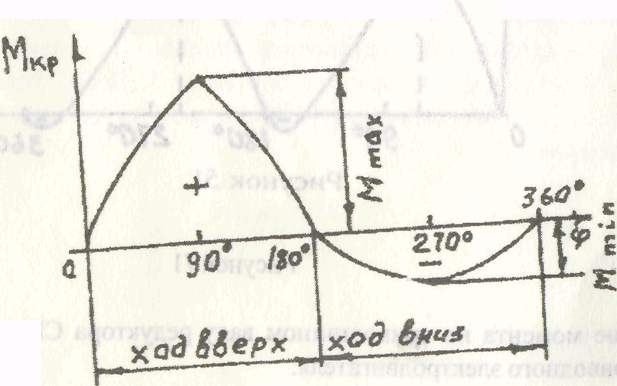
Нагрузки на головку балансира СК складываются из статических (вес столба жидкости и колонны штанг) и динамических (от движущихся масс столба жидкости и колонны штанг). Максимальные нагрузки возникают при ходе вверх и определяются:

P_max = P_ж + Р_шт + Р_жi + P_штi + R