Второе начало термодинамики
ЭнтропияS как функция равновесного состояния термодинамической системы вводится на основе равенства Клаузиуса
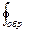
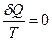
для обратимых круговых процессов. Здесь 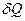 - количество теплоты, которое получает
- количество теплоты, которое получает 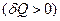 или отдает
или отдает 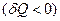 система на бесконечно малом участке кругового процесса при температуре T.
система на бесконечно малом участке кругового процесса при температуре T.
Согласно определению разность энтропии 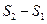 в равновесных состояниях 1 и 2 описываются выражением
в равновесных состояниях 1 и 2 описываются выражением
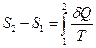 .
.
Интеграл в правой части вычисляется для любого обратимого процесса, переводящего систему из равновесного состояния 1 в равновесное состояние 2. С помощью первого начала термодинамики интеграл в правой части можно переписать следующим образом
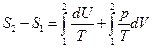 ,
,
где U - внутренняя энергия системы, p - давление и V - объём.
В классической термодинамике определяется только разность энтропии в двух произвольных равновесных состояний, поэтому энтропия равновесного состояния задана с точностью до постоянной. Размерность энтропии в СИ Дж/К.
Задача №12
Определить изменение 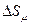 энтропии 1 моля идеального газа при 1)изохорном, 2) изобарном, 3) изотермическом и 4) адиабатном процессах.
энтропии 1 моля идеального газа при 1)изохорном, 2) изобарном, 3) изотермическом и 4) адиабатном процессах.
Решение
Задача решается на основе определения энтропии
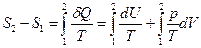 , (5.12.1)
, (5.12.1)
уравнение Клапейрона - Менделеева для 1 моля идеального газа
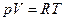 (5.12.2)
(5.12.2)
и формулы, описывающей внутреннюю энергию 1 моля одноатомного идеального газа,
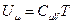 , (5.12.3)
, (5.12.3)
где 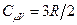 – молярная теплоёмкость идеального одноатомного газа при постоянном объёме.
– молярная теплоёмкость идеального одноатомного газа при постоянном объёме.
1) Изохорный процесс 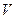 =const. Из (4.1) и (4.3) следует, что
=const. Из (4.1) и (4.3) следует, что
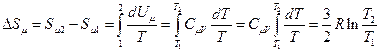 , (5.12.4)
, (5.12.4)
где 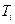 – температура газа в i-ом состоянии, i=1,2.
– температура газа в i-ом состоянии, i=1,2.
2) Изобарный процесс 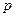 =const. Согласно (4.1) - (4.3)
=const. Согласно (4.1) - (4.3)
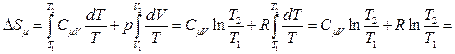
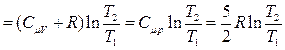 . (5.12.5)
. (5.12.5)
Здесь 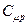 – молярная теплоёмкость идеального одноатомного газа при постоянном давлении. В преобразованиях (4.5) использовано соотношение
– молярная теплоёмкость идеального одноатомного газа при постоянном давлении. В преобразованиях (4.5) использовано соотношение
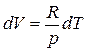 ,
,
которое получается для изобарного процесса из уравнения Клапейрона – Менделеева (5.12.2).
3) Изотермический процесс 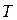 =const. Используя (5.12.1) и (5.12.2), находим
=const. Используя (5.12.1) и (5.12.2), находим
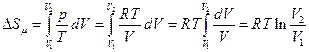 , (5.12.6)
, (5.12.6)
где Т - температура изотермического процесса и 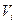 – объем газа в i-ом состоянии , i=1,2 .
– объем газа в i-ом состоянии , i=1,2 .
4) Адиабатный процесс 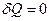 . По определению энтропии и адиабатного процесса
. По определению энтропии и адиабатного процесса
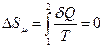 .
.
Ответ: 1) 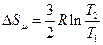 , 2)
, 2) 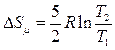 , 3)
, 3) 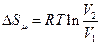 , 4)
, 4) 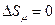 .
.
Задача №13
Определить изменение 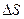 энтропии 1 моля вещества при 1) плавлении, если удельная теплота плавления
энтропии 1 моля вещества при 1) плавлении, если удельная теплота плавления 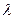 , температура плавления
, температура плавления 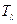 и 2) испарении, если удельная теплота испарения (парообразования)
и 2) испарении, если удельная теплота испарения (парообразования) 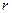 , температура кипения
, температура кипения 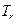 . Молярная масса вещества
. Молярная масса вещества 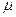 .
.
Решение
Задача решается на основе формул для приращения энтропии
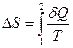 , (5.13.1)
, (5.13.1)
молярной теплоты плавления
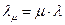 (5.13.2)
(5.13.2)
и молярной теплоты испарения (парообразования)
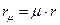 . (5.13.3)
. (5.13.3)
1) Плавление происходит при постоянной температуре 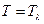 , поэтому из (5.13.1) и (5.13.2) следует, что
, поэтому из (5.13.1) и (5.13.2) следует, что
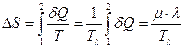 . (5.13.4)
. (5.13.4)
2) Кипение происходит при постоянной температуре 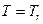 , поэтому из (5.13.1) и (5.13.2) получаем, что
, поэтому из (5.13.1) и (5.13.2) получаем, что
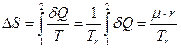 . (5.13.5)
. (5.13.5)
Оба процесса протекают при получении веществом теплоты извне, поэтому энтропия увеличивается.
Ответ: 1) 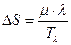 , 2)
, 2) 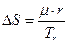 .
.
Задача №14
Два тела, имеющие массы m1 и m2, температуры 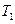 и
и 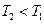 и одинаковую удельную теплоёмкость c, помещены в теплоизолирующую оболочку. Определить равновесную температуру
и одинаковую удельную теплоёмкость c, помещены в теплоизолирующую оболочку. Определить равновесную температуру 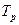 тел и изменение
тел и изменение 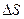 суммарной энергии системы при установлении равновесия.
суммарной энергии системы при установлении равновесия.
Решение
Начальное состояние тел не является равновесным, поскольку 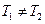 . За счет теплопроводности при непосредственном контакте тел или лучистого теплообмена тела переходят в равновесное состояние, где они имеют одинаковую температуру Тр.
. За счет теплопроводности при непосредственном контакте тел или лучистого теплообмена тела переходят в равновесное состояние, где они имеют одинаковую температуру Тр.
Расчеты выполняются на основе закона сохранения энергии и определения энтропии.
Если температура тела 1 уменьшилась от 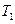 до
до 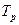 , то тело 1 передало телу 2 количество теплоты
, то тело 1 передало телу 2 количество теплоты
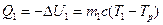 , (5.14.1)
, (5.14.1)
которое пошло на увеличение, 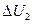 внутренней энергии этого тела
внутренней энергии этого тела
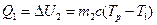 . (5.14.2)
. (5.14.2)
Из (5.14.1)и (5.14.2) следует, что равновесная температура двух тел
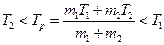 . (5.14.3)
. (5.14.3)
Изменение энтропия тела 1 в случае обратимого охлаждения от 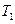 до
до 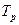 описывается выражением
описывается выражением
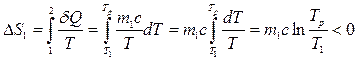 . (5.14.4)
. (5.14.4)
Изменение энтропия тела 2 в случае обратимого нагревания от 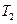 до
до 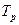 определяется формулой
определяется формулой
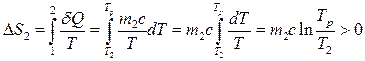 . (5.14.5)
. (5.14.5)
Полное изменение энтропии двух тел
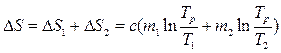 . (5.14.6)
. (5.14.6)
Поскольку в случае 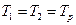
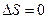 и
и 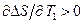 при
при 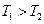 , то
, то 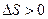 в полном соответствии со вторым началом термодинамики.
в полном соответствии со вторым началом термодинамики.
Ответ: 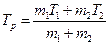 ,
, 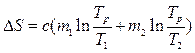 .
.
Процессы переноса
В отсутствии внешнего силового поля равновесное состояние системы характеризуется постоянными по всему объему системы средними значениями концентрации частиц n и температуры Т. Если отклонения от равновесия невелики, можно ввести представление о локальном равновесии в малых макроскопических областях системы. Каждая такая область характеризуется своими величинами концентрации и температуры. Благодаря хаотическому тепловому движению частиц в неравновесной системе самопроизвольно (спонтанно) формируются процессы переноса вещества (диффузия) и внутренней энергии, зависящей от температуры (теплопроводность). Эти процессы переноса стремятся выравнить значения n и Т по всему объему системы и перевести систему в равновесное состояние.
В задачах рассматриваются стационарные (не зависящие от времени) процессы диффузии и теплопроводности в идеальном газе. Допустим, что процессы переноса происходят только вдоль оси х. Диффузия описывается законом Фика
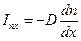 ,
,
где 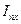 – плотность потока частиц вдоль оси x (число частиц, проходящих за единицу времени через единичное поперечное сечение, перпендикулярное оси x), D – коэффициент диффузии, n – концентрация частиц. Теплопроводность определяется законом Фурье
– плотность потока частиц вдоль оси x (число частиц, проходящих за единицу времени через единичное поперечное сечение, перпендикулярное оси x), D – коэффициент диффузии, n – концентрация частиц. Теплопроводность определяется законом Фурье
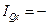 ǽ
ǽ 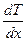 ,
,
где 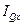 – плотность потока теплоты вдоль оси x (количество теплоты, переносимой за единицу времени через единичное поперечное сечение, перпендикулярное оси x), ǽ – коэффициент теплопроводности, Т – температура.
– плотность потока теплоты вдоль оси x (количество теплоты, переносимой за единицу времени через единичное поперечное сечение, перпендикулярное оси x), ǽ – коэффициент теплопроводности, Т – температура.
В равновесном состоянии 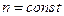 ,
, 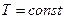 , поэтому
, поэтому 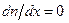 и
и 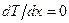 , а потоки частиц и теплоты обращаются в нуль.
, а потоки частиц и теплоты обращаются в нуль.
Задача №15
Для случая идеального газа получить формулы для коэффициентов диффузии D и теплопроводности ǽ.
Решение
Задача нахождения величины D решается с помощью закона Фика
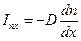 . (6.15.1)
. (6.15.1)
Пусть распределение частиц по скоростям теплового движения является изотропным, т.е. все направления движения произвольной частицы равновероятны. В этом случае плотность потока частиц в направлении оси x описывается формулой
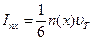 , (6.15.2)
, (6.15.2)
где 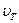 – средняя скорость теплового движения,
– средняя скорость теплового движения, 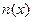 – концентрация частиц в точке
– концентрация частиц в точке 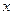 . Температура газа Т и, следовательно, скорость
. Температура газа Т и, следовательно, скорость 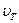 одинаковые для всех элементов газа. Распределение Максвелла по скоростям является изотропным.
одинаковые для всех элементов газа. Распределение Максвелла по скоростям является изотропным.
Если концентрация 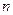 зависит от координаты
зависит от координаты 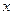 (см. рисунок),
(см. рисунок),
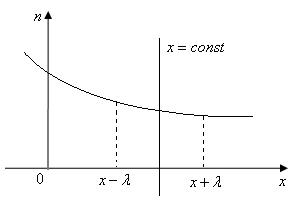
суммарная плотность потока частиц в направлении оси x имеет вид
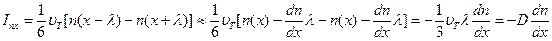 . (6.15.3)
. (6.15.3)
Отсюда находим, что
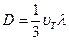 . (6.15.4)
. (6.15.4)
Здесь 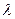 – средняя длина свободного (без столкновений) пробега частиц.
– средняя длина свободного (без столкновений) пробега частиц.
Дата добавления: 2021-07-22; просмотров: 545;











