Наклонно-направленных скважин по методу Борисова

Одиночная горизонтальная скважина[28, 2].Рассмотрим горизонтальную скважину длиной 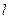радиуса 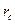, расположенную в центре однородного изотропного пласта с круговым контуром питания 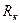, на котором задано давление 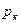. Давление на забое скважины 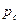. Пласт и содержащуюся в нем жидкость предполагаем несжимаемыми.

Полное фильтрационное сопротивление можно представить суммой двух сопротивлений: внешнего – от контура питания до прямолинейной вертикальной галереи, совпадающей с проекциями горизонтальной скважины на кровлю (или подошву) пласта, и внутреннего, обусловленного тем, что мы имеем в действительности не галерею, а скважину.

Внешнее сопротивление определяем по формуле:

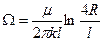. (2.31)

Внутренне сопротивление определяем так же, как и для одной вертикальной скважины в батарее, приняв, что мощность рассматриваемого пласта соответствует расстоянию между скважинами, а длина ствола горизонтальной скважины равна мощности в случае вертикальной скважины. Тогда

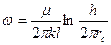. (2.32)

Эту же формулу можно получить, разрезав горизонтальную скважину на отрезки длиной, равной мощности пласта 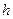, и повернув каждый из них до вертикального положения. При этом будем иметь батарею вертикальных скважин, расстояние между которыми равно 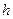, а их число .

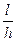Сумма указанных сопротивлений даст нам отношение перепада давления к дебиту горизонтальной скважины

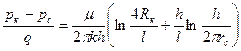. (2.33)

Одиночная наклонная скважина или один куст наклонных скважин.При рассмотрении наклонной скважины галерея будет проходить через ось скважины и будет равна величине 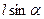( 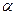- угол отклонения скважины от вертикали). При определении внутреннего сопротивления можно также «разрезать» наклонную скважину на отрезки длиной 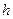и ставить их вертикально, то есть используется принятая ранее схематизация течения жидкости к такой скважине. При этом расстояние между скважинами будет 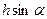. Тогда расчетная формула для куста с наклонными скважинами примет вид

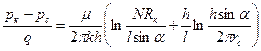. (2.34)

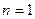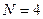Частный случай единичной наклонной скважины можно получить из (2.34), положив и . Кроме того, приняв 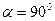, получим формулу для горизонтальных скважин (2.33).

Таким образом, формулу (2.34) можно считать общей для одиночных кустов или одиночных горизонтальных и наклонных скважин.