Краткий анализ эффективности работы наклонных и горизонтальных скважин

Вопросам притока к пологим и горизонтальным нефтяным и газовым скважинам посвящены работы З.С. Алиева, E.G. Anklam, К.С. Басниева, D.K. Babu, Ю.Е. Батурина, Ю.П. Борисова, Г.Г. Вахитова, F.M. Giger, P.A. Goode, M.J. Economaides, S.D. Joshi, F.J. Kuckuk, В.Д. Лысенко, Р.И. Медведского, В.П. Меркулова, A.S. Odeh, В.П. Пилатовского, А.М. Пирвердяна, П.Я. Полубариновой-Кочиной, D.W. Peaceman, Е.Ю. Проселкова, А.Д. Седых, Ю.И. Стклянина, А.П. Телкова, В.П. Табакова, К.М. Тагирова, К.М. Федорова, В.В. Шеремета, В.Н. Щелкачева, И.А. Чарного, В.А. Черных, H. Yuan и других исследователей [1,2,68,35,36,5,6,7,9,11,12,13,44,75,102,20].

Для дебита нефтяной пологой и горизонтальной скважин получены решения в различных постановках. Однако, с учетом всех видов гидравлических сопротивлений ствола, решений нет. Это же относится и к пологим, и к горизонтальным газовым скважинам.

На основе имеющихся теоретических исследований и накопленного практического опыта выделяют следующие основные объекты и направления применения горизонтальных скважин:

-маломощные пласты (5-10 м) с низкой и неравномерной проницаемостью;

-объекты с подошвенной водой и верхним газом с целью ограничения конусообразования;

-коллекторы с вертикальной трещиноватостью;

-разработка месторождений высоковязких нефтей и битумов, шельфовых и труднодоступных продуктивных зон.

На практике применяются следующие определения скважин, различающихся по способу проводки и конструкции:

· вертикальными скважинами называются скважины, в которых проектом бурения не предусматривается целенаправленной отклонение ствола от вертикали. В процессе проводки могут иметь место случайные отклонения от вертикали за счет естественного искривления;

· наклонно-направленными называются скважины, в которых проектом бурения предусматривается отклонение ствола от вертикали по заданной кривой в соответствующем азимуте;

· горизонтальными называются скважины, в которых интервал вскрытия продуктивного пласта стволом скважины более чем в два раза превышает толщину пласта;

· разветвлено-горизонтальными скважинами называются такие скважины, в вертикальной части которых в точках, расположенных выше продуктивного пласта, забуривается несколько наклонных стволов, каждый из которых имеет интервал продуктивного пласта не менее чем в два раза превышающего его толщину. Каждая разветвлено-горизонтальная скважина должна иметь возможность установления независимого, контролируемого и управляемого режима эксплуатации с помощью технических средств, называемых узлами разветвления.

Если протяженность горизонтального участка не превышает более чем в два раза толщину пласта, такие скважины называются разветвленными наклонно-горизонтальными.

Многозабойными называются скважины, когда забуривание дополнительных стволов проводится в точках, находящихся в пределах продуктивного пласта. Если протяженность дополнительных стволов превышает более чем в два раза толщину пласта, скважины называют многозабойными горизонтальными.

Как видно, данные определения не охватывают весь диапазон возможных траекторий стволов скважин по пласту. В последнее время в научной литературе появились такие термины как «пологая» и «субгоризонтальная» скважины. Существуют следующие определения скважин по траекториям: «наклонно направленная» - с зенитным углом 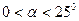; «пологая» - скважина с зенитным углом 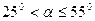; «горизонтальная» - скважина с зенитным углом 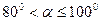. Между тем термин «наклонно направленная» скважина применяется так же для скважин при кустовом способе бурения, в случае, если они отходят от вертикали в верхней части своей траектории вне пласта.

Вопросам притока к горизонтальным скважинам посвящено большое количество научных работ [28]. При этом весьма ограниченное число работ посвящено горизонтальным газовым и газоконденсатным скважинам и практически не исследованы вопросы притока к пологим нефтяным и газовым скважинам. Одни из первых работ по гидродинамике притока жидкости к горизонтальным скважинам были опубликованы в нашей стране.

И.А. Чарный исследовал установившийся приток к горизонтальной скважине в изотропном пласте в случаях симметричного и несимметричного расположения скважины по толщине пласта и получил следующие зависимости [18; 19]:

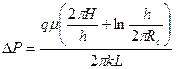; (1.1)

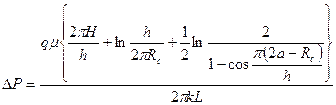. (1.2)

Он исследовал приток к горизонтальной скважине при следующих предположениях, что пласт считался однородным, полубесконечным, контур питания прямолинейным. Формулы притока (1.1) и (1.2) позволяют вычислить удельный дебит горизонтальной скважины по жидкости при различных расположениях скважин в изотропном по проницаемости пласте. Ось скважины находится на расстоянии a от кровли пласта.

Позднее А.М. Пирвердян продолжил исследования И.А. Чарного по притоку жидкости к горизонтальной скважине, но рассматривал анизотропный пласт и нашел следующее решение поставленной задачи методом зеркального отражения источников-стоков [12, 13]:

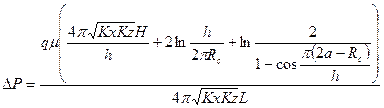. (1.3)

Выражение (1.3) получено в предположении, что горизонтальная скважина имеет большую протяженность, при котором можно пренебречь искривлением линии тока, вследствие конечности длины горизонтального участка скважины. Как правило, данное допущение является корректным и позволяет использовать (1.3) в качестве основной методики при интерпретации результатов исследования горизонтальной скважины в установившихся режимах фильтрации.

Однако следует учитывать, что работы И.А. Чарного и А.М. Пирвердяна посвящены вопросам притока жидкости к горизонтальным скважинам бесконечной длины в пластах конечной толщины. Кроме того, полученные зависимости пригодны только для полосовой залежи.

Результатами теоретических исследований, проведенных позднее П.Я. Полубариновой-Кочиной [15, 16], можно пользоваться лишь при условии, что толщина пласта во много раз превосходит длину ствола скважины. Если же толщина пласта соизмерима с длиной наклонной скважины, то формулами пользоваться нельзя. В этих же работах исследуется процесс трехмерной фильтрации в пластах, толщины которых во много раз превосходят длину наклонной скважины. Задача об установившемся притоке жидкости к горизонтальным и наклонным скважинам решилась Полубариновой-Кочиной также и экспериментально.

В.И. Щypов проводил исследование дебита наклонных и горизонтальных скважин на основе электролитической модели, что представляет особый интерес [22]. Новизна обработки результатов экспериментов заключается в том, что в знаменатель формулы Дюпюи вводится слагаемое С, характеризующее гидродинамическое совершенство скважины. Его значение определяется путем сравнения дебитов горизонтальных и наклонных скважин с дебитом вертикальных скважин при различных значениях длинах стволов, мощностей пласта, углов наклона стволов и т.д. Если величина параметра С отрицательна, то это означает, что дебит наклонных и горизонтальных скважин при прочих равных условиях выше дебита вертикальных скважин.

В дальнейшем В.П. Меркулов получил полуэмпирические формулы для расчета дебитов, которые не требуют использования каких-либо дополнительных графиков или таблиц [6]. Но следует учитывать, что они имеют определенные пределы применимости, полученные на основе экспериментальных данных, а потому судить о погрешностях расчетов, проводимых по предложенным автором формулам вне этих пределов, затруднительно.

В работе В.П. Меркулова, М.Л. Сургучева [7] получены формулы для определения производительности наклонных скважин в слоистом пласте. Полученные ими формулы дают хорошее совпадение с данными экспериментов, полученных электролитической модели. При выводе формул были приняты следующие допущения: 1) послойное допущение; 2) положение о равенстве отношения дебитов вертикальных скважин к дебиту вертикальной галереи и отношения дебитов наклонных скважин к дебиту наклонной галереи. Эти допущения, как правило, приводят к занижению до 8-10% экспериментальных результатов, что для практических целей вполне допустимо.

Значительное число работ по созданию теоретических основ разработки нефтяных месторождений с помощью наклонных, горизонтальных и многозабойных скважин выполнено Ю.П. Борисовым, В.П. Пилатовским, В.П. Табаковым [2, 9, 11, 17]. Наибольший практический интерес представляет методика определения производительности горизонтальной скважины, вскрывшей полосообразный нефтегазовый пласт с подошвенной водой, при стационарном режиме фильтрации.

В.П. Табаков рассмотрел установившийся приток жидкости к одиночным наклонным, многозабойным скважинам и скважинам сложного профиля в слоистом горизонтальном пласте, оценил эффективность этих скважин, а также решил задачи о притоке жидкости к батарее наклонных и двухзабойных скважин [17].

В.П. Пилатовский [9] предложил общую гидродинамическую теорию притока однородной жидкости к горизонтальным скважинам ограниченной протяженности, пробуренным в горизонтальном пласте постоянной толщины. В этой работе проведено дальнейшее развитие предложенной теории и приводится ряд новых результатов.

В работах [11] изложены способы учета интерференции многозабойных скважин с горизонтальными и пологонаклонными стволами.

Ю.П. Борисов и В.П. Табаков предложили простой способ расчета взаимодействия многозабойных скважин. При этом за радиус скважин следует принимать некоторый эквивалентный радиус, величина которого определена [27].

Обобщая ранний этап исследований горизонтальных скважин, объективно следует заметить, что во всех перечисленных выше зависимостях исследовано плоское течение, хотя приток к наклонным и горизонтальным скважинам в большинстве случаев происходит с участием вертикальной составляющей потока. Однако получение простых расчетных формул при учете вертикальной составляющей потока сопряжено с определенными математическими трудностями.

В дальнейшем интерес к исследованию притока к горизонтальным скважинам в нашей стране заметно уменьшился, и впоследствии был возобновлен многими зарубежными учеными. Следует отметить, что уже к началу 80-х за рубежом появились сообщения о крупных достижениях по увеличению производительности скважин благодаря горизонтальному бурению. Был опубликован целый ряд работ, посвященных поведению коллектора, вскрытого вертикальными и горизонтальными скважинами и сопоставлению показателей работы этих скважин.

Аналитическая модель двухфазного течения рассмотрена в работе B. Karcher, F. Giger, J. Combe, которую можно отнести к числу исследований стационарного притока к горизонтальной скважине. Полосообразный нефтяной пласт с подошвенной водой вскрыт горизонтальной скважиной непосредственно у кровли. В этой работе рассматривается двухмерное движение несжимаемых жидкостей в плоскости, перпендикулярной оси скважины, в условиях поршневого вытеснения. В качестве решения был применен метод годографа, предложенный M. Muskat и R. Kidder. В последствии данный метод использовался при решении аналогичных задач Д.А. Эфросом.

Работа авторов F. Kuchuk, P. Good, B. Brice [102] отличается от всех публикаций описанных выше, нестационарностью процесса фильтрации, а поэтому представляет особый интерес. В ней приводится решение дифференциального уравнения в частных производных, описывающего трехмерную нестационарную фильтрацию упругой жидкости, которое имеет вид:

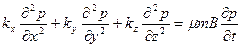. (1.4)

Уравнение (1.4) полностью идентично уравнению, описывающему аналогичный процесс к вертикальной скважине. Областью интегрирования уравнения (1.4) является полосообразный пласт.

Решение уравнения (1.4) отыскивается с помощью метода разделения переменных, для чего вводится ряд допущений. Далее нестационарная фильтрация замещается квазистационарной и дебит горизонтальной скважины определяется по формуле:

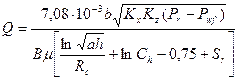, (1.5)

где

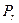- среднее пластовое давление в объеме дренирования;

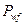- среднее давление по длине горизонтального ствола;

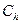- геометрический фактор;

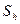- скин-эффект.

Геометрический фактор 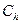рассчитывается в работе D. Peaceman по следующей зависимости:

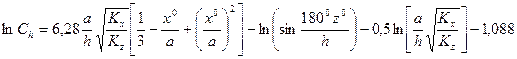. (1.6)

В большинстве случаев, встречающихся в инженерной практике, длина горизонтальной скважины 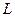составляет более 50% размера полосообразного пласта, при этом погрешность в расчетах дебитов по формуле (1.5) не превышает 3%. При снижении величины вскрытия полосообразного пласта погрешность в определении дебитов может доходить до 10%.

Что касается режима неустановившейся фильтрации, то в последнее время эта проблема привлекает значительное внимание, в связи с необходимостью получения простых и точных зависимостей, позволяющих на практике осуществлять гидродинамические исследования скважин.

В численном моделировании путем применения конечных разностей, модели скважины используются для определения соотношения между давлением на забое скважины, и давлением, вычисленным для блока, содержащего скважину.

При однофазном потоке модель вертикальной скважины предложена D. Peaceman:

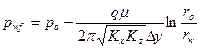, (1.7)

где 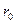- эквивалентный радиус блока скважин.

Для вертикальной скважины в изотропной среде при наличии однородной прямоугольной сетки D. Peaceman предлагает модель, выраженную в виде:

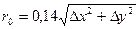. (1.8)

Соответственно в случае анизотропной среды:

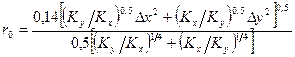. (1.9)

Выражение (1.9) составлено с учетом того, что буровая скважина скорее имеет форму эллипса, чем окружности.

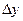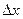По отношению к горизонтальной скважине автор считает достаточным взаимозаменить и , так же как 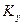и 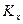в уравнениях (1.7) и (1.9):

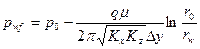; (1.10)

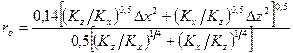. (1.11)

Необходимо учитывать, что уравнения (1.10) и (1.11) основаны на некоторых предположениях. Прежде всего, важны такие факторы, как однородность сетки и проницаемости. Кроме того, предполагается, что скважина изолирована. Под этим подразумевается, что она находится вдали от других скважин и от границ сетки.

Более точный анализ применимости уравнения (1.7) к одиночной горизонтальной скважине дан в работе D. Babu и A. Odeh. Они рассматривают вертикальное поперечное сечение как прямоугольник шириной 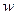и высотой 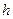при позиции скважины 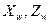, со скоростью потока 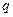. Авторы допускают, что через четыре стороны прямоугольника не проходит поток, и что система находится в псевдоустойчивом состоянии. Тогда дифференциальное уравнение для выражения давления выглядит так:

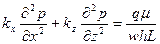. (1.12)

Предполагается, что скважина проходит сквозь всю длину .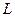

Если допустить, что прямоугольник перекрывается однородной сеткой, имеющей 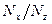блоки величины - 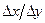, и допустить, что скважина находится в центре блока 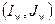, то уравнение (1.12) посредством системы разностей может быть приближено к уравнению:

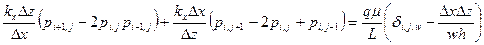. (1.13)

Граничные условия при этом будут:

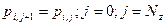; (1.14)

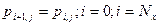. (1.15)

В их работе получено точное решение системы уравнений применительно к данной системе разностей:

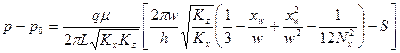, (1.16)

где

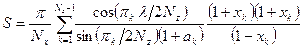; (1.17)

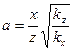; (1.18)

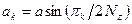; (1.19)

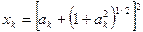; (1.20)

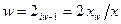; (1.21)

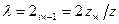. (1.22)

Уравнения (1.16)-(1.22) были проверены по отношению к точным решениям системы разностей и оказались достаточно достоверными.

В изложенных работах рассматривались только равномерные сетки. Тем не менее, где имеется изолированная горизонтальная скважина, предпочтительнее использовать сетку, которая сгущается вблизи скважины, что повышает точность моделирования. D. Peaceman провел ряд экспериментов при изучении влияния сгущения сетки на точность расчетов давления в однородном потоке.

A. Settari и K. Aziz исследовали погрешность метода по отношению к неравномерным сеткам и представили анализ, показывающий, что неравномерные сетки с центрированными блоками должны иметь погрешность порядка 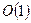. Это означает, что ошибка не должна приближаться к нулю по мере сгущения сетки. Тогда было предложено размещать границы ячеек на половине пути между соседними сеточными узлами. Такое размещение называется сеткой с распределенными узлами [24].

Результаты исследований показывают, что какой бы вид сетки не использовался, способ сгущения вблизи скважины не дает лучшего ответа относительно продуктивности скважины. Однако этот подход часто используется в моделировании горизонтальных скважин.

К настоящему времени наиболее существенными среди научных исследований, посвященным горизонтальным газовым скважинам, являются работы З.С. Алиева и В.В. Шеремета, В.А.Черных. Основная часть работ опубликована в 1995г. В этих работах предложены методы определения забойного давления в горизонтальных газовых скважинах, оборудованных фонтанными трубами, а также в скважинах с большим и со средним радиусом кривизны для перехода ствола от вертикального к горизонтальному положению [1,45,46].

В работах З.С. Алиева и др. в приближенной постановке исследовано влияние толщины пласта, длины и диаметров обсадных колонн и фонтанных труб, устьевого давления, параметра анизотропии, потерь давления по длине ствола на работу горизонтальных скважин, а также степени вскрытия пласта, расположения горизонтального ствола относительно контуров питания. Расчеты показали, что при заданных параметрах вскрываемого пласта и депрессии на пласт дебит горизонтальной скважины снижается при толщинах пласта 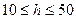м в пределах 2-31% от дебита, полученного при симметричном расположении горизонтального ствола относительно кровли и подошвы.

На примерах полосообразного пласта с различными толщинами и различными значениями радиуса контура питания определено влияние асимметричного расположения горизонтального ствола относительно контуров питания на производительность газовой скважины. Из этих расчетов следует, что при расположении горизонтального ствола у контура питания производительность скважины за счет асимметрии по R_k существенно снижается и составляет 52,0-70,3% от дебита, получаемого при симметричном расположении ствола. Получено приближенное решение задачи, одновременно учитывающее асимметричное расположение горизонтального ствола по толщине и относительно контуров питания.

Одной из заслуживающих внимания является работа З.С. Алиева, В.В. Шеремета [1], посвященная определению производительности горизонтальных скважин, вскрывших газовые и газонефтяные пласты. В этой работе обоснованы технологические режимы эксплуатации горизонтальных скважин при вскрытии устойчивых и неустойчивых коллекторов, при наличии подошвенной воды, с учетом нелинейности закона фильтрации для газовой фазы, неоднородности пласта, расположения и конструкции скважин, гравитационных и капиллярных сил, а также изменения свойств газа, нефти и воды от давления. Приведены результаты практических расчетов или универсальные зависимости для практического использования.

М.В. Колонтай и В.С. Путохин приводят решение для нефтяной скважины сложного профиля, в котором используется численная модель трехмерной трехфазной фильтрации с учетом гидравлических сопротивлений по стволу скважины. Однако численная модель требует разбиения пласта на блоки и усреднения давления в блоках. Не определены дебиты отдельных перфорационных отверстий, а так же местные гидравлические сопротивления перфорационных отверстий в стволе скважины. Не учитывается интерференция перфорационных отверстий в пласте и др. [28]

В работе [30] дано решение для строго горизонтальной нефтяной скважины с открытым забоем с учетом распределения давления по стволу скважины. Однако для притока к элементарному участку горизонтального ствола они использовали формула Дюпюи для вертикальной скважины. Влияние границ пласта не учитывалось. Сделан вывод о существовании предельной длины горизонтального ствола для заданной депрессии.

В работе Б.М. Сучкова рассматривается повышение производительности скважин методом кавернообразования. Эффективность метода не подлежит сомнению. Его можно применять для интенсификации добычи нефти в горизонтальных скважинах. Учитывая достаточно большую протяженность горизонтальной части ствола скважины, каверны могут быть образованы в различных интервалах. При этом должны быть соблюдены определенные требования как по выбору мест каверно­образования, так и последовательности обработки. Наилучшие резуль­таты данный метод дает при поинтервальной дифференциации зон притока жидкости с учетом процентного соотношения нефти и воды, характера об­воднения, химического состава и плотно­сти воды и др. Последовательность кавернообразования может также зависеть от системы разработки с использованием закачки воды в пласт. Так, например, образование каверн-накопителей в горизон­тальной части стягивающего ряда рекомендуется проводить после­довательно в середине и начале ствола, а затем между соседними интервалами на равном удалении. После снижения производительности скважин до предыдущей первоначальной величины создают новую каверну­-накопитель. В результате образуется равномерная обработка участ­ков горизонтального ствола, способствующая выравниванию фронта вытеснения и увеличению нефтеотдачи пласта. Метод последова­тельного равномерного формирования каверн-накопителей может быть использован и при отсутствии существенных отличий прони­цаемости пород по открытому стволу скважины, а также при недос­таточной информации о поинтервальных притоках вдоль ствола скважины. При наличии же такой информации выбор мест образова­ния каверн-накопителей устанавливается более точно [74].

Использование этого метода дает возможность оптимизировать приток жидкости по всему горизонтальному участку ствола скважи­ны. Участки горизонтального ствола, близко расположенные к газо­носным зонам, зонам водопритоков, а также подошвенным водам, исключаются для какого-либо воздействия кислотных растворов.

Основные усилия исследователей за рубежом в настоящее время направлены на создание цифровых моделей, учитывающих влияние перфорации, гидравлических сопротивлений ствола, профиля ствола скважины и т.д. Ввиду большой сложности моделей, исследования направлены на повышение эффективности их работы, но результаты расчетов по ним пока не известны. Аналитические модели, предлагаемые нами более просты, но позволяют на этапе технико-экономического обоснования разработки месторождений обосновать конструкцию стволов пологих скважин и оценить их продуктивность.

К малоизученным вопросам до настоящего времени относились: влияние профиля ствола скважины на производительность пологих скважин, расположения участков перфорации и фильтров по длине ствола и всех видов гидравлических сопротивлений в стволе.

К неизученным вопросам для многоствольных скважин так же относятся: взаимовлияние стволов; влияние на профиль притока гидравлических сопротивлений в стволах; влияние на профиль притока расположения интервалов перфорации и фильтров и другие.