Сложность задач дискретной оптимизации

В рамках современной теории сложности сложились различные направления, одно из этих направлений связано с постановкой вопроса, существуют ли эффективные алгоритмы решения переборных (или комбинаторных) задач.

В теории сложности используется понятие вычислительной сложности, дадим здесь предварительное определение этого понятия.

Число шагов (или элементарных операций) алгоритма 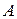, необходимых для нахождения решения некоторой задачи 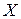, определяет временну́ю вычислительную сложность алгоритма 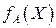. Легкорешаемые задачи имеют полиномиальную временну́ю сложность, а сложность трудно решаемых задач экспоненциальна.

Замечание. В настоящее время помимо чисто полиномиальных и экспоненциальных алгоритмов иногда используются алгоритмы, сложность которых ни полиномиальна, ни экспоненциальна, так, согласно [1], скорости роста, такие как 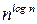, которые превосходят любой полином, но меньше, чем 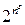, , 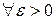называются иногда субэкспоненциальными. Ниже будем пользоваться понятием квазиэкспоненциальных алгоритмов со скоростью роста сложности .

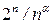В настоящее время показано, что существуют универсальные переборные задачи – задачи, из полиномиальной разрешимости которых следует полино­миальная разрешимость любой переборной задачи. Таких универсальных задач сейчас известно несколько тысяч (среди них хорошо известные задача комми­вояжера, задача о раскраске, задача о покрытии, многие задачи теории расписаний).

Известна гипотеза, что для универсальных задач вообще не существует эффективных методов решения переборных задач.

Можно выделить такие типы комбинаторных задач как оптимизационные задачи и задачи распознавания свойств (можно привести пример последней задачи: ответить на вопрос, существует ли допустимое решение 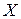, такое, что значение целевой функции для него не менее 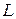). При этом особо выделяются классы задач: 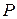– класс задач распознавания, которые могут быть решены некоторым полиномиальным алгоритмом, класс NP содержит индивидуальные задачи 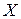, для которых в случае ответа «да» существовало бы удостоверение полиномиальной длины для 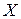. Понятно, что 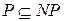, известная проблема « 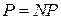?» является одним из наиболее важных теоретических вопросов в теории сложности.

Мы же в дальнейшем будем интересоваться такими характеристиками сложности алгоритмов, которые позволяли бы сравнивать известные алгоритмы между собой. Остановимся на некоторых из этих характеристик.

Под вычислительной сложностью алгоритма, как отмечено выше, понимают количество условных шагов или операций, необходимых для решения задачи. Одним из наиболее распространенных методов оценки трудоемкости алгоритмов является экспериментальный метод, основанный на многократном решении задач различных размерностей и эмпирической оценке интересующих величин и зависимостей. Однако этот подход имеет существенный недостаток – он не дает достаточной уверенности в том, что результаты машинного эксперимента достигаются и на множестве данных, отличных от исследованных. В [6] отмечено: «…чтобы быть практически полезной, информация о сложности алгоритма должна быть машинно-независимой». В связи с этим широко распространен подход, использующий некоторую модель вычислительного устройства, применяемого для реализации алгоритма. В качестве вычислительных устройств обычно используются машина с производным доступом к памяти и хранимой программой или машина Тьюринга.

При введении оценок сложности алгоритмов решения комбинаторных задач обычно различаются индивидуальная задача и массовая задача (или прос­то задача), последняя представляет собой множество индивидуальных задач. При этом для оценки трудоемкости алгоритмов используются следу­ющие характеристики: временнáя вычислительная сложность алгоритма – время, за­трачиваемое алгоритмом для решения задачи, емкостная сложность алго­ритма – объем памяти, необходимый для реализации алгоритма. Для сгла­жи­вания резких различий в поведении алгоритма при переходе от одной инди­ви­дуальной задачи к другой, можно рассматривать все индивидуальные задачи од­ной размерности 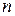вместе и определить сложность алгоритма для этой раз­мерности задачи как число шагов (или условных операций) алгоритма в худ­шем случае, т. е. находится временнáя вычислительная сложность 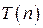в предположении, что для данного алгоритма входные данные задачи явля­ются наихудшими из возможных, другими словами, находится верхняя оценка сложности алгоритма, говорящая о том, что данный алгоритм решает задачу не более чем за 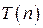условных единиц времени. Если для некоторого алгоритма верхняя оценка сложности меньше, чем для других алгоритмов, то говорят, что этот алгоритм имеет характеристику «в худшем случае» лучше, чем другие алгоритмы.

Ориентация на худший случай иногда приводит к пессимистическим прогнозам поведения алгоритмов, так, хорошо известный симплекс-алгоритм на практике работает как полиномиальный алгоритм (это же показывает и теоретический анализ его поведения «в среднем»), хотя оценка сложности в худшем случае для него является экспоненциальной[7].

В связи с этим с практической точки зрения часто бóльший интерес представляет средняя оценка вычислительной сложности[8], позволяющая судить о поведении алгоритма в среднем на некотором классе задач, однако средняя оценка вычислительной сложности тоже не дает полной характеристики эффективности алгоритма, так как возможны задачи, при решении которых сложность алгоритма превысит эту оценку.

Важной характеристикой алгоритма является асимптотическая оценка слож­ности – порядок скорости роста сложности алгоритма при увеличении размерности задачи. Асимптотические оценки вычислительной сложности ал­горитмов позволяют судить об их поведении при решении задач большой раз­мерности и определить границы применимости алгоритма, более того, «…имен­но асимптотическая сложность алгоритма определяет в итоге размер за­дач, которые можно решить этим алгоритмом» [1, с. 12]. Важность изучения асимптотических оценок вычислительной сложности алгоритмов об­условлена также ускоренным ростом быстродействия современной вычис­ли­тель­ной техники и необходимостью решения задач большой размерности. Срав­нивая алгоритмы по асимптотическим оценкам сложности, следует иметь в виду, что вычислительная сложность алгоритма может харак­теризоваться бóльшим порядком скорости роста, но характеризоваться мень­шей мульти­пликативной константой, чем другой алгоритм. В этом случае, алго­ритм, харак­теризующийся большой скоростью роста сложности, может оказаться эффек­тивнее других алгоритмов для решения задач небольшой размерности.