Лекция № 12. УРАВНЕНИЕ ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ ДЛЯ ПОТОКА. ИСТЕЧЕНИЕ ГАЗОВ И ПАРОВ. ДРОССЕЛИРОВАНИЕ.

Под открытыми термодинамическими системами понимаются термодинамические системы, которые кроме обмена теплотой и работой с окружающей средой допускают обмен массой. В технике широко используются процессы преобразования энергии в потоке, когда рабочее тело перемещается из области с одними параметрами (p₁ v₁) в область с другими параметрами (p₂ v₂). Это, например, расширение пара в турбинах, сжатие газа в компрессорах.

Рассмотрим одномерные стационарные потоки, в которых параметры зависят только от одной координаты, совпадающей с направлением вектора скорости, и не зависящей от времени. Условие неразрывности течения в таких потоках заключается в одинаковости массового расхода m рабочего тела в любом его сечении.

m = Fc/v= const

Где F – площадь поперечного сечения канала

с– скорость рабочего тела.

Рассмотрим открытую термодинамическую систему, представленную на рисунке

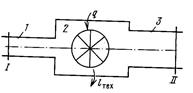
По трубопроводу 1 рабочее тело с параметрами Т₁ v₁p₁ подаётся со скоростью с₁ в тепломеханический агрегат 2 (двигатель, паровой котёл, компрессор и т.д.) Здесь каждый килограмм рпабочего тела в общем случае может получить от внешнего источника теплоту q и совершить техническую работу l_тех например, приводя в движение ротор турбины, а затем удаляется через выхлопной патрубок 3 со скоростью с₂, имея уже параметры Т₂ v₂p₂

Если в потоке мысленно выделить замкнутый объём рабочего тела и наблюдать за изменением его параметров в процессе перемещения, то для описания его поведения будут пригодны все полученные ранее термодинамические соотношения, в том числе первый закон термодинамики, который можно записать в обычной его форме

q = ∆u + l

Внутренняя энергия есть функция состояния рабочего тела, поэтому значение u₁ определяется параметрами рабочего тела при входе (сечение потока 1), а значение u₂ – параметрами рабочего тела при выходе из агрегата ( сечение 2).

Работа расширения совершается рабочим телом на поверхностях, ограничивающих выделенный движущийся объём, т.е. на стенках агрегата и границах выделяющих этот объём в потоке. Часть стенок агрегата неподвижна, и работа расширения на них равна нулю. Другая часть стенок специально делается подвижной (рабочие лопатки в турбине и компрессоре, поршень в поршневой машине), и рабочее тело совершает на них техническую работу l_тех.

При входе рабочее тело вталкивается в агрегат. Для этого необходимо преодолеть давление р_1. Поскольку р₁ = const, то каждый килограмм рабочего тела может занять объём v₁ лишь при затрате работы, равной l_вталк = - v₁p₁

Для того, чтобы выйти в трубопровод 3, рабочее тело должно вытолкнуть из него такое же количество рабочего тела, ранее находившегося в нём, преодолев давление р₂ т.е., каждый килограмм занимая объём v₂, должен произвести определённую работу выталкивания l_выталк = v₂p₂

Сумма l_в = р₂v₂ - р₁v₁ называется работой вытеснения. Если скорость с₂ на выходе больше скорости с₁ на вхъоде6, то часть работы расширения будет затрачена на увеличение кинетической энергии рабочего тела в потоке, равное с₂²/2 – с₁²/2

Наконец, в неравновесном процессе, некоторая работа l_тр может быть затрачена на преодоление сил трения. И окончательно работа определится выражением

l = l_тех. + (р₂v₂ - р₁v₁) + (с₂²/2 – с₁²/2) + l_тр

Теплота, сообщаемая каждому килограмму рабочего тела во время прохождения его через агрегат, складывается из теплоты внешней q_внеш, подведённой снаружи и теплоты q_тр, в которую переходит работа трения внутри агрегата т.е.

q = q_внеш + q_тр

Подставив полученные значения работы и теплоты в уравнение первого закона термодинамики, получим

q_внеш + q_тр = u₂ - u₁ + l_тех. + (р₂v₂ - р₁v₁) + (с₂²/2 – с₁²/2) + l_тр

Поскольку теплота трения равна работе трения(q_тр = l_тр), а u + рv = h, окончательно можно записать

q_внеш = h₂ - h₁ + l_тех + (с₂² – с₁²)/2

Данное выражение является уравнением первого закона термодинамики для потока, которое можно сформулировать так – теплота, подведённая к рабочему телу извне, расходуется на увеличение энтальпии рабочего тела, производство технической работы и увеличение кинетической энергии потока.

Тепловой двигатель

(с₂² – с₁²) < l_тех. q_внеш, =0, поэтому рабочее тело пролизводит техническую работу за счёт уменьшения энтальпии.

l_тех = h₁ - h₂

h₁ - h₂ –располагаемый теплоперепад

Компрессор.Если процесс сжатия газа происходит без теплообмена с окружающей средой (это обеспечивается надлежащим выбором сечений всасывающего и нагнетательного воздухопроводов), то

l_тех = h₁ - h₂

В отличие от теплового двигателя здесь h₁ >h₂, т.е. техническая работа в адиабатном компрессоре затрачивается на увеличение энтальпии газа.

Сопла и диффузорыСпециально спрофилированные каналы для разгона рабочей среды и придания потоку определённого направления называются соплами. Каналы, предназначенные для торможения потока и повышения давления, называются диффузорами.Техническая работа в них не совершается, поэтому

dq_внеш = dh + dq_внеш = dh + d(с²/2)

Однако, если рабочее тело движется в потоке без трения, то первый закон термодинамики для закрытой системы

dq_внеш = dh - ndp

Приравняв правые части двух последних уравнений получим

сdс = - ndp

Из этого уравнения видно, что dс и dp всегда имеют противоположные знаки. Следовательно, увеличение скорости течения в потоке возможно лишь при уменьшении в нём давления. Наоборот, торможение потока сопровождается увеличением давления.

Так как длина сопла и диффузора невелика, а скорость течения среды в них достаточно высока, то теплообмен в них между стенками канала и средой при малом времени их контакта настолько незначителен, что в большинстве случаев им можно пренебречь и считать процесс истечения адиабатным (q_внеш = 0)

При этом, уравнение первого закона термодинамики для потока примет вид

(с₂² – с₁²)\2 = h₁ - h₂

Следовательно ускорение адиабатного потока происходит за счёт уменьшения энтальпии, а торможение потока вызывает её увеличение, т.е. располагаемая работа при адиабатном расширении равна располагаемому теплоперепаду.

При решении задач, связанных с истечением газа или пара через сопла (насадки), чаще всего приходится определять скорость истечения и расход, т.е. количество газа или пара, вытекающего в единицу времени.

Рисунок 12.1 – Истечение газа или пара через сопло

В этих случаях необходимо прежде всего найти отношение , где р₂ – давление среды на выходе из сопла; р₁ – давление среды на входе в сопло.

Полученное числовое значение 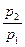сравнивают с критическим отношением давлений для данного газа.

Для одноатомных газов ( 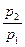)_кр=0,487;

Для двухатомных газов ( 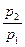)_кр=0,528; для трёх- и многоатомных газов ( 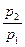)_кр=0,546.

1) Если адиабатное истечение газа происходит при 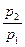>( 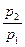)_кр, то теоретическая скорость газа у устья суживающегося сопла определяется по формуле

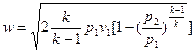, (1)

где 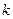- показатель адиабаты;

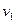- удельный объём газа на входе в сопло.

Для идеального газа теоретическая скорость, м/с, определяется по формуле

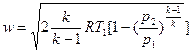, (2)

В формулах (1) и (2) значения p, v, R даны соответственно в следующих единицах: Па, кг/м³, Дж/(кг∙К).

Теоретическая скорость газа, м/с, может быть найдена

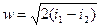, (3)

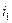где и 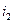- соответственно энтальпии газа в начальном и конечном состояниях, Дж/кг.

Расход газа определяется по формуле

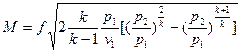, (4)

где 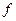- выходное сечение сопла, м².

2) Если адиабатное истечение газа происходит при 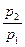≤( 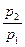)_кр, то теоретическая скорость газа у устья суживающегося сопла будет равна критической скорости и определяется по формуле

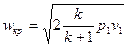(5)

Для двухатомных газов критическая скорость определится

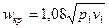(6)

или

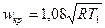(7)

Критическая скорость газа, м/с, может быть найдена

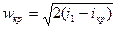, (8)

где 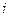- энтальпия газа при критическом давлении р_кр , Дж/кг.

Расход газа в этом случае будет максимальным и определится

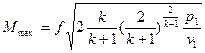, (9)

Для двухатомных газов

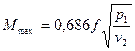, (10)

Для трёхатомных газов

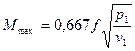, (11)

Для получения скоростей истечения выше критических (сверхзвуковые скорости) применяется расширяющееся сопло, или сопло Лаваля (рисунок 2) в минимальном сечении сопла Лаваля скорость движения газа равна критической скорости или скорости звука, определяемой параметрами р_кр и v_кр.

Рисунок 12.2 – Сопло Лаваля

Площадь минимального сечения сопла определяется по формуле

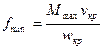(12)

Для двухатомных газов

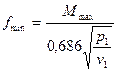(13)

Для трёхатомных газов

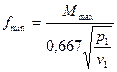(14)

Площадь выходного сечения сопла

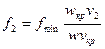, (15)

где 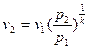- удельный объём газа при давлении среды р₂.

Длина расширяющейся части сопла 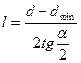, (16)

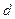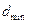где и - соответственно диаметры входного и минимального сечений;

Α – угол конусности расширяющейся части сопла.

Площадь поперечного сечения определяется по формуле

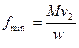(17)