Скорость фильтрации, Линейный закон Дарси.
В теории фильтрации движение жидкости или газа через пористую среду рассматривается не с точки зрения движения потоков по отдельным извилистым микроскопическим каналам, а распространяют расход жидкости или газа на всю поперечную площадь пористой среды. Эта фиктивная скорость называется скоростью фильтрации. Истинные скорости движения в отдельных каналах могут значительно превышать скорость фильтрации. В связи с этим все законы фильтрации, устанавливающие связь между скоростью фильтрации, градиентом давления и параметрами пористой среды и жидкости, носят статический характер.
При изучении фильтрационного потока удобно отойти от размеров пор и их формы, допустив, что жидкость движется сплошной массой, заполняя весь объем пористой среды, включая пространство, занятое скелетом породы.
Скорость фильтрации в пределах площадки можно выразить в виде
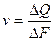 . (3)
. (3)
Скорость фильтрации в данной точке пласта
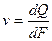 , (4)
, (4)
где 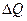 - объемный расход жидкости в единицу времени через площадку
- объемный расход жидкости в единицу времени через площадку 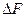 .
.
Установим связь между скоростью фильтрации и средней скоростью движения жидкости в порах
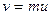 , (5)
, (5)
где 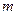 - коэффициент пористости.
- коэффициент пористости.
Скорость фильтрации можно рассматривать как вектор. Если в данной точке области фильтрации вращать элементарную площадку и восстанавливать нормали, соответствующее наибольшему расходу, будет направлением вектора скорости фильтрации.
В средине прошлого столетия в результате экспериментального изучения движения воды через песчаные фильтры был установлен основной закон фильтрации – закон Дарси (или линейный закон фильтрации). Этот закон является хронологически первым законом теории фильтрации. Его можно записать в виде
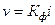 , (6)
, (6)
где 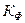 - коэффициент фильтрации, имеющий размерность скорости;
- коэффициент фильтрации, имеющий размерность скорости;
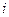 - гидравлический уклон.
- гидравлический уклон.
Коэффициент фильтрации зависит от свойств пористой среды и свойств фильтрующееся жидкости. Наибольшее влияние на этот коэффициент оказывают размеры частиц породы. Величина этого коэффициента также зависит от формы частиц, степени шероховатости их поверхности, пористости среды, вязкости жидкости.
Видоизменив формулу (6) перейдем к виду
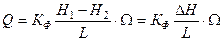 , (7)
, (7)
где 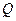 - объемный расход жидкости;
- объемный расход жидкости; 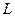 - длина участка фильтрации;
- длина участка фильтрации; 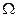 - площадь фильтрационной поверхности;
- площадь фильтрационной поверхности; 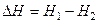 - разность напоров воды.
- разность напоров воды.
Таким образом, закон Дарси заключается в том, что скорость фильтрации пропорциональна градиенту давления.
Закон Дарси имеет силу, если соблюдаются следующие условия:
1) мелкозернистая пористая среда или достаточно узкие поровые каналы;
2) малая скорость фильтрации при небольшом градиенте давления;
3) незначительные изменения скорости фильтрации или градиета давления.
Закон Дарси, в дифференциальной форме он имеет вид:
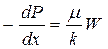 , (8)
, (8)
где 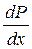 - градиент давления (сил трения), W – скорость фильтрации, m - коэффициент динамической вязкости, k – коэффициент проницаемости.
- градиент давления (сил трения), W – скорость фильтрации, m - коэффициент динамической вязкости, k – коэффициент проницаемости.
Знак (-) в левой части формулы (8) означает, что течение газа происходит в направлении, противоположном росту давления.
Фундаментальный закон фильтрации (8) устанавливает связь между скоростью фильтрации и градиентом давления.
3. Нелинейные законы фильтрации
Проведенные в дальнейшем эксперименты показали, что закон Дарси не является универсальным и нарушаются области малых и больших скоростей. Нарушение в области малых скоростей связано с молекулярным эффектом. Причины, вызывающие отклонение от закона Дарси при больших скоростях, являются до настоящего времени предметом дискуссии среди исследователей.
В 1901 году Форхгейме, ссылаясь на исследования Мазони, рекомендовал выражать зависимость градиента давления от скорости двучленным законом фильтрации:
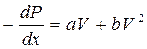 , (9)
, (9)
Двучленный закон фильтрации в дифференциальной форме при прямолинейной фильтрации газа в принятых сейчас обозначениях, без учета силы тяжести имеет два вида записи:
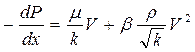 , (10)
, (10)
или
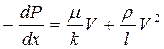 (11)
(11)
где b - дополнительная константа пористой среды, определяемая экспериментально, l – коэффициент макрошероховатости, характеризующий структуру порового пространства, r - плотность газа (жидкости).
Первое слагаемое в правой части уравнения (10) учитывает потери давления вследствие вязкости жидкости, второе слагаемое – инерционную составляющую сопротивления движению жидкости, связанную с криволинейностью и извилистостью поровых каналов.
При малых скоростях течения природа нелинейности закона фильтрации иная. Чем в области больших скоростей фильтрации (больших значений числа Рейнольдса). Она связана с проявлением неньютоновских свойств фильтрующихся флюидов, а также других Физико-химических эффектов. Поэтому для качественного изучения вопроса и количественной оценки этих эффектов необходимо отказаться от модели вязкой однородной жидкости и заменить ее какой-либо другой реологической моделью пластового флюида.
Ограничимся формулировкой наиболее простого нелинейного закона фильтрации неньтоновских жидкостей, в основе которого лежит модель фильтрации с предельным градиентом. Для случая одномерного линейного потока его можно представить в виде
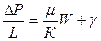 , (
, ( 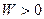 ),
),
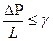 ,
, 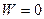 ,
,
где 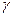 - предельный (начальный) градиент давления, по достижении которого начинается движение жидкости: при меньших значениях градиента движения отсутствует, этот параметр измеряется в лабораторных условиях.
- предельный (начальный) градиент давления, по достижении которого начинается движение жидкости: при меньших значениях градиента движения отсутствует, этот параметр измеряется в лабораторных условиях.
Закон фильтрации записывают также в виде одночленной степенной формулы:
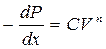 (12)
(12)
где С и n - постоянные, определяемые опытным путем, причем 1< n < 2.
При n = 1 из (12) получается закон Дарси, при n = 2 – квадратичный закон А.А. Краснопольского.
Таким образом, формула (10) имеет два параметра b и k, которые подлежат дальнейшему изучению и установлению связи между ними.
Входящий в линейный закон фильтрации Дарси (8) коэффициент проницаемости определяется при исследовании кернов или на основе гидродинамических исследований.
Исследованиями показано, что для пористых сред коэффициент проницаемости зависти от размера зерен и их дисперсности, коэффициента пористости, формы зерен, степени их сцементированности и. т. д.
Л. С. Лейбензон предложил выразить коэффициент проницаемости в виде:
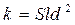 (13)
(13)
где d – линейный размер (диаметр) зерен пористой среды, Sl – безразмерный критерий (число Слихтера), зависящий от коэффициента пористости и структуры порового пространства, т. е.
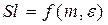 (14)
(14)
где e - некоторый параметр, характеризующий структуру порового пространства пласта, m – коэффициент пористости.
4. Границы применимости закона Дарси.
Верхняя граница определяется группой причин связанных с проявлением инерционных сил при высоких скоростях фильтрации. Верхнюю границу применимости закона Дарси связывают обычно с некоторым критическим (предельным) значением Re кр числа Рейнольдса:
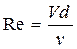 ,
, 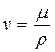 , (15)
, (15)
где - d – линейный размер пористой среды, v - кинематический коэффициент вязкости флюида.
Экспериментальные исследования Льюиса, Фэнчера, Линквиста показали зависимость коэффициента гидравлического сопротивления от числа Рейнольдса.
Таблица 1
Определение верхней границы применимости закона Дарси по данным различных авторов
| Автор | 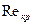
|
| Н. Н. Павловский | 7,5-9 |
| Фенчер, Льюис, Бернс | 1-4 |
| М. Д. Миллионщиков | 0,022-0,29 |
| Ф. И. Котяхов (Г. Ф. Требин) | 0,3 |
| В. Н. Щелкачев | 1-12 |
| А. И. Абдулвагабов | 0,019-8,1 |
Интервалы критических значений Re для различных образцов пористых сред
Таблица 2
| Образец пористой среды | Диапазон критических значений |
| Однородная дробь | 13-14 |
| Однородный крупнозернистый песок | 3-10 |
| Неоднородный мелкозернистый песок с преобладанием фракций диаметром менее 0,1 мм | 0,34-0,24 |
| Сцементированный песчаник | 0,05-1,4 |
Однако вследствие различной структуры и состава пористых сред получить такую универсальную зависимость не удается.
Первая количественная оценка верхней границы применимости закона Дарси была выполнена Павловским, который, опираясь на результаты Слихтера, полученные для модели идеального грунта, и полагая характерный размер d равный эффективному диаметру d эф вывел следующую формулу для числа Рейнольдса:
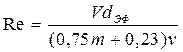 , (16)
, (16)
Использовав эту формулу и данные экспериментов, Н. Н. Павловский установи, что критическое значение числа Рейнольдса находится в пределах
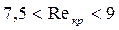 .
.
Достаточно узкий диапазон изменения значений 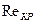 объясняется тем, что в опытах использовались не слишком разнообразные образцы пористых сред.
объясняется тем, что в опытах использовались не слишком разнообразные образцы пористых сред.
Для удобства обработки результатов многочисленных экспериментов различных авторов В.Н.Щелкачев предложил использовать безразмерный параметр, названный им параметром Дарси
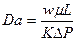 . (17)
. (17)
Отсюда видно, что параметр Дарси представляет собой отношение силы вязкого трения к силе давления. Из выражения (17) следует, что если параметр Дарси равен единицы
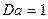 , (18)
, (18)
то закон Дарси справедлив.
Таким образом, равенство (18) должно выполняться при 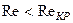 . Данный параметр упрощает исследование границы применимости линейного закона фильтрации.
. Данный параметр упрощает исследование границы применимости линейного закона фильтрации.
Нижняя граница определяется проявлением неньютоновских реологических свойств жидкости, ее взаимодействия с твердым скелетом пористой среды при достаточно малых скоростях фильтрации.
Ограничимся формулировкой наиболее простого нелинейного закона фильтрации неньютоновских жидкостей, в основе которого лежит модель фильтрации с предельным градиетом. Для случая одномерного линейного потока его можно представить в виде
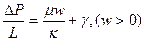 (19)
(19)
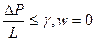 ,
,
Лекция 2
Дата добавления: 2017-04-05; просмотров: 8190;










