Математические модели агломерационного процесса
Производительность агломашины и качество агломерата связаны с целым рядом независимых переменных величин процесса. Так как эти связи весьма сложны и еще недостаточно изучены, в настоящее время удается установить аналитические соотношения только между некоторыми параметрами процесса.
Режим спекания агломерата зависит от следующих независимых переменных: содержание углерода в шихте С; влажность шихты W;высота слоя шихты на ленте Н; вакуум на всасе? эксгаустера р0;коэффициент положения заслонок в вакуум-камерах k (α).
Подача возврата в шихту b и в постель а влияет на тепловой режим, но в то же время и является следствием хода процесса. Это же относится и к скорости фильтрации воздуха через слой шихты на ленте g, характеризующей вертикальную скорость спекания wh.
Производительность аглоленты может быть записана в следующем виде:
Маc = Ма + Мв + Мп, (5)
где Маc - массовый расход аглоспека, т/ч; Ма - массовый расход годного агломерата, т/ч; Мв - массовый расход возврата, т/ч; Мп - массовый расход постели, т/ч.
Тогда
b = Мв/Мас, а = Мп/Мас.
Если обозначить через φ долю вводимого в шихту возврата, то
φ = Мв/(Мв + Мш), (6)
где Мш - массовый расход шихты, т/ч.
Между φ и b существует практически линейная зависимость
φ = k1b>, (7)
где k1 - коэффициент.
Вакуум в камерах разрежения p зависит от р0, k (α) и g:
р = р0 - k (α) g2. (8)
Удельная производительность аглоленты т равна
т = ρш wh ki kг, (9)
где ρш - средняя насыпная плотность шихты; wh - вертикальная скорость спекания;
ki - выход аглоспека из шихты по сравнению с массой уложенной шихты с учетом выделения летучих компонентов при спекании; kг - выход годного из аглоспека, равный kг = Ма/Мас = 1 - b - a;
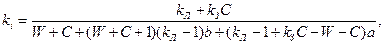
где kл - коэффициент потери летучих компонентов, включая и пылеунос; kз– коэффициент зольности топлива.
Существенной частью работы АСУ ТП аглофабрики является реализация алгоритма расчета аглошихты. Введем обозначения: Mj - масса компонентов шихты (концентрата, руды, известняка, доломита, возврата, топлива и др.); Fea, MgOa, Раи др. - содержание химических составляющих в агломерате; Fe3a, MgO3a, Р3a и др. - то же, заданные значения; Fej, MgOj, Рj - и др. - содержание химических составляющих в шихтовых материалах; Фа = CaOa/SiО2a - основность агломерата; Wj, ρj - влажность и потери при агломерации каждого компонента шихты; αj - доля j-того компонента в шихте.
Уравнение материального баланса в этих обозначениях принимают вид:
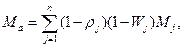 (10)
(10)
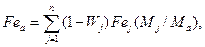 (11)
(11)
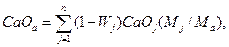 (12)
(12)
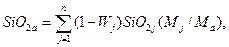 (13)
(13)
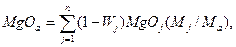 (14)
(14)
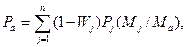 (15)
(15)
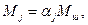
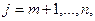 (16)
(16)
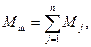 (17)
(17)
где Мш - масса шихты; n - количество материалов, используемых для составления шихты; т - та часть из них, которая выбирается независимо от общего веса шихты; {т + 1,. . . , п) - часть материалов, которая дозируется в процентах от общей массы шихты (известь, топливо, возврат).
Задача расчета шихты состоит в выборе таких величин Mj, j = 1, 2 ,..., п, которые обеспечивают заданные показатели агломерата:
Мш= Мш, (18)
Fea = Fea, (19)
Фа = Фа, (20)
MgOa = MgOa, (21)
Pa ≤ Paдоп (22)
где Радоп - допустимое содержание фосфора в агломерате.
Расходы компонентов шихты неотрицательны и ограничены, т.е.
Мj ≥ 0, j = 1,2, ...,n, (23)
Мj ≤ Мjmax, j = 1,2, ...,n. (24)
Возможны ограничения на соотношения компонентов, которые могут быть представлены выражениями вида
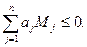 . (25)
. (25)
Шихтовка - набор величин Mj, j = 1, 2 ,..., п, - находится как решение системы равенств и неравенств (10) - (25).
В принципе указанная система может не иметь решения. В таком случае для учета реальных возможностей управления химическим составом агломерата необходимо ослабить требования. Чаще всего отказываются от требования стабилизации содержания железа, для этого вместо (19) вводят условие
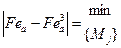 . (26)
. (26)
В такой постановке задача шихтовки становится задачей нелинейного программирования.
Таким образом, общая картина декомпозиции математического описания агломерационного процесса имеет вид иерархической структуры.
Декомпозиция математического описания исходной системы сводится к выделению отдельных агрегатов (уровень I), в рамках которых затем выделяются отдельные узлы и части конструкций (уровень II). Далее в отдельных узлах выделяются простейшие физические элементы (уровень III) и, наконец, к ним-то и «подбираются» известные уравнения математической физики. (Подчеркнем, что уравнения математической физики записаны для процессов, протекающих в идеализированных условиях.)
Таким образом, математическое описание объекта как таковое появляется лишь на самом последнем уровне декомпозиции (уровень IV), который будем определять как уровень элементарных физических процессов. Подобным же путем составляются математические модели для всех узлов, агрегатов и установок агломерационного процесса, а также и любых других технологических процессов. После добавления и согласования взаимосвязей между изучаемыми процессами IV, элементами III, узлами II, агрегатами I получаем исходную математическую модель всей изучаемой системы.
Основная литература
1. Математическое моделирование управляющих систем: Учебное пособие. — М.: Изд-во РУДН, 2003. — 80 с.
Дата добавления: 2017-04-05; просмотров: 1907;











