Интенсивность источника тепла при прохождении через раствор электрического тока
Основным источником тепла в электрохимических аппаратах является тепло Джоуля-Ленца, которое выделяется при прохождении через раствор электрического тока. Тепло Джоуля-Ленца определяется величиной тока (I) и значением греющего напряжения на электролизере (Uгр):
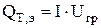 , Дж/с (4.20)
, Дж/с (4.20)
Греющее напряжение отличается от общего напряжения (U) на электролизере, которое может быть измерено, на величины теплового э.д.с. разложения (ER,T) и падения напряжения в контактах (DUK):
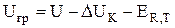 , В (4.21)
, В (4.21)
При расчете греющего напряжения тепловое э.д.с. разложения исключается из напряжения на ванне:
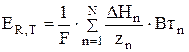 , (4.22)
, (4.22)
где N - количество параллельно протекающих электрохимических реакций; DHn - изменение энтальпии в процессе n-ой электрохимической реакции; zn, Втn - число электронов и выход по току n-ой реакции, соответственно.
Изменение энтальпии определяется как разница энтальпий (DHn,i) продуктов реакции (стехиометрический коэффициент продуктов реакции nj>0) и исходных веществ (nj<0) (i=1...L, L - количество компонентов, участвующих в n-ой электрохимической реакции):
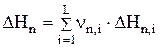 (4.23)
(4.23)
Падение напряжения в контактах, расположенных вне электрохимического аппарата над электролитом, также не вызывает разогрева электролита (ур. 4.21). Однако при расчете теплового баланса ванн барабанного и колокольного типов, в которых контакты находятся под слоем электролита, тепло, образующееся от разогрева контактов, приводит к разогреву электролита. В этом случае при расчете греющего напряжения DUK не вычитают из общего напряжения на электролизере:
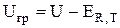 . (4.24)
. (4.24)
4.2.3. Источники тепла за счет явлений переноса
За счет различных явлений переноса тепла электролит может охлаждаться или нагреваться в зависимости от соотношения температуры электролита и температуры окружающей среды.
Передача тепла может осуществляться по механизмам конвекции, теплопроводности, излучением, и в процессе массопереноса. Передача тепла осуществляется через разные участки электролизера: с зеркала электролита по механизму конвекции и излучения; при выделении на электродах газообразных продуктов - по механизму массопереноса; через стенки и дно электролизера - совместная теплопередача теплопроводностью, конвекцией и излучением.
Количество тепла, передаваемое излучением (с зеркала электролита, от стенки или дна ванны) в единицу времени, определяется уравнением:
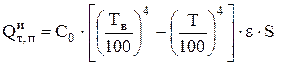 , Дж/с или Вт (4.25)
, Дж/с или Вт (4.25)
С0 =5,68 Вт/м2/град4 - коэффициент излучения абсолютно черного тела;
e - степень черноты излучающей поверхности [22];
Т - температура теплоотдающей поверхности электролизера (электролит, стенка или дно), 0К;
Тв - температура окружающей среды, 0К;
S - площадь отдающей поверхности, м2.
Из уравнения (4.25) видно, что если температура электролита выше температуры окружающей среды, то интенсивность 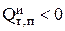 , то есть излучение тепла приводит к охлаждению электролита.
, то есть излучение тепла приводит к охлаждению электролита.
Скорость передачи тепла по механизму конвекции определяется по уравнению:
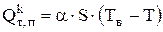 , Вт или Дж/с , (4.26)
, Вт или Дж/с , (4.26)
где a - коэффициент теплоотдачи, Вт/(м2×град).
Для расчета коэффициента теплоотдачи при свободной конвекции жидкостей в больших сосудах используют критериальное уравнение, связывающее критерии Нусельта (Nu), Грасгофа (Gr) и Прандтля (Pr) :
Nu = C×(Gr×Pr)m, (4.27)
где 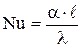 ; (4.28)
; (4.28)
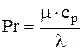 ; (4.29)
; (4.29)
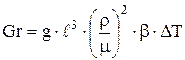 , (4.30)
, (4.30)
C и m - константы, зависящие от произведения критериев (Gr×Pr), формы и положения поверхности теплообмена (табл. 4.1) [22].
Таблица 4.1.
Значения констант C и m в уравнении (4.27) [22]
| Форма и положение поверхности теплообмена | Определяющий линейный размер, 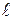
| Область применимости | С | m |
| Вертикальные пластины | Высота пластины | Gr×Pr<108 Gr×Pr>108 | 0.56 0.129 | 1/4 1/3 |
| Горизонтальные пластины: | ||||
| 1. Верхняя поверхность нагретой пластины | Ширина пластины | 105<Gr×Pr<2×107 2×107< Gr×Pr<3×1010 | 0.54 0.14 | 1/4 1/3 |
| 2. Нижняя поверхность нагретой пластины | Ширина пластины | 105<Gr×Pr<2×107 | 0,25 | 1/4 |
В критерии входят следующие величины:
l - коэффициент теплопроводности электролита, Вт/(м×град);
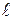 - линейный размер, определяющий процесс теплопередачи, м;
- линейный размер, определяющий процесс теплопередачи, м;
m - динамическая вязкость жидкости, Па×с;
ср - удельная теплоемкость электролита, Дж/(кг×град);
g - ускорение свободного падения, м/с2;
r - плотность электролита, кг/м3;
b - коэффициент объемного расширения жидкости, град-1,
DT - разность между температурой стенки и жидкости.
При расчете тепловых балансов электрохимических аппаратов тепло передается от растворов электролитов, представляющих собой сложные системы. Поэтому все характеристики рассчитывают исходя из закона Дальтона. Коэффициент объемного расширения
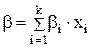 , (4.31)
, (4.31)
где bi - коэффициент объемного расширения i-го компонента, xi - массовая доля i-го компонента. Для большинства растворов массовая доля воды составляет 0,8 и больше, поэтому при расчетах в качестве b можно использовать коэффициент объемного расширения воды.
Вязкость смеси неполярных жидкостей можно определить [22] по формуле
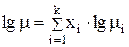 . (4.32)
. (4.32)
Однако для водных растворов зависимость вязкости от состава раствора неизвестна, поэтому при расчетах, как правило, используют вязкость воды.
Плотность растворов зависит от состава электролита (xi) и от температуры (T) по уравнению (3.72):
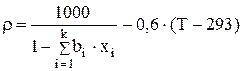 (4.33)
(4.33)
Для определения удельной теплопроводности растворов можно воспользоваться приближенным уравнением [22]

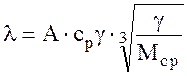 (4.34)
(4.34)
А - коэффициент, зависящий от степени ассоциации молекул жидкости: для неассоциированных жидкостей А=1.52, а для ассоциированных А=1.29;
g - относительная плотность (по отношению к воде);
Мср -средняя молекулярная масса зависит от массовой доли xi и молекулярной массы Mi i -го сорта частиц.
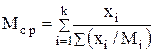 (4.35)
(4.35)
С помощью уравнений (4.27-4.30) производят расчет коэффициента теплоотдачи при свободной конвекции растворов (например, при конвективной передаче тепла от электролита к корпусу электролизера):
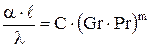 или
или 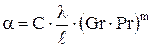 (4.36)
(4.36)
Величина критерия Грасгофа зависит от разницы температур теплоотдающей жидкости и тепловоспринимающей поверхности.
При теплообмене за счет свободной конвекции воздуха (например, передача тепла конвекцией с зеркала электролита или от корпуса электролизера к воздуху) можно пользоваться упрощенными уравнениями [22], приведенными в таблице 4.2.
Скорость передачи тепла по механизму теплопроводности через многослойную плоскую стенку [22] определяется по уравнению:
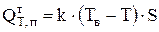 , Вт или Дж/с (4.37)
, Вт или Дж/с (4.37)
где k - коэффициент теплопередачи за счет теплопроводности, Дж/(м2×с×град), который зависит от количества различных слоев (M), толщины слоя (di) и его теплопроводности (li):
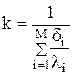 . (4.38)
. (4.38)
Таблица 4.2.
Уравнения теплоотдачи для воздуха при свободной конвекции.
| Форма и положение поверхности теплообмена | Определяющий размер | Коэффициент теплоотдачи, a, Вт/(м2×град) | |
 ,
град×м3 ,
град×м3
|  ,
град×м3 ,
град×м3
| ||
| Вертикальные пластины | Высота пластины | 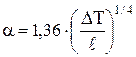
| 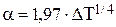
|
| Горизонтальные пластины, верхняя поверхность | Ширина пластины | 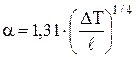
| 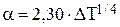
|
| Горизонтальные пластины, нижняя поверхность | Ширина пластины | 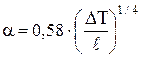
|
При передаче тепла через стенку или дно электролизера имеет место совместная теплопередача теплопроводностью, конвекцией и излучением. Тепло передается от горячего электролита к корпусу электролизера конвекцией, через многослойную стенку (сам корпус и его футеровка) теплопроводностью, а от корпуса к воздуху конвекцией и излучением:
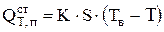 (4.39)
(4.39)
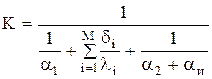 (4.40)
(4.40)
a1 - коэффициент теплоотдачи конвекцией от электролита к стенке ванны определяется величиной температуры корпуса со стороны электролита (Тст,э);
a2 и aи - соответственно, коэффициенты теплоотдачи конвекцией и излучением от наружной стороны стенки к воздуху, определяются температурой корпуса со стороны воздуха (Тст,в);
Т - температура электролита в электролизере;
Тв - температура окружающей среды.
При совместной теплопередаче поток тепла от электролита к стенке Q1 равен потоку тепло через стенку Q2 , а поток через стенку равен потоку тепла от наружной стороны стенки к воздуху Q3:
Q1=Q2 и Q2=Q3 (4.41)
С учетом механизма переноса имеем систему уравнений:
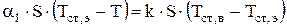 (4.42)
(4.42)
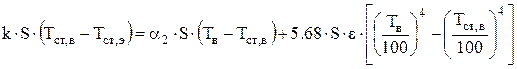 (4.43)
(4.43)
Коэффициент теплоотдачи конвекцией от электролита к внутренней стороне корпуса a1 зависит от разницы температур внутренней поверхности корпуса и электролита в соответствии с уравнением (4.36). Если учесть зависимость критерия Грасгофа от разницы температур, то получим
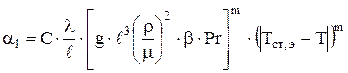 (4.44)
(4.44)
Коэффициент теплопередачи k не зависит от температуры и рассчитывается по уравнению (4.38).
Коэффициент теплоотдачи конвекцией от наружной стороны корпуса к воздуху a2 определяется по упрощенным формулам, представленным в таблице 4.2, и зависит от разницы температур окружающей среды Т2 и Тст,2. В общем виде это можно записать так:
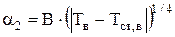 (4.45)
(4.45)
Здесь В константа (табл. 4.2), которая зависит от размера и положения поверхности теплообмена.
Система уравнений (4.42) - (4.45) содержит 4 неизвестных a1, a2, Тст,э и Тст,в. Она легко может быть решена в среде пакета MathCAD.
Коэффициент теплоотдачи излучением определяется из соотношения:
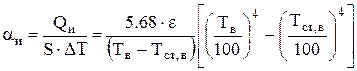 (4.46)
(4.46)
После этого известны все величины, необходимые для расчета коэффициента теплопередачи по уравнению (4.40) и потерь тепла корпусом или дном электролизера по уравнению (4.39).
Если на электродах выделяется газ или технологический процесс предполагает барботаж электролита газом, то необходимо учитывать унос тепла с газом, уходящим из электролизера. Унос тепла при массопереносе зависит от скорости выделения газа на электродах или скорости барботирующего газа в расчете на 1м2 зеркала электролита (qг, кг/(м2∙с)), удельной теплоемкости газа (ср,г, Дж/(кг∙град)) и разницы температур газа (Тг) и электролита (Т)
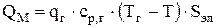 (4.47)
(4.47)
Sэл - площадь зеркала электролита. Скорость выделения газа на электродах определяется при расчете материального баланса (ур. 3.63 или 3.64).
4.2.4. Перенос тепла при переходе в другое агрегатное состояние
Процесс испарения воды сопровождается уносом тепла, что приводит к охлаждению электролита. Скорость передачи тепла зависит от интенсивности испарения воды и скрытой теплоты парообразования в соответствии со следующим уравнением:
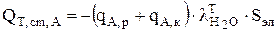 (4.48)
(4.48)
Необходимо учитывать равновесное испарение воды в объем выделяющегося или барботируемого газа 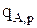 (ур.3.62) и конвективный унос паров воды
(ур.3.62) и конвективный унос паров воды 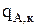 c поверхности зеркала электролита (ур.3.65).
c поверхности зеркала электролита (ур.3.65).
Скрытая теплота парообразования при температуре электролита 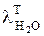 может быть рассчитана по формуле:
может быть рассчитана по формуле:
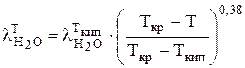 (4.49)
(4.49)
где 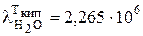 Дж/кг - удельная теплота парообразования при температуре кипения Ткип=373К; Ткр - критическая температура воды равная 647К;
Дж/кг - удельная теплота парообразования при температуре кипения Ткип=373К; Ткр - критическая температура воды равная 647К;
В заключение необходимо отметить, что на температуру электролита в электрохимическом аппарате могут оказывать влияние следующие источники тепла: изменение тепла за счет протекания химических реакций (4.19), разогрев электролита в результате прохождения электрического тока (4.20), потери тепла с зеркала электролита по механизму излучения (.4.25) и конвекции (4.26), передача тепла через стенки и дно аппарата (4.39), перенос тепла с газом (4.47) и при испарении воды (4.48). После суммирования всех источников тепла по уравнению 4.14 и расчета теплоемкости всех потоков (4.4) можно рассчитать тепловой баланс.
4.3. Расчет стационарного теплового баланса ванны рафинирования меди
Цель расчета стационарного теплового баланса ванны рафинирования меди состоит в том, чтобы определить, какова должна быть температура поступающего в электролизер раствора, чтобы в нем поддерживалась постоянная температура, равная 600С.
Математическая модель стационарного теплового баланса представлена уравнениями 4.12-4.13:
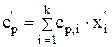 (4.12)
(4.12)
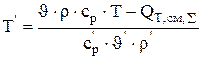 (4.13)
(4.13)
Для расчета теплового баланса необходимы значения скорости и плотности потока циркуляции на входе в электролизер ( 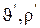 ) и на выходе из него (
) и на выходе из него ( 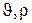 ). Указанные величины находятся в результате решения материального баланса электролизера. Концентрации компонентов во входящем потоке были найдены в ходе решения стационарного материального баланса (см. разд. 3.2.1.5). Скорость циркуляции электролита на выходе из ванны равна
). Указанные величины находятся в результате решения материального баланса электролизера. Концентрации компонентов во входящем потоке были найдены в ходе решения стационарного материального баланса (см. разд. 3.2.1.5). Скорость циркуляции электролита на выходе из ванны равна 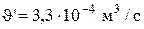 . Расчеты показывают, что для поддержания постоянного состава электролита в ванне (100г/л CuS04, 44,8г/л NiS04 и 190г/л H2S04), циркуляционный поток на входе в ванну должен иметь следующий состав: 97,91 г/л CuS04, 44,18 г/л NiSO4, и 188,76 г/л H2SO4. Подаваться электролит в ванну должен со скоростью
. Расчеты показывают, что для поддержания постоянного состава электролита в ванне (100г/л CuS04, 44,8г/л NiS04 и 190г/л H2S04), циркуляционный поток на входе в ванну должен иметь следующий состав: 97,91 г/л CuS04, 44,18 г/л NiSO4, и 188,76 г/л H2SO4. Подаваться электролит в ванну должен со скоростью 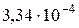 м3/с.
м3/с.
Далее следует определить теплоемкость электролита в электролизере ( 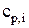 ) и во входящем потоке (
) и во входящем потоке ( 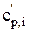 ):
):
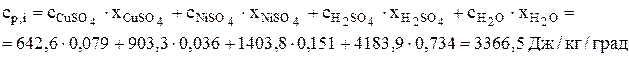
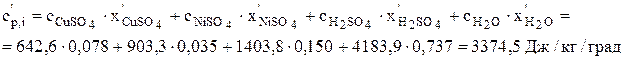 Теплоемкости отдельных компонентов берутся в справочниках физико-химических величин [23].
Теплоемкости отдельных компонентов берутся в справочниках физико-химических величин [23].
Основную сложность при составлении теплового баланса представляет собой расчет суммарной интенсивности источников тепла 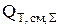 в электролизере.
в электролизере.
1. Источник тепла за счет протекания химической реакции растворения медных анодов под действием кислорода
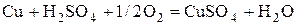
зависит от скорости этой реакции (разд. 3.2.1.3, 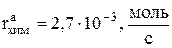 ) и изменения энтальпии (ур. 4.15):
) и изменения энтальпии (ур. 4.15):
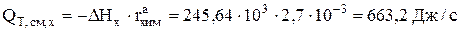
где 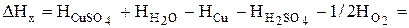
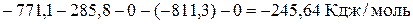
Отрицательное значение величины DH свидетельствует о том, что химическая реакция сопровождается выделением тепла.
2. Количество выделяющегося тепла в результате прохождения электрического тока рассчитывается по уравнениям (4.20÷4.22):
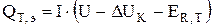 , где
, где 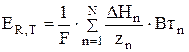
Напряжение на электролизере равно 0,34В, падение напряжения в шинах и контактах 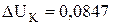 [3]. При расчете теплового э.д.с. разложения необходимо учитывать, что, в соответствии с принятыми допущениями (разд. 3.2.1.3) на аноде происходит растворение не только меди, но и никеля, тогда как на катоде восстанавливаются только ионы меди:
[3]. При расчете теплового э.д.с. разложения необходимо учитывать, что, в соответствии с принятыми допущениями (разд. 3.2.1.3) на аноде происходит растворение не только меди, но и никеля, тогда как на катоде восстанавливаются только ионы меди:
Анод 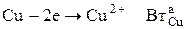 (1)
(1)
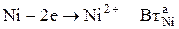 (2)
(2)
Катод 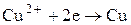 (3)
(3)
Тогда можно записать
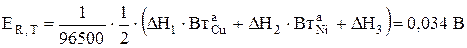
В результате прохождения через электролит тока величиной 15360 А выделяется следующее количество тепла:
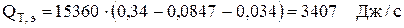
В соответствии с технологическим регламентом температура электролита равна 600С, поэтому в процессе работы электролизера происходят потери тепла с поверхности электролита, через стенки и дно ванны.
3. Потери тепла с поверхности электролита (Sэл=2,36м2) по механизму излучения (ур. 4.25) равны:
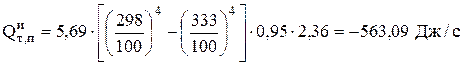
Степень черноты излучающей поверхности для раствора близок к значению e=0,95 для воды [22].
4. На границе электролит-воздух происходит передача тепла по механизму конвекции (ур. 4.26):
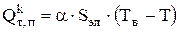
Для того чтобы найти коэффициент теплоотдачи, можно воспользоваться уравнениями табл.4.2. Для этого проверяют значение параметра:
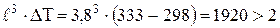 , где
, где 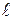 - ширина электролизера.
- ширина электролизера.
И для горизонтальной пластины по табл 4.2 выбираем:
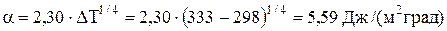
Тогда потери тепла с зеркала электролита за счет конвекции равны:
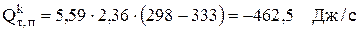
5. Потери тепла с зеркала электролита в результате испарения воды рассчитываются по ур.4.48:
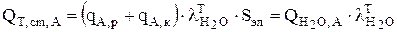
Интенсивность испарения воды была рассчитана в материальном баланса (разд. 3.2.1.3) 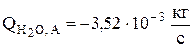 .
.
Скрытая теплота парообразования при температуре электролита 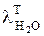 равна (ур. 4.49):
равна (ур. 4.49): 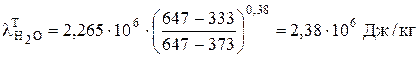 .
.
Тогда 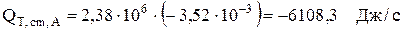 .
.
6. При расчете потерь тепла через стенки и дно электролизера необходимо учитывать передачу тепла по механизмам конвекции от электролита к стенке, теплопроводности через многослойную стенку, конвекции от стенки к воздуху и излучения (4.42-4.43).
Коэффициент теплоотдачи при передаче тепла от электролита к стенке рассчитывают из критерия Нуссельта (ур. 4.28) [22]:
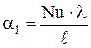 ,
,
где в соответствии с ур. 4.27 Nu = C×(Gr×Pr)m. Чтобы найти коэффициенты C и m в критериальном уравнении, необходимо рассчитать произведение критериев Прандтля и Грасгофа и воспользоваться таблицей 4.1. Значения параметров, входящих в критерии взяты из справочников [18,21-23].
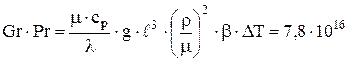 . Принимаем допущение, что разница температуры электролита и температуры стенки со стороны электролита для расчета критерия Грасгофа равна
. Принимаем допущение, что разница температуры электролита и температуры стенки со стороны электролита для расчета критерия Грасгофа равна 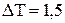 .
.
В соответствии с таблицей 4.1 для вертикальной пластины (боковой стенки электролизера) и Gr×Pr>108 C=0,129 и m=1/3. В результате совместного решения ур. 4.27÷4.30 получили, что коэффициент теплоотдачи зависит от температуры стенки со стороны электролита 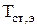 :
:
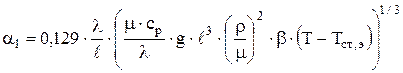 ,
,
Коэффициент теплопередачи за счет теплопроводности (k) через многослойную стенку зависит от толщины слоев и их теплопроводности (ур. 4.38). Электролизер для рафинирования меди выполняется из железобетона толщиной 14 см, внутри ванна футерована винипластом толщиной 10мм. Тогда имеем: 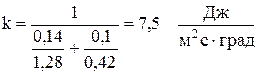 .
.
Для расчета коэффициента теплоотдачи при свободной конвекции в воздух (a2) необходимо воспользоваться табл.4.2. Для стенки 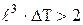 (здесь
(здесь 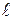 - высота стенки электролизера), поэтому для вертикальной пластины выбираем выражение, в соответствии с которым коэффициент a2 зависит от температуры стенки со стороны воздуха:
- высота стенки электролизера), поэтому для вертикальной пластины выбираем выражение, в соответствии с которым коэффициент a2 зависит от температуры стенки со стороны воздуха:
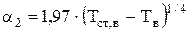
Теперь можно записать систему уравнений 4.42-4.43 для определения температуры стенки со стороны электролита и температуры стенки со стороны воздуха.
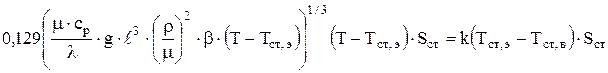

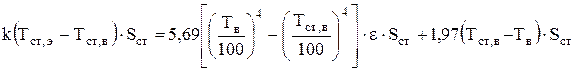
Здесь Sст - площадь стенок электролизера, e=0,8 - степень черноты излучающей поверхности для железобетона.
В результате решения данной системы уравнений в пакете Mathcad были определены 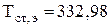 и
и 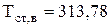 .
.
После этого определяем значения коэффициентов теплоотдачи
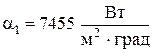 и
и 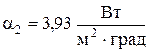
коэффициента теплоотдачи излучением
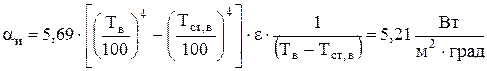
Окончательно коэффициент теплопередачи через стенку (ур.4.40) равен
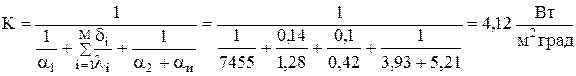 ,
,
а потери тепла через стенки электролизера (4.39)
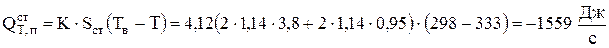 .
.
Потери тепла через дно электролизера 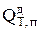 рассчитываются в таком же порядке, как и потери через стенки. Однако, при выборе формул для расчета коэффициентов теплоотдачи по таблицам 4.1 и 4.2 необходимо выбирать строки «горизонтальная пластина, нижняя поверхность». Потери тепла через дно составили
рассчитываются в таком же порядке, как и потери через стенки. Однако, при выборе формул для расчета коэффициентов теплоотдачи по таблицам 4.1 и 4.2 необходимо выбирать строки «горизонтальная пластина, нижняя поверхность». Потери тепла через дно составили 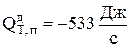 .
.
Завершает расчет стационарного теплового баланса определение температуры потока циркуляции на входе в электролизер (ур.4.13):
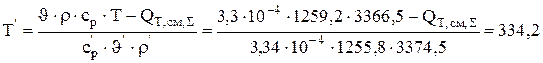
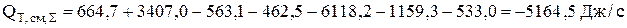 Проведенный расчет показал, что для того, чтобы поддерживать в электролизере постоянную температуру электролита 600С необходимо подавать на вход электролит с температурой 61,20С.
Проведенный расчет показал, что для того, чтобы поддерживать в электролизере постоянную температуру электролита 600С необходимо подавать на вход электролит с температурой 61,20С.
Дата добавления: 2016-06-05; просмотров: 2249;











