Кооперативная теория
Другим классом неантагонистических игр являются кооперативные игры.
Каждая бескоалиционная игра описывает некоторый, вообще говоря, достаточно сложный конфликт, не всегда поддающийся не только детальному изучению, но и даже точному описанию. Поэтому иногда представляется естественным выбирать в этом конфликте отдельные его аспекты и подвергать их специальному анализу.
Самым простым будет при этом выделение некоторого множества игроков 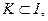 называемого коалицией (бескоалиционность рассматриваемых игр в том и состоит, что никакие коалиции первоначально в правилах игры не предусмотрены), и рассмотрение антагонистической игры
называемого коалицией (бескоалиционность рассматриваемых игр в том и состоит, что никакие коалиции первоначально в правилах игры не предусмотрены), и рассмотрение антагонистической игры 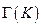 )коалиции
)коалиции 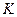 как единого игрока против ее «окружения»
как единого игрока против ее «окружения» 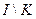 в целом. При этом комбинации стратегий игроков из
в целом. При этом комбинации стратегий игроков из 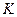 (и из
(и из 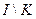 ) составляют стратегии
) составляют стратегии 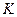 (соответственно стратегии
(соответственно стратегии 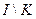 ), а сумма выигрышей игроков из
), а сумма выигрышей игроков из 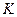 - выигрыш коалиции
- выигрыш коалиции 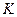 . Значение
. Значение 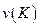 этой игры естественно понимать как силу коалиции
этой игры естественно понимать как силу коалиции 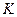 в общей игре
в общей игре 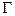 .
.
Соответствие 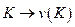 для каждой коалиции
для каждой коалиции 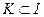 в условиях бескоалиционной игры
в условиях бескоалиционной игры 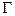 называется ее характеристической функцией и обозначается через
называется ее характеристической функцией и обозначается через 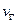 .
.
Характеристическая функция 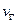 дает представление о возможностях коалиций и отдельных игроков в условиях игры
дает представление о возможностях коалиций и отдельных игроков в условиях игры 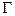 даже без указания множества стратегий и функций выигрыша в ней. Поэтому говорят даже о задании игр «в форме характеристической функции», противопоставляя его заданию игр «в нормальной форме», и в других формах, которые существуют, но нами не затрагиваются. Изучение характеристических функций игр и составляет содержание кооперативной теории игр.
даже без указания множества стратегий и функций выигрыша в ней. Поэтому говорят даже о задании игр «в форме характеристической функции», противопоставляя его заданию игр «в нормальной форме», и в других формах, которые существуют, но нами не затрагиваются. Изучение характеристических функций игр и составляет содержание кооперативной теории игр.
В рамках такой кооперативной теории исходами игры будут некоторые распределения суммарного выигрыша, называемые дележами. Характеристическую функцию, рассматриваемую совместно с некоторым множеством дележей, принято называть кооперативной игрой. Для кооперативных игр конструируются соответствующие принципы оптимальности, и рассматривается связанная с ними проблематика.
В некоторых из этих принципов оптимальности воплощаются представления об устойчивости, которые получаются перенесением на соотношения между дележами различных вариантов описания максимума функции. Однако применительно к дележам эти варианты определения перестают быть эквивалентными и порождают различные принципы оптимальности.
Вводимые принципы оптимальности имеют некоторые недостатки (если вообще можно говорить о недостатках достаточно естественно возникающих объектов): они не всегда реализуемы, а в тех случаях, когда реализуемы, могут допускать целые множества реализации, причем каждая реализация может состоять из многих дележей. К тому же реализации этих принципов могут не удовлетворять условиям справедливости в том смысле, как она определялась выше.
Все отмеченное заставляет искать новые принципы оптимальности. При этом плодотворным оказывается следующий путь: не переносить на случай дележей те или иные формулировки для максимумов на числовых множествах, выясняя, какими свойствами полученные принципы оптимальности будут обладать, а наоборот, фиксировать те свойства (в том числе - некоторые черты справедливости), которые желательно видеть у интересующих нас принципов оптимальности, и конструировать принцип, который этими свойствами заведомо будет обладать.
Дата добавления: 2017-04-05; просмотров: 1430;











