Расчет повышения давления и скорости ударной волны

Величину повышения давления ∆p_уд при гидравлическом ударе в трубопроводе можно определить, рассматривая элементарное перемещение ударной волны dx за время dt (рис. 8.4).

Применим к элементу трубы dx теорему об изменении количества движения:

.

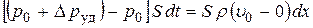Тогда скорость распространения ударной волны

,

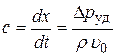откуда получаем

.

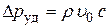(8.1)

Выражение (8.1), определяющее величину повышения давления при гидравлическом ударе, называют формулой Жуковского.

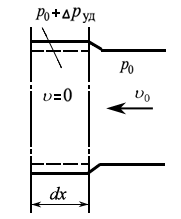
Рис. 8.4

Скорость ударной волны c нам пока неизвестна, поэтому попробуем определить ударное давление ∆p_уд из того условия, что кинетическая энергия жидкости переходит в работу деформации: растяжения стенок трубы и сжатия жидкости.

Кинетическая энергия жидкости в трубе радиуса r, длиной l, движущейся со скоростью 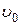будет

.

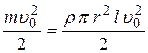(8.2)

Работа деформации равна потенциальной энергии деформированного тела и составляет половину произведения силы на удлинение. Из рис. 8.5.а видно, что работа по растяжению стенок трубы совершается силами давления на пути ∆r. Такая работа будет равна

.

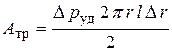Нормальное напряжение в материале стенки трубы 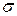связано с давлением ∆p_уд и толщиной стенки 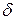соотношением:

.

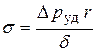(8.3)

По закону Гука:

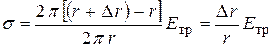
(8.4)

где 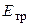– модуль упругости материала стенок трубы.

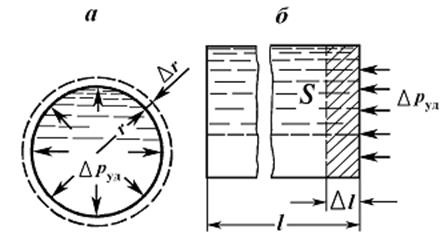
Рис. 8.5

Выразим из уравнения закона Гука (8.4) величину :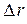

,

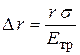а величину 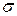возьмем из уравнения (8.3). Тогда работа деформации стенок трубы будет равна

.

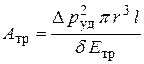(8.5)

Работу сжатия жидкости объемом V представим как работу сил давления на пути 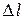(рис. 8.5.б):

.

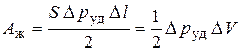Связь между относительным изменением объема жидкости и вызвавшим это изменение давлением определяется, как известно, модулем упругости K (обратным коэффициенту объемной сжимаемости):

.

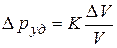Приняв за V объем жидкости в трубе, получим выражение для работы сжатия жидкости:

.

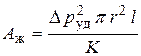(8.6)

Окончательно уравнение энергий запишем, объединяя формулы (8.2), (8.5) и (8.6):

= + .

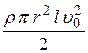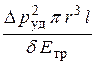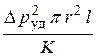Решая его относительно 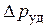, находим

.

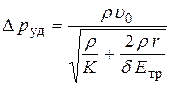(8.7)

Сравнивая это выражение с формулой Жуковского (8.1), получаем выражение для скорости ударной волны:

.

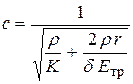(8.8)

Формулы (8.1) и (8.8) получены с использованием некоторых упрощающих допущений:

· в жидкости отсутствуют трение и другие виды потерь энергии при ударе;

· движение жидкости в трубопроводе принято одномерным, то есть все местные скорости считаем равными средней скорости, а давление – одинаковым во всех точках живого сечения;

· при деформациях трубы и сжатии жидкости справедлив закон Гука.

И, тем не менее, экспериментальные исследования гидравлического удара в трубе показывают, что если жидкость не содержит воздушных примесей и начальное давление p₀ не велико, то, несмотря на перечисленные упрощающие допущения, формула Жуковского достаточно хорошо соответствует опытным данным. При высоких начальных значениях давления p₀ и больших 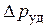скачок давления 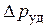получается несколько большим, чем по формуле Жуковского. Это объясняется тем, что изменяется (увеличивается) модуль K, то есть нарушается линейность изменения деформации по давлению.

Если предположить, что труба имеет абсолютно жесткие (а не упругие) стенки, то есть 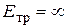, то из формулы (8.8) получаем, что скорость ударной волны составит

,

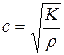то есть будет равна скорости звука в однородной упругой среде с плотностью 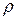и объемным модулем K. Для воды эта скорость равна 1 435 м/с. Но так как стенки трубы не абсолютно жесткие, то скорость ударной волны меньше скорости звука.

Если скорость жидкости в трубе уменьшается не до нуля, а до некоторого значения 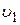(это происходит при неполном закрытии крана), то возникает неполный гидравлический удар, и формула Жуковского будет иметь вид

.

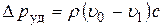(8.9)

Формула Жуковского справедлива при очень быстром перекрытии сечения трубопровода, при котором время закрытия

.

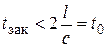(8.10)

Величина t₀ называется фазой гидравлического удара.

При выполнении условия (8.10) имеет место прямой гидравлический удар.

Если t_зак > t₀ возникает непрямой гидравлический удар, при котором ударная волна, отразившись от резервуара, возвращается к крану, перекрывающему трубопровод, раньше, чем он будет закрыт. Понятно, что повышение давления 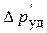при этом будет меньше, чем 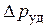при прямом ударе.

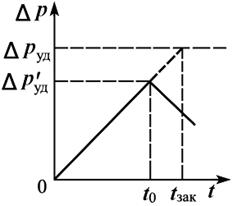
Рис. 8.6

Если предположить, что скорость потока при закрытии крана уменьшается линейно, и давление возрастает линейно во времени (рис. 8.6), то

,

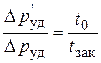откуда

.

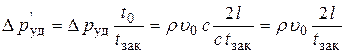(8.11)

Рассмотрим еще случай, когда тупиковый трубопровод с начальным давлением p₀ отделен краном от сосуда большого объема (или насоса) с высоким давлением p₁ (рис. 8.7).

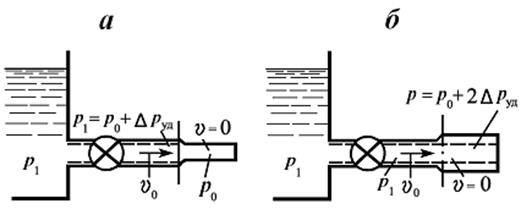
Рис. 8.7

При мгновенном открытии крана давление в начале трубопровода внезапно возрастает на 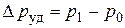. Возникшая волна давления со скоростью c перемещается к концу трубопровода, давление за ее фронтом отличается от давления перед фронтом на .

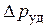Скорость жидкости в плоскости фронта возрастает от нуля до значения 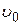, определяемого из формулы Жуковского (8.1):

.

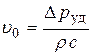В момент подхода фронта ударной волны к тупиковому концу трубы давление во всем трубопроводе увеличивается на 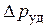и жидкость приобретает скорость 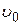. У тупикового конца трубы скорость жидкости полностью гасится, дополнительно увеличивая давление еще на 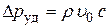. И от тупикового конца к крану по трубопроводу начинает двигаться новая (отраженная) волна давления, за фронтом которой давление по сравнению с первоначальным возросло на 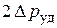, а скорость жидкости .

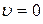Способы предотвращения или смягчения гидравлического удара могут быть различными. Наиболее эффективным способом снижения 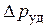является устранение возможности прямого гидравлического удара. Для этого при заданной длине трубопровода необходимо увеличивать время срабатывания кранов, задвижек и других устройств. Другой способ – установка перед кранами и задвижками компенсаторов в виде дополнительных объемов жидкости, гидроаккумуляторов или предохранительных клапанов.

Уменьшение скорости движения жидкости в трубопроводе (путем увеличения диаметра труб при заданном расходе) и уменьшение длины трубопровода (для получения непрямого удара) тоже смягчает удар, снижая ударное давление.

И, наконец, иногда просто увеличивают прочность слабых элементов системы трубопроводов.