Расчет группы болтов

Расчет таких соединений сводится к определению нагрузки для наиболее нагруженного болта. Затем рассчитывают прочность этого болта по формулам одного из случаев, рассмотренных выше.

В расчетах приняты следующие допущения:

1. Поверхности стыка остаются плоскими (недеформируемыми) при всех фазах нагружения;

2. Поверхности стыка имеют минимум две оси симметрии, а болты расположены симметрично относительно этих осей;

3. Все болты соединения одинаковы и ровно затянуты.

С некоторым приближением перечисленные условия справедливы для большинства конструкций.

Различают три характерных случая расчета соединений, включающих группу болтов.

I. Расчет группы болтов, нагруженных сдвигающей силой, проходящей через центр жесткости соединения и лежащей в плоскости стыка:

а) болт в отверстие поставлен без зазора (рис. 20.2). Расчет производится по напряжениям среза и смятия

,

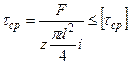где z – число болтов, i – число плоскостей среза.

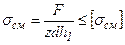- для верхней детали;

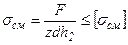- для нижней детали.

б) болт поставлен в отверстие с зазором (рис. 20.3). Условие равновесия

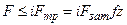или

.

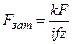Расчетная нагрузка .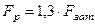

Условие прочности

,

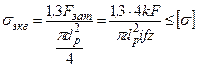откуда .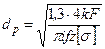

II Расчет группы болтов, нагруженных моментом, приложенным в плоскости стыка (рис. 20.4).

Внешний момент Т должен уравновешиваться моментами внутренних сил трения, которые вызываются затяжками болтов и лежат в плоскости стыка.

Расчетная нагрузка

.

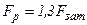Условие равновесия

.

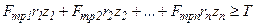Усилия затяжки равны, следовательно

,

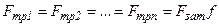тогда 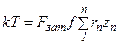или .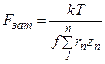

Здесь z_n – число болтов, равноудаленных от центра симметрии стыка.

Частный случай - фланцевое крепление.

В этом случае 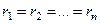(рис. 20.5) и тогда .

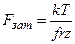Затем болты рассчитываются по эквивалентному напряжению. Если группа болтов поставлена без зазора, то внешняя нагрузка воспринимается непосредственно болтами и они рассчитываются по напряжениям среза и смятия.

II. Расчет группы болтов нагруженных моментом приложенным перпендикулярно плоскости стыка.

Нагрузка соединения раскрывает стык деталей. При раскрытии стыка ось поворота смещается от оси симметрии к кромке стыка. Определим наибольшую нагрузку на болт по этой нагрузке. Условие равновесия соединения (рис. 20.6)

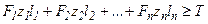, (20.1)

где z_n – число болтов равноудаленных от оси поворота; 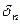- деформация n-го болта; l_n – плечо силы n-го болта.

Из подобия треугольников (рис. 20.6)

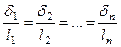, но по закону Гука 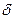~ F, тогда

.

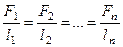Выразим все усилия через максимальное усилие F₁.

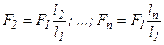, тогда уравнение (20.1) перепишется в виде

,

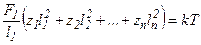где k – коэффициент запаса.

Отсюда 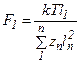. Расчетная нагрузка F_p=1,3F₁.

Лекция №21