Определение момента, необходимого для затяжки резьбовой пары
 При затягивании резьбовой пары детали прижимаются друг к другу с силой Fзат (рис 16.8). Со стороны деталей на головку болта и гайку действует также сила Fзат, которая через резьбу передается на стержень болта и вызывает его растяжение. Затяжка производится ключом с усилием Fкл, который создает момент Tкл=FклL. Момент внешней силы Fкл уравновешивается моментом внутренних сил трения в резьбе и на торце гайки. Таким образом
При затягивании резьбовой пары детали прижимаются друг к другу с силой Fзат (рис 16.8). Со стороны деталей на головку болта и гайку действует также сила Fзат, которая через резьбу передается на стержень болта и вызывает его растяжение. Затяжка производится ключом с усилием Fкл, который создает момент Tкл=FклL. Момент внешней силы Fкл уравновешивается моментом внутренних сил трения в резьбе и на торце гайки. Таким образом
Ткл=Тр+Тт,
где Тр – момент трения в резьбе; Тт- момент трения на торце гайки.
Болт находится в сложнонапряженном состоянии – скручивается и растягивается от осевой силы. Определим каждую из составляющих Tкл.
 1. Определение момента трения на торце гайки.При затяжке резьбовой пары, когда торец гайки касается поверхности детали, возникает момент сил трения на поверхности гайки (рис 16.9). Введем допущение: усилие затяжки равномерно распределено по торцевой поверхности гайки. Под действием усилия Fзат на торце гайки возникает давление
1. Определение момента трения на торце гайки.При затяжке резьбовой пары, когда торец гайки касается поверхности детали, возникает момент сил трения на поверхности гайки (рис 16.9). Введем допущение: усилие затяжки равномерно распределено по торцевой поверхности гайки. Под действием усилия Fзат на торце гайки возникает давление
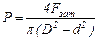 ,
,
где d– диаметр отверстия, D– диаметр под ключ. Проведем две концентрические окружности с радиусами r и r+dr. Выделяем элемент торца гайки dj . На этот элемент действует нормальная сила
dFn=PdS=Prdjdr,
где dS-площадь выделенного элемента. Рис.16.9
Элементарная сила трения определяется как
dFтр=dFnf=PdS=Pfrdjdr,
где f – коэффициент трения на торце гайки. Элементарный момент трения
dTT =dFтрr= Pfr2djdr.
Тогда момент трения на торце гайки определяется в виде
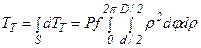 или
или 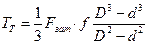 .
.
 |

 2. Определение момента трения в резьбе. Рассмотрим взаимодействие гайки и витка резьбы болта, которое можно заменить действием груза на наклонную плоскость (рис 16.10,а). Развернем виток резьбы на плоскость.
2. Определение момента трения в резьбе. Рассмотрим взаимодействие гайки и витка резьбы болта, которое можно заменить действием груза на наклонную плоскость (рис 16.10,а). Развернем виток резьбы на плоскость.
Под действием сил Fзат, Ft и R тело находится в равновесии. Из треугольника сил (рис. 16.10,б) имеем
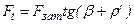 ,
,
где b - угол подъема витка резьбы, r’ – угол трения.
Определим момент трения в резьбе
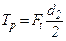 или
или 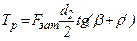 .
.
Условия самоторможения резьбы


 Самотормозящаяся резьба - это такая, в которой гайка удерживается под нагрузкой за счет сил трения. При свинчивании гайки сила трения Fтр меняет свое направление и условный груз находится в равновесии под действием сил Fзат, Ft и R (рис 16.11, а).
Самотормозящаяся резьба - это такая, в которой гайка удерживается под нагрузкой за счет сил трения. При свинчивании гайки сила трения Fтр меняет свое направление и условный груз находится в равновесии под действием сил Fзат, Ft и R (рис 16.11, а).
Из треугольника сил (рис 16.11,б)
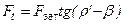
Условие самоторможения Ft>0, то есть в самотормозящейся резьбе для свинчивания гайки нужно обязательно приложить усилие Ft. В несамотормозящейся резьбе это усилие не нужно, так как гайка будет сама откручиваться под действием усилия затяжки Fзат (вес груза), тогда 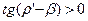 или
или 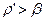 .
.
 Для метрической крепежной резьбы
Для метрической крепежной резьбы 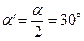 (рис 16.12), тогда
(рис 16.12), тогда
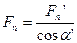 ;
; 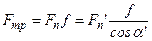 ,
,
где 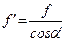 -приведенный коэффициент трения.
-приведенный коэффициент трения.
Угол трения 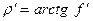 изменяется в зависимости от величины коэффициента трения в пределах от 6° (f=0,1) до 16° (f=0,3), а b лежит в пределах от 1,5° до 4°, т. е. все крепежные резьбы самотормозящиеся.
изменяется в зависимости от величины коэффициента трения в пределах от 6° (f=0,1) до 16° (f=0,3), а b лежит в пределах от 1,5° до 4°, т. е. все крепежные резьбы самотормозящиеся.
В прямоугольной ходовой резьбе сила Fn' перпендикулярна профилю витка, т.е. Fn'=Fn (рис 16.13). Отсюда находим Fтр= Fn f= Fn'f. В ходовых резьбах коэффициент трения ниже, чем в метрических f < f' , так как cosa <1.
Лекция №17
КПД резьбовой пары
Представим развертку витка резьбы с грузом на плоскости (рис 17.1). Рассмотрим случай навинчивания гайки, что соответствует подъему груза по наклонной плоскости.
 К.П.Д. резьбовой пары
К.П.Д. резьбовой пары
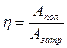 ,
,
где Апол – полезная работа,
Азатр – затраченная работа.
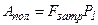 ,но
,но 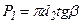 ,тогда
,тогда 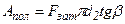 .
.
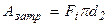 , но
, но 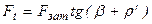 следовательно
следовательно 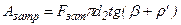 .
.
Тогда 
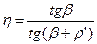 (17.1)
(17.1)
В самотормозящей паре b<r' и h< 0,5. КПД винтовой пары представляет интерес главным образом для винтовых механизмов. Последняя формула позволяет отметить, что h возрастает с увеличением b и уменьшением r'
График зависимости h от b при r'= 60 (рис. 17.2) имеет максимум. Максимальное значение h можно определить из выражения (17.1), приравняв нулю производную 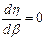 . Получим hmax при
. Получим hmax при 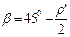 .
.
Для увеличения угла подъема резьбы применяются в винтовых механизмах многозаходные резьбы. Обычно b не превышает 250, так как дальнейший прирост КПД незначителен, а изготовление резьбы затруднено. Для повышения КПД винтовых механизмов применяют средства, снижающие трение в резьбе: антифрикционные материалы, смазку поверхностей, применение шариковых винтовых пар.
Распределение нагрузки по виткам резьбы
Рассмотрим схему винтовой пары (рис. 17.3).Основная осевая нагрузка Fзат винта передается через резьбу гайке и уравновешивается реакцией её опоры. При этом каждый виток резьбы нагружается соответственно силами
F1, F2,…, Fn, причем 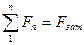 .
.

 |
При равномерном распределении нагрузки в резьбе F1=F2=…= Fn= Fзат/n, где n- число витков резьбы, эпюра распределения нагрузки по виткам имела бы вид как на рис.17.3, а. В реальных условиях распределение осевой силы между витками резьбы было бы равномерным, если бы резьба была изготовлена абсолютно точно, не изнашивалась и податливость резьбы была бы значительно выше податливости винта и гайки. В действительности эти условия отсутствуют. Влияние податливости винта на распределение сил между витками удобно показать для случая ввинчивания винта в массивную деталь, приняв её недеформируемой. Изобразим условно каждую пару витков в виде балочек, защемленных между стержнем винта и телом гайки.
На рис. 17.4,а показано резьбовое соединение в ненагруженном состоянии - балочки, изображающие витки резьбы, не деформированы.

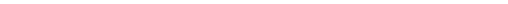
На рис. 17.4, б показано соединение, где податливость резьбы значительно больше податливости деталей, поэтому все витки имеют одинаковую деформацию и нагрузку.
На рис. 17.4, с показано соединение, у которого податливость стержня винта соизмерима с податливостью резьбы, поэтому нижние витки резьбы получили большее упругое перемещение, чем верхние, а сила между каждой парой витков винта и гайки по закону Гука пропорциональна упругим перемещениям этих витков. Неравномерность распределения нагрузки по виткам усугубляется тем, что витки на наиболее растянутой части винта сопряжены с витками, расположенными в наиболее сжатой части гайки. Например, в рассматриваемом случае винт растягивается, а гайка сжимается. При этом точки А, B, C и D винта и гайки перемещаются вниз соответственно на ΔA,ΔB,ΔC иΔD. Из – за растяжения участка AB винта имеем
ΔB < ΔA, (17.2)
а вследствие сжатия участка CD гайки
ΔD < ΔC. (17.3)
Выразим прогиб витка резьбы через относительное перемещение точек A и D (Δ AD), а также B и C (Δ BC):

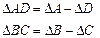 (17.4)
(17.4)
Из системы (17.4) получаем 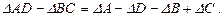
Согласно неравенствам (17. 2) и (17. 3) 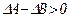 и
и 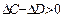 , следовательно
, следовательно
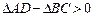 и
и 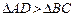 .
.
Все деформации витка резьбы и в том числе и прогиб пропорциональны его нагрузке, следовательно, нагрузка первого витка больше нагрузки второго и т.д.
Теоретическое решение о распределении нагрузки по виткам резьбы дано Н.Е. Жуковским в 1902 году. В дальнейшем это решение неоднократно подтверждалось экспериментальными исследованиями. Установлено, например, что при стандартной крепежной гайке с шестью витками, первый виток резьбы воспринимает 52% нагрузки, второй 25%, третий 12% и последний шестой – только 2% нагрузки.
При столь неравномерном распределении нагрузки по виткам резьбы большое увеличение высоты гайки оказывается бесполезным в связи с опасностью последовательного «цепного» разрушения витков. Приближенно – равномерное распределение нагрузки по виткам резьбы можно получать, только применяя гайки специальной формы, выравнивающие распределение нагрузки в резьбе. Специальные гайки желательно применять при действии переменных и динамических нагрузок, где разрушение носит усталостный характер.
 Висячая гайка.Выравнивание нагрузки в резьбе здесь достигается благодаря тому, что винт и гайка имеют однозначные деформации растяжения (рис. 17.5). При этом равенство (17.3) изменится и будет ΔD >ΔC, а разность между ΔAD и ΔBC уменьшится. Кроме того, в наиболее нагруженной зоне (внизу) висячая гайка обладает повышенной податливостью, что также способствует выравниванию нагрузки в резьбе.
Висячая гайка.Выравнивание нагрузки в резьбе здесь достигается благодаря тому, что винт и гайка имеют однозначные деформации растяжения (рис. 17.5). При этом равенство (17.3) изменится и будет ΔD >ΔC, а разность между ΔAD и ΔBC уменьшится. Кроме того, в наиболее нагруженной зоне (внизу) висячая гайка обладает повышенной податливостью, что также способствует выравниванию нагрузки в резьбе.
Гайка со срезанными витками.
У такой конструкции резьбовой пары увеличена податливость нижних витков винта, так как они соприкасаются с гайкой не всей поверхностью, а только своими вершинами (рис. 17.6). Увеличение податливых витков в наиболее нагруженной зоне снижает нагрузку этих витков.
Дата добавления: 2017-03-12; просмотров: 2321;











