Условия равновесия двухфазной однокомпонентной системы

Фазой называется макроскопическая, физически однородная часть системы, отличающаяся по физическим свойствам от других частей и отделенная от них четко выраженной границей.

Примерами двухфазных систем могут служить жидкость и ее насыщенный пар, кристалл и его расплав и т.д. Такие системы мы уже встречали ранее (см. § 12).

Рассмотрим однокомпонентную (т.е. состоящую из химически однородного вещества) систему, разделенную на две фазы a и b. Обозначим n_a - число молей вещества в фазе a, а n_b - в фазе b. Полное количество вещества n в системе остается постоянным (n = n_a + n_b = const).

Будем считать, что в системе установилось тепловое и механическое равновесие, т.е. температуры и давления в каждой из фаз одинаковы. Так как химический потенциал является функцией температуры и давления (m = m(Т,Р)), то химические потенциалы фаз тоже остаются неизменными.

Единственным процессом, возможным в системе при постоянстве Т и Р, является фазовый переход, т.е. переход вещества из одной фазы в другую. Для определения направления переноса вещества можно воспользоваться тем, что, как показано в предыдущем параграфе, термодинамический потенциал такой системы может только убывать ( 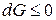). Представим термодинамический потенциал в виде

.

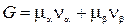Тогда .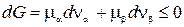

Так как n_a + n_b = const, то dn_a = -dn_b, и предыдущее соотношение можно переписать так

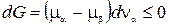. (22.1)

Отсюда следует, что при m_a > m_b dn_a < 0, т.е. G уменьшается при переходе вещества из фазы a в фазу b. При m_b > m_a dn_a > 0. Поток вещества направлен от фазы с большим химическим потенциалом к фазе с меньшим химическим потенциалом. По отношению к переходу вещества из одной фазы в другую химический потенциал играет такую же роль, какую температура играет для потока тепла или давление для потока газа в соответствующих процессах выравнивания. Уменьшение термодинамического потенциала прекратится, когда в системе останется только одна фаза.

Таким образом, если 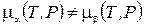, двухфазная система спустя некоторое время превратится в однофазную. Равновесие двух фаз возможно только при

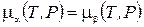. (22.2)

Это уравнение связывает значения температуры и давления, при которых две фазы могут сосуществовать. В принципе уравнение (22.2) позволяет выразить один из аргументов химического потенциала через другой, например Р = Р(Т), но для этого надо иметь аналитические выражения для химических потенциалов, которые далеко не всегда доступны. Однако можно и не зная конкретного вида формул m(Т,Р), найти зависимость Р от Т в дифференциальном виде. Для этого запишем дифференциалы химических потенциалов фаз

.

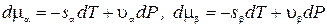Из (22.2) следует, что 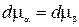, а значит 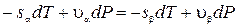или

,

.

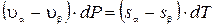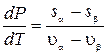В этом выражении разность молярных энтропий s_a -s_bможно связать с теплотой l_b-a, которую необходимо сообщить системе для перехода одного моля вещества из фазы b в фазу a.

.

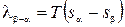Тогда

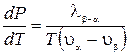. (22.3)

Это соотношение называется уравнением Клапейрона-Клаузиуса. Оно уже было получено ранее методом циклов (см. § 12).