Внешние силы и напряжения в корпусе судна
Определения и общие положения. Прочностью корпуса судна называется его способность противостоять внешним усилиям, возникающим в процессе эксплуатации судна, без нарушения целостности как всего корпуса, так и отдельных его конструктивных элементов. Прочности корпуса должна соответствовать необходимая жесткость, то есть способность сопротивляться внешним усилиям без значительных изменений формы конструкций. В большинстве случаев при удовлетворении требований к прочности жесткость оказывается достаточной.
Изучая прочность плавающего судна, его корпус рассматривают как пустотелую тонкостенную составную балку переменного по длине сечения, находящуюся под воздействием сложной системы сил, в число которых входят силы веса и инерции, гидростатические силы давления воды, гидродинамические силы, возникающие при движении судна, и тому подобное. Все эти силы в совокупности вызывают деформацию корпуса, которую в практических расчетах принято разделять на деформацию общего изгиба в продольной и поперечной плоскостях и местные деформации составных элементов корпуса. Соответственно рассматривают общую продольную прочность, поперечную прочность и местную прочность корпуса судна.
При характерных для морских судов соотношениях между высотой борта и шириной корпуса обеспечение общей продольной прочности в обычных условиях плавания на взволнованной поверхности моря приводит также и к обеспечению общей поперечной прочности, которую проверяют только в особых случаях (например, при постановке в док).
Кроме усилий, возникающих при общем изгибе корпуса, отдельные его конструкции воспринимают различные местные нагрузки. Например, набор и настил палубы воспринимают вес расположенных на палубе грузов, днище и борта – давление забортнойводы и т.д. Проверка прочности этих конструкций под действием таких местных нагрузок является задачей расчета местной прочности.
Внешние силы, вызывающие общий изгиб корпуса. При проверке общей продольной прочности корпуса судна рассматривают в условиях воздействия на него только вертикальной нагрузки – сил веса и вертикальных составляющих гидростатических и гидродинамических сил давления воды. Горизонтальные составляющие внешней нагрузки (упор движителей и силы сопротивления воды) не учитывают, так как общие напряжения в связях корпуса от таких сил пренебрежимо малы. Явление общего изгиба корпуса судна, плавающего на взволнованной поверхности воды, схематизируется. Изгибающие моменты, возникающие в различных поперечных сечениях корпуса, разделяют на три составляющие: на изгибающие моменты, возникающие при плавании судна на тихой воде; на дополнительные изгибающие моменты, возникающие при плавании на волнении в результате перераспределения сил плавучести по длине судна и на дополнительные динамические изгибающие моменты, действию которых судно периодически подвергается при ходе на полнении вследствие ударов днищем о воду. Соответственно разделяют и перерезывающие силы в поперечных сечениях корпуса.
Силы веса и вертикальные составляющие гидростатических сил давления воды (силы плавучести), действующие на судно, плавающее в положении статического равновесия на тихой воде, уравновешены в целом, т.е. их равнодействующие равны по абсолютному значению, противоположно направлены и приложены в точках, лежащих на одной вертикали. Однако по длине судна силы веса и плавучести распределены по различным законам, что приводит к возникновению перерезывающих сил и изгибающих моментов, а следовательно, и к общему продольному изгибу корпуса.
Распределение сил веса по длине судна определяется ступенчатой кривой сил веса (рис.7.1.а), а распределение сил плавучести – ступенчатой кривой сил плавучести (рис.7.1.б)
равновеликой по площади строевой по шпангоутам судна. Вычитая ординаты ступенчатой кривой сил плавучести из ординат ступенчатой кривой сил веса, получают ступенчатую кривую нагрузки q (рис.7.1.в). Согласно общей теории изгиба балок первая интегральная кривая от кривой нагрузки будет представлять собой кривую перерезывающих сил Q (рис.7.1.г), а вторая интегральная кривая - кривую изгибающих моментов M (рис.7.1.д). Все операции по построению указанных выше кривых в совокупности носят название постановки судна на тихую воду.
Ординаты кривой сил веса представляют в некотором выбранном масштабе силы веса, действующие на единицу длины судна. Для построения этой кривой длину судна разбивают на двадцать равных по длине участков – теоретических шпаций. Для упрощения расчетов принимают допущение, что в пределах каждой шпации вес распределяется равномерно, вследствие чего кривая получает ступенчатый вид. Исходным документом для построения кривой сил веса служит подробная таблица нагрузки судна, а также чертеж продольного разреза судна, при помощи которого отдельные статьи нагрузки распределяют по теоретическим шпациям. Предложено несколько способов (приемов) построения отдельных составных частей кривой сил веса, в частности кривой сил веса корпуса. Подробное рассмотрение этих способов, представляющее интерес лишь для инженеров–кораблестроителей, выполняющих расчеты общей прочности, выходит за пределы данного курса. Укажем только, что необходимыми условиями правильности построения кривой служат равенство ее площади (с учетом принятых масштабов) водоизмещению судна и совпадение абсцисс ЦТ площади кривой и ЦТ судна.
Кривая сил плавучести представляет собой строевую по шпангоутам, ординаты которой умножены на удельный вес забортной воды и отложены в масштабе, принятом ранее при построении кривой веса. Для упрощения расчетов полученную таким образом главную кривую сил плавучести заменяют равновеликой ей по площади ступенчатой кривой (см. рис.7.1.б). Отметим, что площади и абсциссы ЦТ ступенчатых кривых сил веса и сил плавучести должны соответственно совпадать в связи с равновесным положением судна.
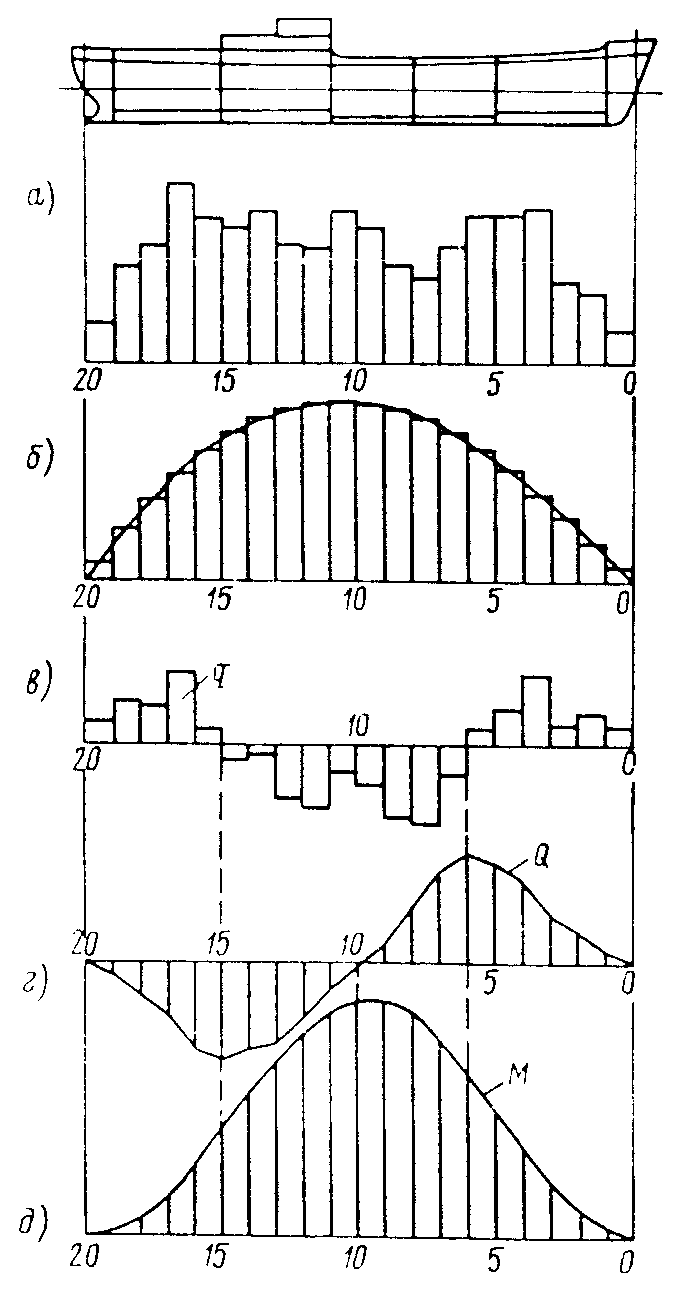
Рис. 7.1. Эпюры сил веса (а), сил плавучести (б), нагрузки (в), перерезывающих сил (г)
и изгибающих моментов (д)
.
При плавании судна по взволнованной поверхности моря происходит непрерывное перераспределение сил плавучести по длине судна вследствие изменения профиля волновой ватерлинии в процессе поступательного перемещения (хода) и качки судна. В результате такого перераспределения возникает дополнительная внешняя нагрузка на корпус судна, которая приводит к возникновению дополнительных перерезывающих сил и изгибающих моментов.
В результате килевой и вертикальной качки судна возникают также дополнительные ускорения, а, следовательно, изменяются и силы веса. Кроме того, в условиях такой качки при ходе против встречной волны происходит периодическое оголение носовой оконечности судна; при входе ее в воду на днище действуют значительные гидродинамические силы, вызывающие соответствующий динамический изгиб корпуса судна.
В классической теории общего продольного изгиба корпуса судна на волнении обычно принимают допущение, что с точки зрения общей продольной прочности наиболее неблагоприятными являются такие положения судна, когда его мидель-шпангоут располагается либо на вершине, либо на подошве волны, гребень которой перпендикулярен ДП судна, а длина равна длине судна (рис.7.2.). Если средняя часть судна находится на вершине волны (рис.7.2.а), то силы плавучести на этом участке возрастают, а к оконечностям убывают. В этом случае корпус судна изгибается, получая перегиб. Наоборот, когда средняя часть судна находится на подошве волны (рис.7.2.б), силы плавучести посредине уменьшаются, а к оконечностям возрастают и судно получает прогиб.
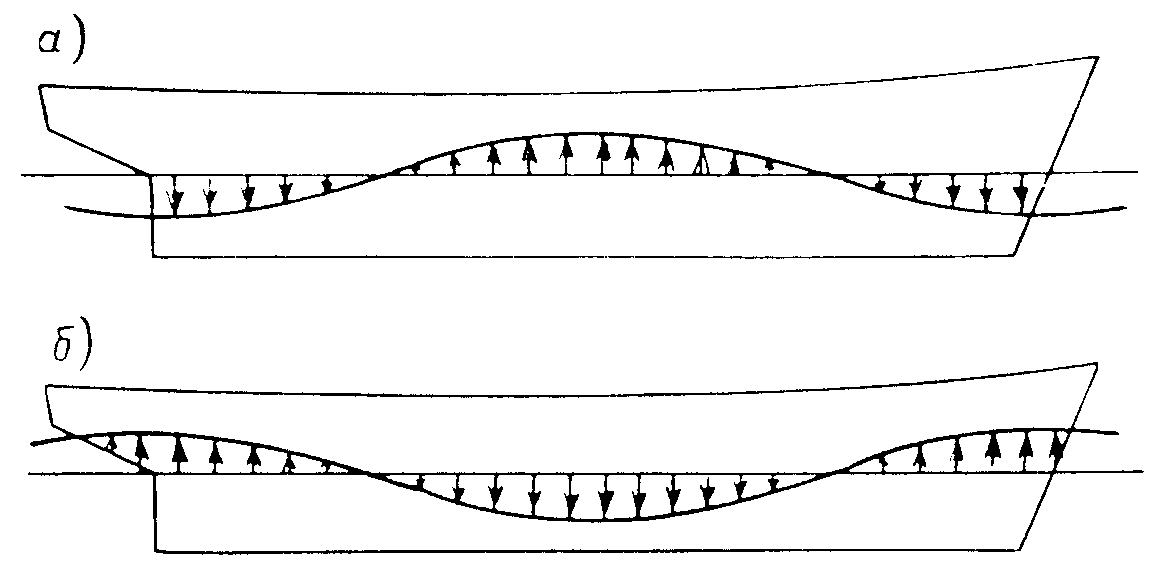
Рис. 7.2. Судно на вершине (а) и на подошве (б) волны
В тех случаях, когда гребень волны не перпендикулярен ДП судна, его корпус кроме общего продольного изгиба подвергается скручиванию. Однако скручивание, как правило, не является лимитирующим фактором для морских транспортных судов за исключением судов некоторых конструктивных типов, например судов открытого типа (с широкими люками). Для таких судов существует специальная расчетная методика.
Нормальные и касательные напряжения в продольных связях корпуса.
С достаточной для практических целей точностью можно принять, что деформация общего изгиба корпуса судна как тонкостенной пустотелой составной балки следует гипотезе плоских сечений и подчиняется общепринятой теории изгиба балок. Согласно этой теории нормальные напряжения в поперечных сечениях по высоте балки изменяются по линейному закону, а по ширине балки остаются неизменными для каждого отстояния от нейтральной оси сечения (проходящей через его ЦТ). Таким образом, нормальные σ и касательные τ напряжения в продольных связях корпуса могут быть определены по известным формулам:
s = M*zi / I
t = Q*S / (I*b)
где М – изгибающий момент, действующий в рассматриваемом поперечном сечении;
zi, – отстояние ЦТ поперечного сечения данной продольной связи от нейтральной оси;
I – момент инерции площади поперечного сечения продольных связей корпуса относительно нейтральной оси;
Q – перерезывающая сила в поперечном сечении;
S – статический момент относительно нейтральной оси части площади поперечного сечения продольных связей, расположенной выше или ниже горизонтального сечения, в котором определяются касательные напряжения;
b – суммарная толщина продольных связей корпуса, пересекаемых горизонтальным сечением, на уровне которого определяются касательные напряжения.
Дата добавления: 2017-03-12; просмотров: 5390;











