Выбор порога в алгоритме классификации (7)
Выражение (7) представляет собой детерминированный аналог стохастического алгоритма классификации, где 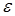 рассматривается как выборочное среднее стационарного случайного процесса. В изложенной выше постановке
рассматривается как выборочное среднее стационарного случайного процесса. В изложенной выше постановке 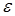 можно трактовать как сглаженное значение процесса
можно трактовать как сглаженное значение процесса 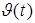 , поэтому
, поэтому 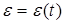 . Так как система (1), (2) является детерминированной, то подход, предложенный для стохастических систем, не применим.
. Так как система (1), (2) является детерминированной, то подход, предложенный для стохастических систем, не применим.
Предлагаемый ниже метод определения функции 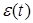 основан на многократном сглаживании сигналов. Сначала находится предварительная оценка
основан на многократном сглаживании сигналов. Сначала находится предварительная оценка 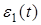 порога
порога 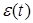 путем пропускания сигнала
путем пропускания сигнала 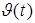 через сглаживающий фильтр
через сглаживающий фильтр
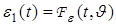 ,
,
где 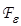 — оператор сглаживания.
— оператор сглаживания.
Для принятия решения о применении 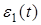 в качестве пороговой функции в алгоритме (7) необходимо ввести некоторый критерий. Для этого сформируем функцию
в качестве пороговой функции в алгоритме (7) необходимо ввести некоторый критерий. Для этого сформируем функцию 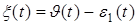 , которую пропустим через сглаживающий фильтр с оператором
, которую пропустим через сглаживающий фильтр с оператором 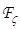 . В результате получим сигнал
. В результате получим сигнал 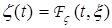 , который представляет собой ошибку работы фильтра
, который представляет собой ошибку работы фильтра 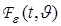 (в статистической теории в качестве критерия применяют вероятность ложных тревог). Далее определяем величину
(в статистической теории в качестве критерия применяют вероятность ложных тревог). Далее определяем величину 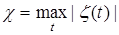 и проверяем условие (критерий):
и проверяем условие (критерий):
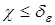 , (10)
, (10)
где 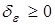 — некоторое число.
— некоторое число.
Если условие (10) выполняется, то полагаем 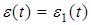 , в противном случае производим коррекцию функции
, в противном случае производим коррекцию функции 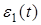 . Введем переменную
. Введем переменную
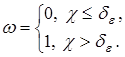
Тогда для 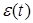 получим
получим
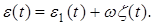
Заметим, что при неудачном выборе фильтра 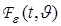 или
или 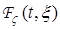 описанная процедура может повторяться до тех пор, пока не будет выполняться (10).
описанная процедура может повторяться до тех пор, пока не будет выполняться (10).
Схема системы идентификации параметрических ограничений показана на рис. 1.
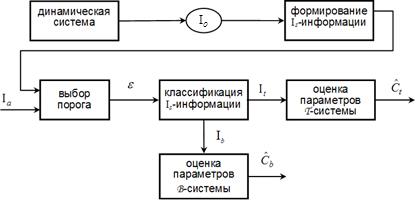
Рис. 1. Схема системы идентификации параметрических ограничений
| Замечание | |
| @ | Описанная процедура определения порога может применяться для оценки математического ожидания нестационарных стохастических процессов. |
1.4. Адаптивные алгоритмы оценивания параметров
T- и B-систем
Для идентификации параметров T-системы применим модель
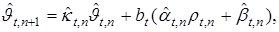 (11)
(11)
где 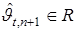 — прогноз выхода T-системы;
— прогноз выхода T-системы; 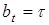 ;
; 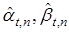 — оценки параметров T-системы.
— оценки параметров T-системы.
Заметим, что это одна из возможных моделей для оценки ограничений. Выбор ее структуры обусловлен упрощением реализации и необходимостью обеспечения мажорирующих свойств. Так как априори число 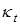 в (8) неизвестно, то предлагается получать его значение в процессе адаптации.
в (8) неизвестно, то предлагается получать его значение в процессе адаптации.
Запишем уравнение для ошибки прогнозирования выхода T-системы:
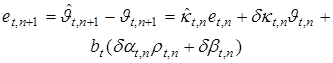 , (12)
, (12)
где 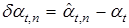 ,
, 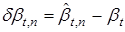 . Обозначим
. Обозначим 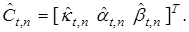 Тогда для настройки вектора параметров модели (11) применим алгоритм
Тогда для настройки вектора параметров модели (11) применим алгоритм
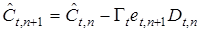 , (13)
, (13)
где 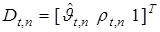 ,
, 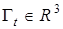 — диагональная матрица с
— диагональная матрица с 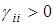 .
.
Оценивать параметры B-системы будем с помощью модели
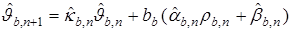 . (14)
. (14)
Алгоритм адаптации вектора 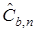 имеет вид
имеет вид
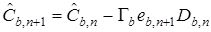 , (15)
, (15)
где 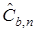 ,
, 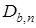 и
и 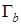 имеют тот же смысл, что и соответствующие векторы в (13).
имеют тот же смысл, что и соответствующие векторы в (13).
Правило останова адаптивных алгоритмов имеет вид
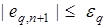 ,
,
где 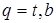 ,
, 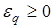 .
.
Дата добавления: 2017-02-13; просмотров: 1137;











