Инерционные динамические модели

Из всего разнообразия динамических моделей с «памятью» рассмотрим только те, которые имеют параметрическое представление. Основным представителем этого класса уравнений являются модели, описываемые обыкновенными дифференциальными уравнениями. 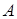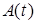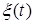Последние могут быть линейными или нелинейными как по параметрам, так и переменным; стационарными и нестационарными по , одномерными и многомерными; стохастическими, если вектор или носят случайный характер, и детерминированными.

Множество динамических процессов в объектах управления можно описать с помощью дифференциального уравнения с одним входом и выходом

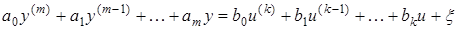. (1.7)

Из (1.7) можно получить операторное представление объекта через передаточную функцию.

От уравнения (1.7) нетрудно перейти к конечно-разностному представлению. Полагая 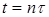, где 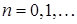, 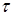— интервал съема данных, и вводя оператор 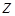сдвига назад

,

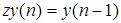получим

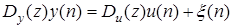, (1.8)

где , .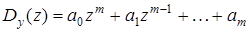

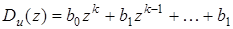Если 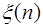случайная последовательность, то (1.8) представляет собой уравнение авторегрессии-скользящего среднего, а при 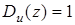— модель скользящего среднего. В общем случае уравнение авторегрессии-скользящего среднего с динамической спецификацией для 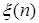имеет вид (1.3).

Уравнения (1.7)–(1.8) можно записать в матричной форме (в форме Коши или в пространстве состояний). Такое представление в связи с применением в системах управления средств вычислительной техники в настоящее время является общепринятым. Для линейного стационарного объекта уравнение в пространстве состояний имеет вид

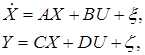(1.9)

где 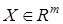— вектор состояния, 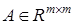— матрица состояния, 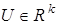— вектор входа, 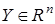— вектор выхода, , , 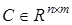, 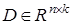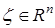— ненаблюдаемый вектор ошибок измерения, 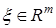— вектор помех.

Матрицы 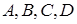параметризованы с точностью до некоторых векторов 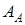, , 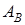, 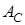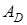. Первое уравнение в (1.9) называют уравнением состояния, а второе — уравнением измерения (наблюдения). В задачах идентификации матрица 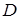обычно является нулевой.

Аналогичные модели состояния могут быть получены для нестационарных, нелинейных и дискретных объектов. Если 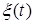является белым шумом, то первое уравнение в (1.9) можно рассматривать как стохастическое дифференциальное уравнение в форме Ито.

Реализация моделей в пространстве состояний связана с необходимостью оценки ненаблюдаемых компонентов вектора 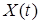на множестве 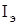. Часто это сказывается на процессе синтеза и свойствах алгоритмов адаптации и управления. Для преодоления указанных трудностей применяются модели с обобщенным входом (наблюдатели). В этом случае уравнение (1.9) приводится к так называемой идентификационной форме [78], позволяющей использовать информацию о входе и выходе объекта. Для объекта с одним входом 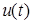и выходом 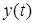модель с обобщенным входом записывается в виде

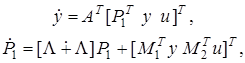(1.10)

где 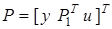— вектор обобщенного входа, 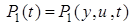, 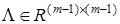— диагональная устойчивая матрица, 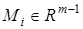( 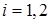) — вектор с постоянными параметрами, выбираемый так, чтобы пара ( 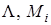) была наблюдаемой, 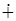— знак прямой суммы матриц, 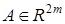— вектор параметров.

Уравнению (1.10) соответствует одно из представлений объекта в пространстве состояний, получившее название неявной идентификационной формы. В общем виде уравнение (1.10) может содержать вектор обратной связи, зависящий от 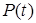. В этом случае можно получить каноническое (явное) идентификационное представление в пространстве состояний. В дискретном случае (1.10) соответствует разностное уравнение с обобщенным входом. В общем случае дискретные модели с обобщенным входом можно привести к (1.5).

Рассмотренные уравнения являются основой настраиваемых моделей, применяемых в системах идентификации и управления. Настраиваемая модель должна в каждый момент времени 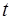вырабатывать прогноз выходной величины объекта на основе текущего множества экспериментальных данных. Поэтому настраиваемую (адаптивную) модель часто называют прогнозирующей. Близость параметров модели к параметрам объекта служит признаком правильной (адекватной) работы модели.