На практике очень часто имеют дело с несколькими событиями, которые находятся между собой в некоторых отношениях. Поэтому рассмотрим эти различные отношения между событиями.

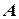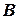Совмещением (или произведением) двух событий и называется событие, состоящее в совместном наступлении как события 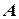, так и события 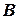. Это событие будем обозначать 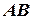или .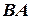

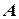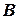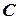Аналогично, совмещением нескольких событий, например , и , называется событие 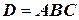, состоящее в совместном наступлении событи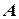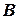й , и .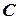

Объединением (или суммой) двух событи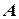й и 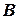называется событие 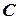, заключающееся в том, что произойдет по крайней мере одно из событи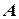й или 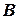. Это событие обозначается так: .

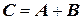Объединением нескольких событий называется событие, состоящее в появлении по крайней мере одного из них. Запись D=A+B+C означает, что событие D есть объединение событий A, В и С.

Два события A и В называются несовместными, если наступление события A исключает наступление события В. Отсюда следует, что если события A и Внесовместны, то событие AB— невозможное.

 

 

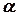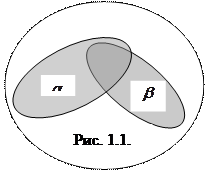
Рассмотрим следующий пример. Будем следить за движением какой-нибудь определенной молекулы газа, заключенного в некоторый объем. Внутри этого объема выделим объемы и 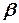, частично перекрывающие друг друга (рис. 1). Пусть событие A — попадание молекулы в объем 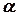, событие В — попадание молекулы в объем 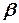. Совмещением событий A и В является попадание молекулы в общую часть объемов 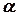и 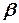. Если объемы 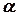и 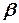не имеют общих точек, то ясно, что события A и Внесовместны. Объединением событий Aи В является попадание молекулы или только в объем 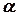или только в объем 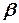, или же в их общую часть.


3. Аксиомы вероятностей.

Пусть A и B — два несовместных события, причем в n испытаниях событие A произошло 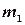раз, а событие В произошло 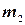раз. Тогда частоты событий A и В соответственно равны 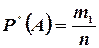, 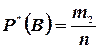. Так как события A и В несовместны, то событие A+B в данной серии опытов произошло 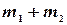раз. Следовательно,

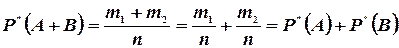
Таким образом, частота события A+B равна сумме частот событий A и В. Но при больших nчастоты P*(A), P*(B) и P*(A+B) мало отличаются от соответствующих вероятностей P(A), P(B) и P(A+B). Поэтому естественно принять, что если A и В — несовместные события, то

P(A+B)=P(A)+P(B).

Изложенное позволяет высказать следующие свойства вероятностей, которые можно принять в качестве аксиом.

 

Аксиома 1. Каждому случайному событию A соответствует определенное число Р(А), называемое его вероятностью и удовлетворяющее условию .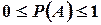

Аксиома 2. Вероятность достоверного события равна единице.

Аксиома 3 (аксиома сложения вероятностей). Пусть A и В — несовместные события. Тогда вероятность того, что произойдет хотя бы одно из этих двух событий, равна сумме их вероятностей:

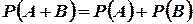(1.1)

Аксиома 3 допускает обобщение на случай нескольких событий, а именно: если события 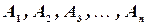, попарно несовместны, то

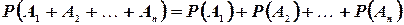(1.2)

Событием, противоположным событию 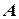, называется событие 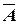, состоящее в ненаступлении события 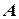. Очевидно, события 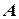и 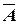несовместны.

Пусть, например, событие 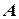состоит в том, что изделие удовлетворяет стандарту; тогда противоположное событие 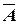заключается в том, что изделие стандарту не удовлетворяет. Пусть событие 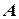- выпадение четного числа очков при однократном бросании игральной кости; тогда 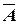— выпадение нечетного числа очков.

 

Теорема 1. Для любого события 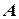вероятность противоположного события 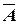выражается равенством

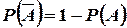(1.3)

Доказательство. Событие 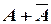, состоящее в наступлении или события 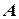, или события 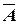, очевидно, является достоверным. Поэтому на основании аксиомы 2 имеем 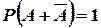. Так как события 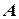и 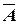несовместны, то используя аксиому 3, получим 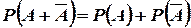. Следовательно, 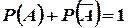, откуда .

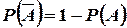Теорема 2. Вероятность невозможного события равна нулю.

Доказательство непосредственно следует из аксиомы 2 и теоремы 1, если заметить, что невозможное событие противоположно достоверному событию.

 

Дата добавления: 2017-02-13; просмотров: 1467;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, добавьте сайт познайка в закладки и расскажите о нем друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2025 год. Материал предоставляется для ознакомительных и учебных целей. Политика конфиденциальности
Генерация страницы за: 0.012 сек.