Постановка задачи синтеза.
При проектировании многопоточных планетарных механизмов необходимо, кроме требований технического задания, выполнять ряд условий связанных с особенностями планетарных и многопоточных механизмов. Задача проектирования и в этом случае может быть разделена на структурный и кинематический синтез механизма. При структурном синтезе определяется структурная схема механизма, при кинематическом – определяются числа зубьев колес, так как радиусы зубчатых прямо пропорциональны числам зубьев
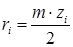
Для типовых механизмов первая задача сводится к выбору схемы из набора типовых схем. При этом руководствуются рекомендуемым для схемы диапазоном передаточных отношений и примерными оценками ее КПД. Для рассматриваемых схем эти данные приведены в таблице 17.1. После выбора схемы механизма необходимо определить сочетание чисел зубьев его колес, которые обеспечат выполнение условий технического задания - для редуктора это передаточное отношение и величина момента сопротивления на выходном валу. Передаточное отношение задает условия выбора относительных размеров зубчатых колес - чисел зубьев колес, крутящий момент задает условия выбора абсолютных размеров - модулей зубчатых зацеплений. Так как для определения модуля необходимо выбрать материал зубчатой пары и вид его термообработки, то на первых этапах проектирования принимают модуль зубчатых колес равным единице, то есть решают задачу кинематического синтеза механизма в относительных величинах.
При кинематическом синтезе (подборе чисел зубьев колес) задача формулируется так: для выбранной схемы планетарного механизма при заданном числе силовых потоков (или числе сателлитов k) и заданном передаточном отношении uнеобходимо подобрать числа зубьев колес zi, которые обеспечат выполнение ряда условий.
Условия подбора чисел зубьев. Вывод расчетных формул для условий соосности, соседства и сборки:
Условия, которые необходимо выполнить при подборе чисел зубьев колес типового планетарного механизма:
· заданное передаточное отношение с требуемой точностью
· соосность входного и выходного валов механизма
· свободное размещение (соседство) нескольких сателлитов
· сборку механизма при выбранных числах зубьев колес
· отсутствие подрезания зубьев с внешним зацеплением
· отсутствие заклинивания зубьев во внутреннем зацеплении
· минимальные относительные габариты механизма.
Рассмотрим эти условия подробнее на примере двухрядного планетарного механизма с одним внешним и одним внутренним зацеплением.
|
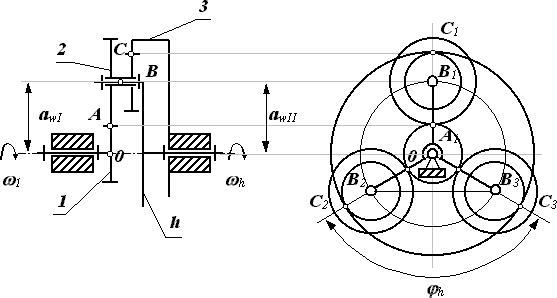
1. Обеспечение заданного передаточного отношения с требуемой точностью:
Принимаем требуемую точность ± 5%, тогда для рассматриваемой схемы механизма :
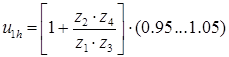
2. Обеспечение соосности входного и выходного валов:
Для этого необходимо чтобы межосевое расстояние в передаче внешнего зацепления (первый ряд) равнялось межосевому расстоянию в передаче внутреннего зацепления (второй ряд), то есть :
awI = awII ; awI= rw1 + rw2 = r1 + r2 ; awII = rw4 - rw3 = r4 - r3.
Обычно в планетарных механизмах применяются зубчатые колеса без смещения, для которых xi = 0и rwi = ri = zi  m / 2.
m / 2.
Тогда :
r1 + r2= r4 - r3 => mI  ( z1 + z2) = mII
( z1 + z2) = mII  (z4 - z3).
(z4 - z3).
Принимаем, что mI = mII = m, и получаем условие соосности для данной схемы механизма
| z1 + z2 = z4 - z3 |
3. Обеспечение условия соседства сателлитов (при числе сателлитов k > 1):
Сателлиты размещаются на окружности радиуса aw.Вершины зубьев сателлитов не будут мешать движению друг друга, если выполняется условие :
max ( da2,3 ) < lB2B3.
Для зубчатых колес без смещения ( ha*= 1, x2,3 = 0, 2 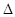 y = 0 ) максимальный из диаметров сателлитов равен
y = 0 ) максимальный из диаметров сателлитов равен
max ( da2,3 ) = max [( z2,3 + 2  ha* + 2
ha* + 2  x2,3 - 2
x2,3 - 2 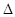 y)
y)  m ] = max[( z2,3 + 2)
m ] = max[( z2,3 + 2)  m ].
m ].
Расстояние между осями сателлитов :
lB2B3 = 2  aw
aw  sin ( jh / 2 ) = 2
sin ( jh / 2 ) = 2  (r1 + r2)
(r1 + r2)  sin ( p / k ). = (z1 + z2)
sin ( p / k ). = (z1 + z2)  m
m  sin ( p / k ).
sin ( p / k ).
Подставим полученные выражения в неравенство и получим условие соседства:
max [( z2,3 + 2)  m ] < (z1 + z2)
m ] < (z1 + z2)  m
m  sin (p / k).
sin (p / k).
| sin ( p /k ) > max [( z2,3 + 2)/ (z1 + z2) ] |
4. Обеспечить возможность сборки механизма с подобранными числами зубьев колес при заданном числе сателлитов k > 1:
Для вывода формулы условия сборки воспользуемся следующим методом:
Допустим, что все сателлиты устанавливаются на оси водила в одном и том же положении – точке В1. После установки первого сателлита, зубья колес z1и z4определенным образом установились относительно зубьев венцов сателлита. Тогда установить второй сателлит в этом же положении будет можно, если после поворота водила на угол 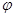 h колесо z1повернется на целое число угловых шагов В. При этом зубья колес z1и z4установятся относительно зубьев венцов сателлита так же, как и при установке первого сателлита.
h колесо z1повернется на целое число угловых шагов В. При этом зубья колес z1и z4установятся относительно зубьев венцов сателлита так же, как и при установке первого сателлита.
Угол поворота водила: 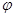 h= 2
h= 2 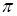 / k
/ k
Угловой шаг первого колеса: 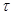 1 = 2
1 = 2 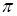 / z1
/ z1
Угол на который повернется первое колесо при повороте водила на угол 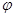 h :
h :
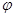 1 =
1 = 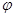 h
h  u1h =>
u1h => 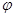 1 = 2
1 = 2 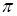
 u1h / k
u1h / k
Число угловых шагов 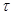 1в угле
1в угле 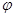 1 => B =
1 => B = 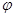 1 /
1 / 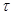 1, где B- произвольное целое число.
1, где B- произвольное целое число.
Подставляем все эти выражения в формулу для Bи после преобразований получаем :
2 
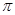 u1h
u1h  z1 / (k
z1 / (k  2
2 
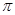 ) = B =>
) = B =>
u1h  z1 / k = B. z1 / k = B.
|
Поворачивать водило можно на угол jhплюс произвольное число pполных оборотов водила, то есть:
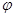 h= 2
h= 2 
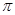 / k + 2
/ k + 2 
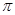
 р = 2
р = 2 
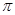 / k ( 1 + k
/ k ( 1 + k  р).
р).
С учетом этого, формула для условия сборки примет следующий вид:
| U1h * z1 / k ( 1 + k * р) = B. |
5. Обеспечить отсутствие подрезания колес с внешними зубьями зубьев:
Это условие обеспечивается, если для всех колес с внешними зубьями выполняется неравенство zi > zmin.
6. Обеспечить отсутствие заклинивания во внутреннем зацеплении:
Это условие для передачи внутреннего зацепления, состоящей из колес без смещения, можно обеспечить при выполнении следующих неравенств:
| z с внеш. зуб. > 20, z с внутр. зуб. > 85, zd = z с внутр. зуб - z с внеш. зуб. > 8. |
7. Обеспечить минимальные габариты механизма.
Для рассматриваемой схемы условие обеспечения минимального габаритного размера R можно записать так
R = min [ max ( z1 + 2  z2 ), (kK
z2 ), (kK  z4) ],где kK - коэффициент, учитывающий особенности конструкции зубчатого колеса с внутренними зубьями.
z4) ],где kK - коэффициент, учитывающий особенности конструкции зубчатого колеса с внутренними зубьями.
Дата добавления: 2017-02-13; просмотров: 1066;











