Элементы зубчатого колеса.
Цилиндрические зубчатые передачи.
Передача непрерывного прошения от одного вала к другому с заданным передаточным отношением чаще всего осуществляется с помощью зубчатых механизмов. Зубчатые механизмы получили очень широкое применение как в машиностроении, так и в приборостроении благодаря большой надежности и точности в воспроизведения заданного закона движения. Если оси вращения валов параллельны, то применяется цилиндрическая зубчатая передача, аксоидами колес которой являются цилиндры. Такая передача относится к категории плоских механизмов. В лекциях 14-16 излагаются основы синтеза цилиндрической зубчатой передачи по заданному передаточному отношению. Эти основы называются геометрическим расчетом зубчатой передачи.
Элементы зубчатого колеса.
Цилиндрические зубчатые передачи, как отмечалось ранее, могут быть внешнего и внутреннего зацеплений. Следует также указать реечное зацепление, разграничительное между внешним и внутренним зацеплениями. Простая зубчатая передача имеет два подвижных звена, которыми являются зубчатые колеса. Рассмотрим элементы зубчатого колеса (рис. 14.l).
|
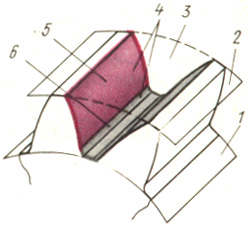 Поверхность (1), отделяющая зубья от тела зубчатого колеса, называется поверхностью впадин зубьев. Поверхность (2), ограничивающая зубья со стороны, противоположной телу зубчатого колеса, - поверхность вершин зубьев. Пространство между двумя соседними зубьями (3) - впадина. Поверхность, ограничивающая зуб со стороны впадины (4), называется боковой поверхностью зуба.
Поверхность (1), отделяющая зубья от тела зубчатого колеса, называется поверхностью впадин зубьев. Поверхность (2), ограничивающая зубья со стороны, противоположной телу зубчатого колеса, - поверхность вершин зубьев. Пространство между двумя соседними зубьями (3) - впадина. Поверхность, ограничивающая зуб со стороны впадины (4), называется боковой поверхностью зуба.
Боковая поверхность состоит из главной (5) и переходной (6) поверхностей. Главная поверхность - это та часть боковой поверхности зуба, которая, взаимодействуя с главной поверхностью другого зуба, обеспечивает заданное передаточное отношение. Переходная поверхность соединяет главную поверхность с поверхностью впадин.
Главной поверхностью чаще всего является эвольвентная поверхность. так как среди цилиндрических передач особое распространение получили эвольвентные цилиндрические передачи. Объясняется это тем, что они имеют весьма значительные преимущества перед другими передачами. Так, эвольвентные передачи допускают, в определенных пределах, изменение межосевого расстояния, сохраняя при этом постоянство передаточного отношения, чего другие передачи не допускают, и обладают хорошими эксплуатационными качествами. Изготовление эвольвентных колес и инструмента для их нарезания является наиболее простым, что имеет очень важное практическое значение.
|
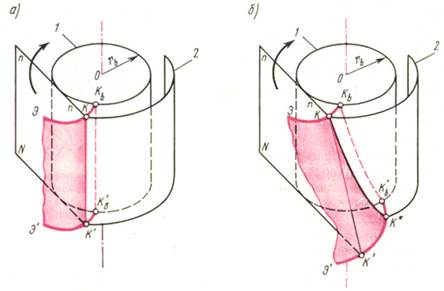 Рассмотрим образование эвольвентных поверхностей, которые будут являться главными поверхностями прямого и косого зубьев. На рис. 14.2, а в перспективе показана главная поверхность прямого зуба, которую можно представить как совокупность совершенно одинаковых эвольвент (Э, Э'), расположенных в плоскостях, перпендикулярных оси колеса. Эти эвольвенты являются траекториями точек образующей прямой КК', принадлежащей плоскости N, которая перекатывается по основному цилиндру 1 без скольжения. Начальные точки всех эвольвент распола-гаются на образующей KbKb’ основного ци-линдра. Пересечение главной поверхности прямого зуба с любым соосным цилиндром 2 происходит по образующей этого цилиндра (например, прямая КК'). Эта прямая параллельна оси колеса и называется линией прямого зуба. Главная поверхность прямого зуба является эвольвентной линейчатой цилиндрической поверхностью.
Рассмотрим образование эвольвентных поверхностей, которые будут являться главными поверхностями прямого и косого зубьев. На рис. 14.2, а в перспективе показана главная поверхность прямого зуба, которую можно представить как совокупность совершенно одинаковых эвольвент (Э, Э'), расположенных в плоскостях, перпендикулярных оси колеса. Эти эвольвенты являются траекториями точек образующей прямой КК', принадлежащей плоскости N, которая перекатывается по основному цилиндру 1 без скольжения. Начальные точки всех эвольвент распола-гаются на образующей KbKb’ основного ци-линдра. Пересечение главной поверхности прямого зуба с любым соосным цилиндром 2 происходит по образующей этого цилиндра (например, прямая КК'). Эта прямая параллельна оси колеса и называется линией прямого зуба. Главная поверхность прямого зуба является эвольвентной линейчатой цилиндрической поверхностью.
|
 Главная поверхность косого зуба (рис. 14.2, б) также может быть представлена как совокупность одинаковых эвольвент (Э, Э'), расположенных в плоскостях, перпендикулярных оси колеса; однако в этом случае образующая прямая КК' расположена на плоскости N под некоторым углом к оси колеса. Благодаря этому при перекатывании плоскости N по основному цилиндру 1 без скольжения начальные точки эвольвент располагаются по винтовой линии KbKb’ на основном цилиндре. В пересечении с любым соосным цилиндром 2 главная поверхность косого зуба образует винтовую линию КК*, называемую линией косого зуба. Главная поверхность косого зуба является эвольвентной линейчатой винтовой поверхностью.
Главная поверхность косого зуба (рис. 14.2, б) также может быть представлена как совокупность одинаковых эвольвент (Э, Э'), расположенных в плоскостях, перпендикулярных оси колеса; однако в этом случае образующая прямая КК' расположена на плоскости N под некоторым углом к оси колеса. Благодаря этому при перекатывании плоскости N по основному цилиндру 1 без скольжения начальные точки эвольвент располагаются по винтовой линии KbKb’ на основном цилиндре. В пересечении с любым соосным цилиндром 2 главная поверхность косого зуба образует винтовую линию КК*, называемую линией косого зуба. Главная поверхность косого зуба является эвольвентной линейчатой винтовой поверхностью.
Таким образом, основное сходство главных поверхностей прямого и косого зубьев состоит в том, что в любом торцовом сечении, т. е. в сечении плоскостью, перпендикулярной оси колеса, они имеют эвольвенту.
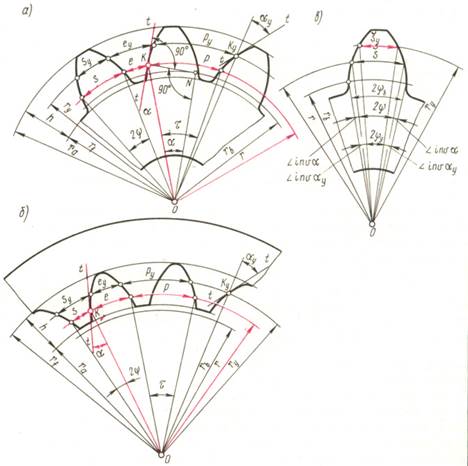
На рис. 14.3, а изображено зубчатое колесо с внешними зубьями. Наибольший радиус ra имеет окружность вершин. На рис. 14,3. б изображено зубчатое колесо с внутренними зубьями. В этом случае тело колеса имеет форму кольца, внутрь полости которого зубья обращены своими вершинами. Поэтому радиус ra окружности вершин внутренних зубьев меньше радиуса rf окружности впадин, который является, таким образом, наибольшим. На рис. 14.3 изображены также эвольвентный профиль зуба, основная окружность, на базе которой он построен (радиус rb), а также делительная окружность радиуса г и окружность произвольного радиуса ry.
На рис. 14.З буквой  обозначен
обозначен 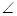 KON, равный углу профиля зуба в точке K, находящейся на делительной окружности прямозубого колеса. Этот угол стандартизован и равен 20°. Таким образом, делительная окружность прямозубого колеса является той окружностью, которая пересекает профиль зуба в точке, для которой угол профиля равен стандартному углу
KON, равный углу профиля зуба в точке K, находящейся на делительной окружности прямозубого колеса. Этот угол стандартизован и равен 20°. Таким образом, делительная окружность прямозубого колеса является той окружностью, которая пересекает профиль зуба в точке, для которой угол профиля равен стандартному углу  =20°.
=20°.
Если длину окружностей - делительной, основной и произвольного радиуса - поделить на число зубьев z, то получим расстояния между профилями двух соседних зубьев, называемые шагом, т. е. получим шаг по делительной окружности р, шаг по основной окружности pb и шаг по окружности произвольного радиуса py. Дуги р, pb и py соответствуют одному и тому же угловому шагу 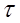 = p/r = pb/rb = py/ry. Отсюда следует, что шаги пропорциональны радиусам соответствующих окружностей. Угловой шаг можно выразить и так:
= p/r = pb/rb = py/ry. Отсюда следует, что шаги пропорциональны радиусам соответствующих окружностей. Угловой шаг можно выразить и так: 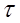 = 360°/z.
= 360°/z.
Важным элементом колеса является шаг по делительной окружности. Выразим длину делительной окружности через шаг р и число зубьев колеса z: 2 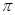 r = pz. Отсюда диаметр делительной окружности d = (p/
r = pz. Отсюда диаметр делительной окружности d = (p/ 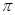 )*z = mz. Отношение p/
)*z = mz. Отношение p/ 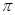 обозначают буквой m и называют модулем зубьев колеса (единица модуля - мм). Модуль стандартизован, причем стандарт предусматривает целый ряд значений модуля. Через модуль выражают радиус делительной окружности и все линейные размеры как колеса, так и передачи:
обозначают буквой m и называют модулем зубьев колеса (единица модуля - мм). Модуль стандартизован, причем стандарт предусматривает целый ряд значений модуля. Через модуль выражают радиус делительной окружности и все линейные размеры как колеса, так и передачи:
r = m*z/2; (14.1)
p = 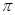 *m. (14.2)
*m. (14.2)
Радиус основной окружности находится из 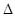 KON (рис. 14.3, а):
KON (рис. 14.3, а):
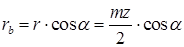 (14.3)
(14.3)
Радиус произвольной окружности колеса выражается следующим образом:
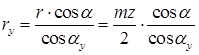 (14.4)
(14.4)
Так как шаги пропорциональны радиусам, то шаг по основной окружности:
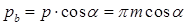
а шаг по окружности произвольного радиуса:
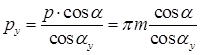 (14.5)
(14.5)
Основными параметрами колес являются модуль m и число зубьев z. Размеры делительных окружностей характеризуют размеры колес и передачи. Поскольку модуль определяется из прочностного расчета, а число зубьев назначает конструктор, то для уменьшения габаритов зубчатой передачи надо уменьшать числа зубьевее колес [см. уравнение (14.1]
Для колес с внутренними зубьями радиусы основной и делительной окружностей и шаги по этим окружностям определяют но тем же формулам, что и для колеса с внешними зубьями.
Шаг зубьев колеса по любой окружности можно представить как сумму толщины зуба sy и ширины впадины ey, т. е.
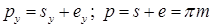
Колеса одного и того же модуля, имеющие одно и то же число зубьев, могут отличаться друг от друга толщиной зуба по делительной окружности.
Различают:
1) колеса с равноделенным шагом, у которых по делительной окружности толщина зуба равна ширине впадины и, следовательно, половине шага
s = e = 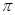 m/2;
m/2;
2) колеса, у которых s > е, т. е. s > 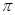 m/2;
m/2;
3) колеса, у которых s < е, т. е. s < 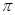 m/2.
m/2.
На рис. 14.3, в изображены центральные углы 2 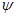 и 2
и 2 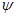 у, соответствующие дуговым толщинам зуба s и sу, а также эвольвентные углы inv
у, соответствующие дуговым толщинам зуба s и sу, а также эвольвентные углы inv  и inv
и inv  y. Из рисунка следует:
y. Из рисунка следует:
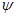 b =
b = 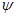 + inv
+ inv  =
= 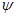 y + inv
y + inv  y
y
отсюда
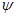 y =
y = 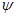 + inv
+ inv  - inv
- inv  y
y
Выражая угловые толщины через линейные 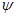 y = sy/(2ry)и
y = sy/(2ry)и 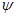 = s/(2r)и подставляя из значения в уравнение, ранее составленное для
= s/(2r)и подставляя из значения в уравнение, ранее составленное для 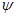 y, получим формулу для определения толщины внешнего зуба:
y, получим формулу для определения толщины внешнего зуба:
sy = ry (s/r + 2inv  - 2 inv
- 2 inv  y)(14.6)
y)(14.6)
Аналогично составляется формула для определения толщины sy внутреннего зуба:
sy = ry (s/r - 2inv  + 2 inv
+ 2 inv  y)
y)
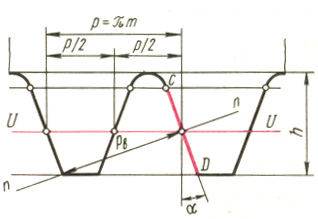 Если безгранично увеличивать число зубьев колеса, а следовательно, и радиусы всех окружностей, то в пределе при z=
Если безгранично увеличивать число зубьев колеса, а следовательно, и радиусы всех окружностей, то в пределе при z= 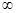 все окружности преобразуются в параллельные прямые, а эвольвентный профиль зуба станет прямолинейным, что имеет очень важное практическое значение. При z=
все окружности преобразуются в параллельные прямые, а эвольвентный профиль зуба станет прямолинейным, что имеет очень важное практическое значение. При z= 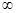 получим зубчатую рейку (рис. 14.4). В любом месте прямолинейной части зуба рейки профильный угол будет одним и тем же, равным
получим зубчатую рейку (рис. 14.4). В любом месте прямолинейной части зуба рейки профильный угол будет одним и тем же, равным  .
.
|
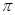 m. Шаг рейки, замеренный по нормали n-n к ее профилю, равен
m. Шаг рейки, замеренный по нормали n-n к ее профилю, равен 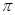 mcos
mcos  , т.е. равен шагу рb по основной окружности колеса, модуль которого такой же, как и модуль рейки.
, т.е. равен шагу рb по основной окружности колеса, модуль которого такой же, как и модуль рейки.
Дата добавления: 2017-02-13; просмотров: 3581;











