Реечное станочное зацепление.

Способы изготовления зубчатых колес. В настоящее время зубчатые колеса изготавливают способами ко­пирования и огибания.

По первому способу изготовляют зубчатые колеса в основном только с равноделенным шагом. При этом большинство их вы­полняется с заведомой погрешностью. Второй способ - способ огибания такими существенными недостатками не обладает: этим спо­собом можно изготовить самые разнообразные зубчатые колеса и притом теоретически точно. Поэтому способ огибания нашел распространение и представляет особый интерес.

При способе огибания заготовке, из которой изготовляют зуб­чатое колесо, и режущему инструменту, имеющему зубчатую форму (червячная фреза, гребенка, долбяк), сообщают на станке такие движения относительно друг друга, которые воспроизводят процесс зацепления. Это зацепление называют станочным.

Помимо движений, воспроизводящих процесс зацепления ин­струменту сообщается еще технологическое движение резания. При этом режущие кромки инструмента описывают по­верхность, называемую производящей. Укажем, что производящая поверхность и изготавливаемая боковая поверхность зуба являются взаимоогибаемыми, откуда сам способ и получил свое наименование.

При расчете геометрических параметров элементов высшей кинематической пары учитывают технологиче­ские возможности изготовления деталей на формообразующих станках (металлорежущих, прокатных станах, прессах и т. д.). Геометрия соответствующего формообразующего инструмента тес­ным образом связана с производящими поверхностями. Для инструментов, осуществляющих процесс формообразова­ния путем срезания стружки, такой производящей поверхностью является воображаемая поверхность, содержащая режущие кромки инструмента или образуемая при их главном движении, необходи­мом для резания. Если режущие кромки - прямые, а главное дви­жение - прямолинейное, то производящей поверхностью является плоскость. Если режущие кромки криволинейные, а главное дви­жение - прямолинейное, то производящей поверхностью является цилиндрическая поверхность (например, эвольвентная поверхность для долбяков).

Зацепление проектируемой поверхности зубьев с производящей поверхностью по аналогии с зацеплением нарезаемого колеса с производящей поверхностью режущего инструмента называют станочным зацеплением. Этот термин был предложен В. А. Гавриленко, крупным ученым, обобщившим и развившим основные положения теории зацепления эвольвентных передач. Сущность станочного зацепления заключается в том, что про­изводящая поверхность (поверхность режущих кромок инструмен­та) и проектируемая поверхность зуба («нарезаемого» колеса) имеют такое же относительное движение, какое имели бы зубчатые колеса при зацеплении друг с другом при взаимодействии аксоидных поверхностей.

При нарезании цилиндрических зубчатых колес оси произво­дящего колеса (т. е. воображаемого зубчатого колеса, у которого боковые поверхности являются производящими поверхностями) и проектируемого («нарезаемого») колеса параллельны между собой и аксоидами являются цилиндры. Если производящее колесо имеет конечное число зубьев, то режущими инструментами являются долбяк (рис. 14.5 е), абразивный хон (рис, 14.5 ж), которыми можно обрабатывать боковые поверхности зубьев колес с различными числами зубьев (рис, 14.5, з). При бесконечно большом ра­диусе аксоида производящего колеса инструмент должен иметь бесконечно большое число зубьев, т. е. превратиться в рейку. В этом случае инструментом обычно являются червячная фреза (рис. 14.5, б) или абразивный червячный круг (рис. 14.5, г), у ко­торых реечный производящий контур (рис. 14.5, д) расположен на винтовой поверхности. Частным случаем является инструмент, называемый зуборезной гребенкой (рис. 14.5, а) или пара тарельчатых шлифовальных кругов (рис. 14.5, в). Главным движением резания у долбяка, гребенки и абразивного хона является поступательное движение, а у червячной фрезы и

Рис 14.5

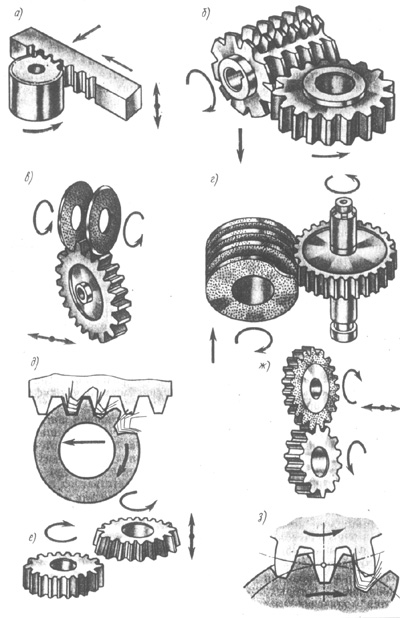шлифоваль­ных кругов - вращательное движение.

В процессе движения огибания (обкатки) основной шаг инстру­мента по профильной нормали соответствует основному шагу про­ектируемого («нарезаемого») колеса. Процесс перехода от формо­образования одного зуба к другому в процессе обкатки осуще­ствляется автоматически при непрерывном относительном движении (рис. 14.5, д. з).

Если производящую поверхность рассечь плоскостью, перпен­дикулярной оси нарезаемого колеса, то в сечении получим ис­ходный производящий контур (ИПК). Станочное зацепление есть зацепление ИПК с профилем зуба нарезаемого колеса.

Рассмотрим реечное станочное зацепление, т. е. такое, когда ИПК имеет очертания зубчатой рейки. Эвольвентные кромки это­го ИПК прямолинейны. Режущий инструмент (чер­вячная фреза или гребенка), образующий своим главным движени­ем эвольвентный реечный ИПК, обладает очень ценным свойством: его можно изготовить, сравнительно дешево и точно. Геометрия зубьев нарезаемого колеса определяется параметрами ИПК реечного инструмента и его расположением по отношению к колесу.

Исходный производящий контур эвольвентного реечного инстру­мента. Форма я размеры ИПК стандартизованы. Эвольвентные части профиля зубьев ИПК (рис. 14.6, а) прямолинейны и на­клонены к оси зуба под углом 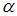. Переходы от прямолинейной части зуба к основанию впадины и к вершине осуществлены по дуге радиусом 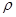_t. Точки сопряжения отмечены на ИПК буквами А, С, D, Е. Прямолинейная часть CD является эвольвентной, а скругления АС и DE - неэвольвентной частью контура. Прямая, разделяющая зуб по высоте на две равные части, называется делительной. На ИПК отмечаются еще четыре линии, параллельные делительной прямой и проходящие по основаниям впадин зубьев, по их вер­шинам и через точки сопряжения С и О. Расстояния между этими прямыми выражают размеры зуба исходного производящего кон­тура по высоте и измеряются соответственно величинами h_a = h_a^*m и C = c^*m, где h_a^* - коэффициент высоты зуба, с^* - коэффициент радиального зазора. Согласно стандарту: h_a^* = 1,0 ; с^* = 0,25. Прямые, проходящие через точки С и D, называются пря­мыми граничных точек.

Рис. 14.6

Размерами вдоль делительной прямой являются шаг, толщина зуба н ширина впадины. Шаг р исходного производящего контура, измеренный по любой прямой, параллельной делительной, есть ве­личина постоянная, равная 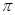m, где m - стандартный модуль. Тол­щина зуба ИПК по делительной прямом равна ширине впадины s₀ = e₀ = 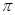m/2, а вместе они составляют шаг. Угол профиля зуба стандартизован: = 20°. Радиус скругления (дуги DE)

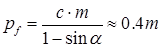(14.7)

Таким образом. ИПК реечного инструмента характеризуется четырьмя стандартными параметрами: m, , h_a^*, c^*.

Реечное станочное зацепление и коэффициент смещения. Рееч­ное станочное зацепление, как и всякое зацепление, имеет началь­ные линии. Ими являются станочно-начальная прямая рейки и станочно-начальная окружность колеса, которые катятся друг по другу без скольжения. Можно показать, что в реечном станочном зацеплении радиус r_w0 станочно-начальной окружности равен радиусу делительной окружности r.

Угол реечного станочного зацепления _w0 равен профильному углу а исходного производящего контура (как углы с взаимно перпендикулярными сторонами). Отметим также, что угол профиля зуба колеса в точке, находящейся на делительной окружности, равен профильному углу исходного производящего контура.

На станке инструмент можно расположить по-разному относи­тельно нарезаемого колеса. Поэтому в станочном зацеплении де­лительная прямая ИПК может располагаться различным образом по отношению к делительной окружности колеса: I) она может касаться делительной окружности - нулевая установка инструмен­та; 2) быть отодвинутой от нее — положительная установка; 3) пе­ресекать ее—отрицательная установка.

Расстояние между делительной прямой и делительной окруж­ностью называется смещением инструмента. Его выражают в виде произведения модуля m на коэффициент смещения х и ему присваивают знак. При нулевой установке смещение mх > 0, х > 0. При положительной установке mх > 0, х> 0. При отрицательной установке смещением является стрелка сегмента, которую делитель­ная прямая отсекает от делительной окружности; в этом случае mx < 0, x < 0.

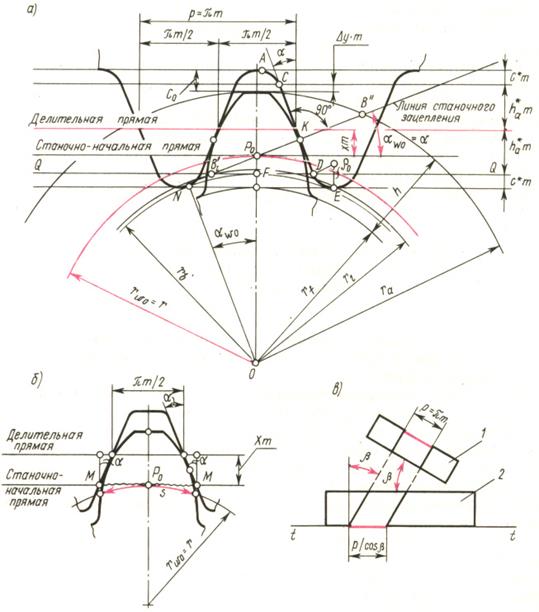
На рис. 14.6, а изображено реечное станочное зацепление при нарезании зубчатого колеса с положительным смещением и указаны все элементы производящего исходного контура, нарезаемого коле­са и станочного зацепления.

Линия реечного станочного зацепления начинается в точке N и через полюс P₀ уходит в бесконечность. Длина ее активной части ограничена точками В₁^’ и B^’’, находящимися на пересечении линии станочного зацепления с прямой QQ граничных точек и окруж­ностью вершин (рис. 14.6, а)

Профиль зуба колеса имеет эвольвентную и неэвольвентную части. Переход эвольвснтного профиля в неэпольвентиый находится на окружности граничных точек колеса, радиус которой r_l = OB₁^'.

Расстояние между окружностью вершин зубьев колеса и прямой впадин ИПК представляет собой станочный зазор С₀. Величина его складывается из двух частей: с^*m, 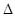ym, где 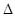у — коэффи­циент уравнительного смещения.

Размеры изготовляемого зубчатого колеса с внешними зубьями. Диаметр вершин прямозубого колеса (рис. 14.6, а):

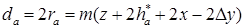(14.8)

Высота зуба из того же рисунка:

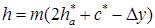(14.9)

Если x = 0 (смещения инструмента нет) и 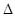у = 0, то d_a = m(z + 2h_a^*), h = m(2h_a^* + с^*), и при стандартных значениях h_a^* = 1,0 и с^* = 0,25 получим d_a = m(z+2) и h = 2,25m.

Стачочно-начальная прямая перекатывается по станочно-начальной окружности (она же делительная) без скольжения. По­этому толщина зуба s по делительной окружности нарезаемого колеса равна ширине ММ впадины по станочно-начальной прямой ИПК (рис. 14.6, б).

Отрезок ММскладывается из ширины впадины ИПК по де­лительной прямой e₀ = 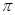m/2 и двух катетов, каждый из которых равен xm tg , поэтому:

s = 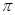m/2 + 2 xm tg (14.10)

Если инструмент установлен относительно колеса без смещения (xm = 0), то s = 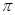m/2; значит, толщина зуба s по делительной ок­ружности колеса равна ширине впадины е, так как s + е = 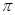m. В этом случае получается колесо с равноделенным шагом s = e, Если xm > 0, то s > 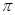m/2 и, следовательно, s > e. Если xm < 0, то s < 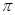m/2, и поэтому s < e.

При нарезании косозубых колес применяется тот же инструмент 1, что для прямозубых, но устанавливается он наклонно под углом 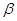по отношению к торцовой плоскости t - t колеса (заготовки) (рис. 14.6, в). На этом рисунке показана развертка 2 делительного цилиндра косозубого колеса, в результате чего винтовые линии косого зуба преобразо­вались в прямые линии. В торцовой плоскости t - t косозубого колеса вследствие наклона инструмента шаг увеличивается и становится равным p/cos 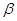, а следова­тельно, и модуль в торцовой плоскости будет нестандарт­ным, равным m/cos 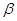. По­этому при расчете линейных размеров косозубого колеса по формулам, в которые входит стандартный модуль, вместо m следует подставлять m/cos 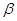, например делительный диаметр косозубого колеса d = zm/ cos .

Рис 14.7

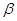Обратим внимание на размеры h_a^*m, c^*m, xm, 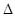y*m, перпенди­кулярные делительной прямой (рис. 14.6, а), которые принято назы­вать размерами по высоте. На рис. 14.6 в эти размеры расположены перпендикулярно плоскости рисунка. Поэтому при повороте инстру­мента на угол 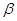размеры по высоте не изменяются. А отсюда следует, что когда в уравнениях встречаются произведения h_am, cm, xm, 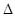ym, то их при расчете косозубой передачи можно под­ставлять в эти уравнения без всякого пересчета сомножителей. Так, например, формула диаметра вершин косозубого колеса может быть записана следующим образом: d_a = d + 2(h_a^*m + x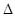m - y*m).

Угол профиля исходного производящего контура при нарезании косозубого колеса увеличивается по сравнению со стандартной величиной = 20°, поскольку размеры по высоте не изменяются, а шаг в торцовом сечении увеличивается. Расчетный угол профиля _t исходного производящего контура при нарезании косозубых ко­лес определяют по формуле:

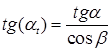
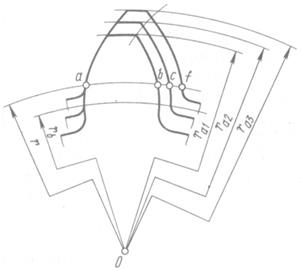
На рис. 14.7 сравниваются профили зубьев трех колес, имею­щих одинаковые числа зубьев, нарезанные одним и тем же ин­струментом, но с различными смещениями: x₁ < x₂ < x₃. Колеса имеют одинаковые радиусы делительных и основных окружностей; следовательно, профили зубьев всех трех колес очерчены по одной и той же эвольвенте. Но толщины зубьев s₁, (дуга ab), s₂ (дуга ас), s₃ (дуга af) и радиусы окружностей вершин r_a1, r_a2, r_a3, у колес будут разные. По мере увеличения х толщина зуба у основания увеличивается, а у вершины уменьшается, т. е. коэффициент сме­щения существенно влияет на форму зуба. Следовательно, назначая при проектировании тот или иной коэффициент смещения, можно влиять на форму зубьев колёс и на качество зубчатой передачи, наделяя её желательными свойствами.

Контрольные вопросы к лекции N14

1. Что называют зубчатым колесом?

2. Расскажите об основных элементах зубчатого колеса.

3. Запишите формулы окружного и углового шагов эвольвентного зубчатого колеса.

4. Какие методы изготовления зубчатых колёс Вы знаете?

5. В чём заключается сущность изготовления эвольвентных колёс методом огибания?

6. Дайте определение станочного зацепления.

7. Выведите формулы для определения основных размеров зубчатого колеса ( 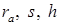) используя схему станочного зацепления.