Переходные процессы в цепях с одним реактивным элементом

Короткое замыкание в R-L цепи

На рис. 8.1 изображена электрическая цепь, в которой включен источник постоянной ЭДС. В результате коммутации рубильник замыкается и образуется замкнутый на себя R-L контур.

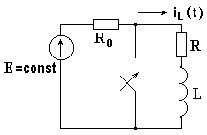До коммутации по индуктивности протекал ток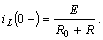

Этот ток создавал постоянное магнитное поле в индуктивной катушке.

Рис. 8.1

Определим закон изменения тока в индуктивности после коммутации.

В соответствии с классическим методом

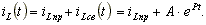
Принужденный ток после коммутации замыкается через рубильник, имеющий нулевое сопротивление, и через индуктивность не протекает. Индуктивный ток имеет только свободную составляющую

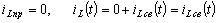
Магнитное поле, исчезая, индуктирует в индуктивной катушке ЭДС самоиндукции. Свободный ток в R-C контуре существует за счет этой электродвижущей силы.

Запишем уравнение для свободного тока в R-L контуре, используя второй закон Кирхгофа.

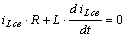(8.1)

Ищем решение этого уравнения в виде экспоненты

.

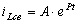Производная

.

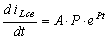Подставим значения свободного тока и производной тока в уравнение (8.1)

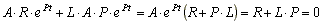(8.2)

Уравнение (8.2), полученное из уравнения (8.1), называется характеристическим.

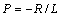- корень характеристического уравнения.

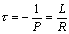- постоянная времени переходного процесса, измеряется в секундах.

Постоянная времени τ - это интервал времени, за который переходный ток уменьшается в e раз.

.

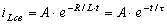Постоянную интегрирования А определяем с помощью начального условия.

В соответствии с первым законом коммутации,

.

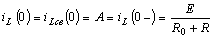Получим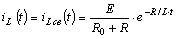

Напряжение на индуктивности

.

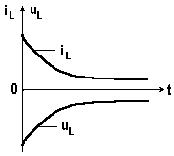
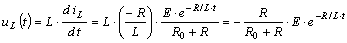На рис. 8.2 изображены кривые переходного тока в ветви с индуктивностью и переходного напряжения на индуктивности. Переходный ток и напряжение по экспоненте стремятся к нулю. В инженерных расчетах полагают, что через интервал времени, равный (4 ÷ 5)τ, переходный процесс заканчивается.

Рис. 8.2

Подключение R-L цепи к источнику постоянной ЭДС

В схеме на рис. 8.3 до коммутации рубильник разомкнут. В результате коммутации рубильник замыкается и подключает R-L цепь к источнику постоянной ЭДС. Определим закон изменения тока i(t).

.

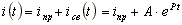Принужденный ток в установившемся режиме после коммутации

.

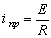В свободном режиме из схемы исключен внешний источник питания. Схема на рис. 8.3 без источника ЭДС ничем не отличается от схемы на рис. 8.1.

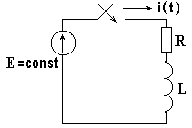Свободный ток определяется по формуле

.

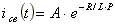Запишем значение переходного тока для момента коммутации, (t = 0). ,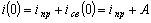

откуда .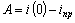

Рис. 8.3

До коммутации рубильник был разомкнут, и ток в схеме отсутствовал.

Сразу после коммутации ток в индуктивности остается равным нулю.

.

.

.

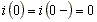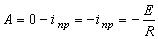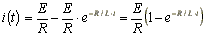Напряжение на индуктивности

.

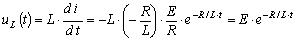На рис. 8.4 изображены кривые переходного, принужденного, свободного токов и переходного напряжения на индуктивности.

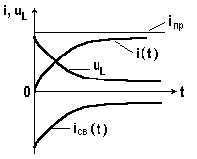Свободный ток и напряжение на индуктивности плавно уменьшаются до нуля. В момент коммутации свободный и принужденный токи одинаковы по абсолютной величине.

Переходный ток начинается при включении с нуля, затем возрастает, приближаясь к установившемуся постоянному значению.

Рис. 8.4

Короткое замыкание в R-C цепи

В схеме на рис. 8.5 в результате коммутации рубильник замыкается, и образуется замкнутый на себя R-C контур.

До коммутации емкость полностью зарядилась до напряжения, равного ЭДС источника питания, то есть u_c(0-) = E. После коммутации емкость полностью 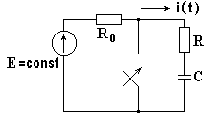разряжается, следовательно, принужденный ток в R-C цепи и принужденное напряжение на конденсаторе равны нулю.

В цепи существует только свободный ток за счет напряжения заряженного конденсатора.

Запишем для R-C контура уравнение по второму закону Кирхгофа .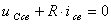

Рис. 8.5

Ток через конденсатор .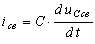

Получим дифференциальное уравнение

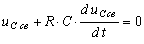. (8.3)

Решение этого уравнения .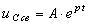

Подставим значение свободного напряжения и производной от напряжения

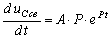в уравнение (8.3).

.

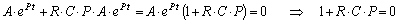Уравнение 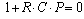называется характеристическим.

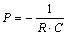- корень характеристического уравнения;

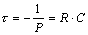- постоянная времени переходного процесса;

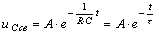
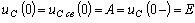
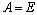
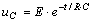
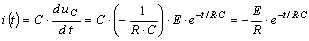
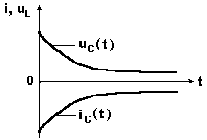Переходный ток и переходное напряжение на конденсаторе по показательному закону уменьшаются до нуля (рис. 8.6).

Рис. 8.6

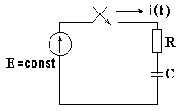
Подключение R-C цепи к источнику постоянной ЭДС

Полагаем, что до коммутации конденсатор не заряжен, напряжение на нем u_c(0-)=0.

В результате коммутации рубильник замыкается, и конденсатор полностью заряжается (рис. 8.7).

Принужденное напряжение на емкости равно ЭДС источника питания u_cпр= E.

Переходное напряжение

.

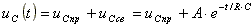В момент коммутации .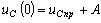

Постоянная интегрирования .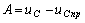

В соответствии со вторым законом

коммутации

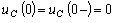
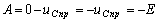
Рис. 8.7

Переходное напряжение

.

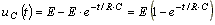Переходный ток

.

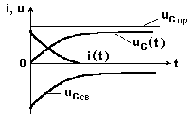
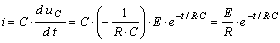Кривые напряжений и тока

изображены на рис. 8.8.

Рис. 8.8