Основные логические понятия, типовые логические функции и элементы (И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ, исключающее ИЛИ.

Элементы булевой алгебры

· Булевы константы («0» и «1»)

· Булевы переменные (Х1,Х2,…,Хn)Є{0,1}

· Булевы функции y=f(x1,x2,…,xn) принимают значения 0 и1

В отличие от переменной в обычной ал­гебре логическая переменная имеет толькодва значения, которые обычно называются логическим нулем и логической единицей. В качестве бозначений используются «О» и «1» или просто 0 и 1.

Существуют три основные операции между логическими переменными: конъюнкция (логическое умножение), дизъюнкция (логическое сложение) и ин­версия (логическое отрицание). По анало­гии с алгеброй чисел в алгебре логики ис­пользуются следующие обозначения опера­ций.

Конъюнкция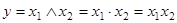

Дизъюнкция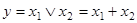

Инверсия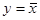

Применительно к логическим операциям существуют теоремы:

Коммутативный закон:

Ассоциативный закон:

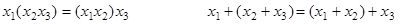
Дистрибутивный закон:

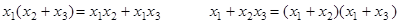
Правило склеивания:

Правило повторения:

Правило отрицания:

Правило двойного отрицания:

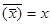
Теорема де Мограна:

Операции с нулем и единицей:

Таблицы истинности логических функций

Дизъюнкция (логическое сложение, ИЛИ)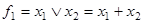

Конъюнкция (логическое умножение, И)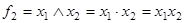

Равнозначность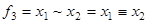

Импликация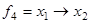

Функция Вебба (стрелка Пирса, ИЛИ-НЕ)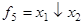

Функция Шеффера (И-НЕ)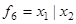

Функция сложения по модулю два (полусумматор)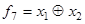

Как можно представить логические функции с помощью электрических переключающих схем? Так как логические переменные могут иметь только два дискретных значения, то следует обратить внимание на схемы, которые могут находиться в двух легко различимых рабочих состояниях. Простейшим способом реализации логической переменной является ключ.

Можно условиться, что разомкнутый ключ эквивалентен логическому нулю, а замк­нутый –логической единице. Таким обра­зом, ключ реализует переменную х, если он замкнут при х = 1, и переменную 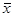, ес­ли он разомкнут при х = 1.

Рассмотрим сначала, какая логическая функция будет реализована, если два клю­ча 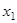и 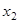соединить последовательно.

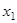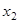Значение зависимой переменной у характеризуется тем, будет ли замкнута или разомкнута составная коммутируемая цепь, расположенная ме­жду входными клеммами. Очевидно, что рассматриваемая цепь будет замкнута только тогда, когда и замкнуты, т.е. равны единице. Таким образом, последова­тельное включение ключей реализует функ­цию И.

Функция ИЛИ может быть получе­на, если ключи включить параллельно.

С помощью такой схемной логики можно наглядно показать справедливость ранее приведенных теорем. Рассмотрим это на примере правила повторения.

На рис. показана реализация обеих частей выражения правила повторения с помощью коммутируе­мой цепи. Легко заметить, что рассматри­ваемое тождество выполняется, поскольку два включенных последовательно ключа, замыкание и размыкание которых проис­ходит одновременно, воздействуют на внешние цепи как один такой ключ.

Другой возможностью представления логических переменных является электри­ческое напряжение, имеющее два раз­личных уровня: высокий и низкий. Этим уровням можно поставить в соответствие логи­ческие состояния 1 и 0. Эта система обо­значений: высокий = 1 и низкий = 0 – на­зывается позитивной логикой. Но возмож­на также и обратная система обозначений: высокий = 0 и низкий = 1, которая назы­вается негативной логикой.

Основные логические функции могут быть реализованы с помощью соответ­ствующих электронных схем. Эти схемы имеют один или несколько входов и один выход. Как правило, они называются логи­ческими элементами. Уровень выходного напряжения определяется уровнями напря­жения на входах и характером логической функции. Для реализации одной и той же логической функции существует большое число различных электронных схем. По­этому с целью упрощения документации были введены символы, которые обозна­чают лишь только логическую функцию и не раскрывают внутреннее строение схемы.

В цифровой технике задача, как правило, формулируется в форме таблицы переключений, которая называется также таблицей истинности. Прежде всего требуется найти такую логическую функцию, которая соответствовала бы этой таблице. На следующем этапе эту функцию преобразуют в простейшую форму, которую потом реализуют с помощью соответствующей комбинации базовых логических схем. Логические функции записывают, как правило, в дизъюнктивной совершенной нормальной форме (ДСНФ). При этом поступают следующим образом.

1. В таблице истинности выделяют строки, в которых выходная переменная у имеет значение 1.

2. Для каждой такой строки составляют конъюнкцию всех входных переменно причем записывают сомножитель 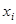, если рассматриваемая переменная принимает значение 1, в противном случае записывают 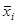. Таким образом, составляется столько произведений, сколько имеется строк с у = 1.

3. Наконец, записывая логическую сумму всех найденных произведений, получают искомую функцию.